目录

算法特点
这类算法的实质即为递归函数,DFS依据栈,BFS依据队列,最常见的是选数、走迷宫、棋盘类、多分支问题的求解,走迷宫常常会用偏移量数组,具体的如何偏移要结合题目进行具体分析,利用偏移量数组实现分支的规划与探索,最终求取答案。由于DFS与BFS均要结合具体问题具体实现,因此无固定模板,换句话说,这类题刷的多了也就知道怎么写了,培养思维是关键
Depth-First-Search
DFS全称为deep fast search,即深度优先搜索。产常用来求取一个问题是否有解、结合限制条件求取解决问题的方法总数、求取所有可行方法的具体情况,从某些元素当中选择元素实现目标。由于这样的问题往往繁琐复杂,以人的思维难以推算,这就需要我们利用计算机的思维,将方法思路告诉它,让它得到我们想要的正确结果。深度优先搜索其实质为递归函数,逐层递进,根据问题的要求决定是否回归,由于其过于暴力,所耗时间可能会使题目TLE,所以有时回归,有时则不回归。深度优先搜索所依据的另一个原理是栈的原理,即先入后出原则,一条路走到底。注意:BFS求解的答案一定是正确的,但是却不一定时最优(路径最短解)
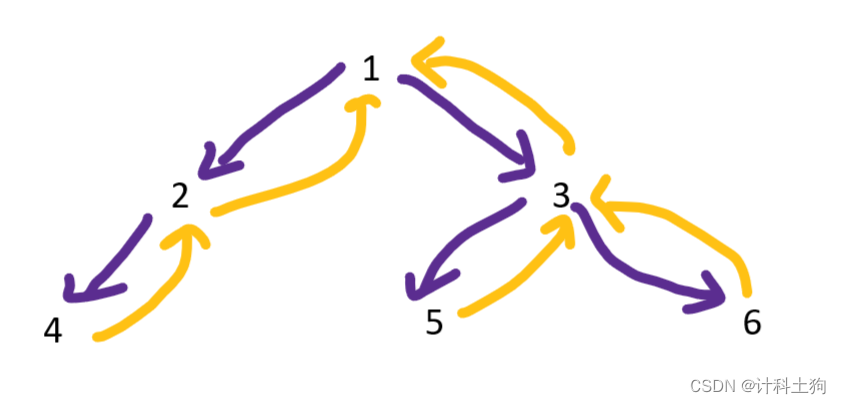
经典例题:上楼梯
题目描述
一个楼梯共有 n 级台阶,每次可以走一级或者两级或者三级,问从第 0 级台阶走到第 n 级台阶一共有多少种方案。
数据范围
1≤N≤20
输入
一个整数 N。
输出
一个整数,表示方案总数。
样例输入
4样例输出
7源代码
根据题目,我们可以知道从第0阶走到第n阶一共有三种分支,因此偏移量数组有了三个元素分别为1、2、3,对应着走一步、两步、三步。而后dfs是从第0阶开始搜索,当搜索到第n阶的时候证明此时有了一个解,因此全局变量ans ++ ,在DFS之中我们用到的常量除了参数外一般都要设置为全局变量以方便我们对于DFS函数之内的内部核心进行创建
#include <iostream>
using namespace std;
int ans = 0;
int n;
int dr[3] = {1,2,3};
void dfs(int u)
{
if(u == n)ans ++ ;
for(int i = 0;i < 3;i ++ )
{
int t = u + dr[i];
if(t >= 0 && t <= n)dfs(t);
}
}
int main()
{
cin >> n;
dfs(0);
cout << ans;
return 0;
}经典例题:排列数字
题目描述
给定一个整数 n,将数字 1∼n 排成一排,将会有很多种排列方法。现在,请你按照字典序将所有的排列方法输出。
输入
共一行,包含一个整数 n。
输出
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤7
输入样例
3输出样例
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1源代码
通过观察样例输出我们可以发现,在选数的同时,每种情况每个数只能选择一次,因此要开布尔数组进行回溯的准备,在对于偏移量数组进行枚举情况的同时,DFS回溯之后也要恢复现场,即布尔数组的0与1的转换,对于每种情况我们利用整型数组path来存储,当有解的时候输出此种情况即可
#include <iostream>
using namespace std;
const int N = 1000000+10;
bool vis[N];
int path[N];
int a[N];
int n;
void dfs(int u)
{
if(u == n)
{
for(int i = 0;i < n;i ++ )cout << path[i] << ' ';
cout << endl;
return;
}
for(int i = 1;i <= n;i ++ )
{
if(!vis[i])
{
vis[i] = 1;
path[u] = i;
dfs(u + 1);
vis[i] = 0;
}
}
}
int main()
{
cin >> n;
dfs(0);
return 0;
}经典例题:不同路径数
题目描述
给定一个 n×m 的二维矩阵,其中的每个元素都是一个 [1,9] 之间的正整数。
从矩阵中的任意位置出发,每次可以沿上下左右四个方向前进一步,走过的位置可以重复走。
走了 k 次后,经过的元素会构成一个 (k+1) 位数。
请求出一共可以走出多少个不同的 (k+1) 位数。
输入
第一行包含三个整数 n,m,k。
接下来 n 行,每行包含 m 个空格隔开的整数,表示给定矩阵。
输出
输出一个整数,表示可以走出的不同 (k+1) 位数的个数。
数据范围
对于 30% 的数据, 1≤n,m≤2,0≤k≤2
对于 100% 的数据,1≤n,m≤5,0≤k≤5,m×n>1
样例输入
3 3 2
1 1 1
1 1 1
2 1 1样例输出
5源代码
本题由于牵涉到了不重复情况n位数的去重和总数,可以使用vector库与algorithm库中的函数进行去重,为了避免因数据量过大出现的TLE情况,我们换一种库函数,利用哈希表进行处理,unordered_set库可以创建一个某种类型的数组,此数组可以自动进行去重运算,因此节省了大量的运算时间。至于走过的位置可以重复走就是告诉我们不必回溯和定义布尔数组,而后在此二维数组的每个元素位置都DFS搜索解,最后输出哈希表的大小即可
#include <iostream>
#include <unordered_set>
using namespace std;
const int N = 1000+10;
unordered_set<int> A;
int dx[4] = {-1,0,1,0};
int dy[4] = {0,-1,0,1};
int n,m,k;
int map[N][N];
void dfs(int x,int y,int u,int num)
{
if(u == k)A.insert(num);
else
{
for(int i = 0;i < 4;i ++ )
{
int X = x + dx[i];
int Y = y + dy[i];
if(X >= 1 && X <= n && Y >= 1 && Y <= m)
{
dfs(X,Y,u + 1,num * 10 + map[X][Y]);
}
}
}
}
int main()
{
cin >> n >> m >> k;
for(int i = 1;i <= n;i ++ )
{
for(int j = 1;j <= m;j ++ )
{
cin >> map[i][j];
}
}
for(int i = 1;i <= n;i ++ )
{
for(int j = 1;j <= m;j ++ )
{
dfs(i,j,0,map[i][j]);
}
}
cout << A.size();
return 0;
}经典例题:全排列英文
题目描述
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。我们假设对于小写字母有 a<b<…<y<z,而且给定的字符串中的字母已经按照从小到大的顺序排列。
输入
输入只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度在 1 到 6 之间。
输出
输出这个字符串的所有排列方式,每行一个排列。要求字母序比较小的排列在前面。
输入样例
abc输出样例
abc
acb
bac
bca
cab
cba提示
字母序如下定义:
已知 S=s1s2…sk,T=t1t2…tk,则 S<T 等价于,存在 p(1≤p≤k),使得 s1=t1,s2=t2,…,sp−1=tp−1,sp<tp 成立。
源代码
实质即为path数组换做char类型即可
#include <iostream>
using namespace std;
const int N = 1000000+10;
bool vis[N];
char path[N];
string s;
void dfs(int u)
{
if(u == s.size())
{
for(int i = 0;i < s.size();i ++ )cout << path[i];
cout << endl;
return;
}
for(int i = 0;i < s.size();i ++ )
{
if(!vis[i])
{
vis[i] = 1;
path[u] = s[i];
dfs(u + 1);
vis[i] = 0;
}
}
}
int main()
{
cin >> s;
dfs(0);
return 0;
}经典例题:走方格
题目描述
给定一个 n×m 的方格阵,沿着方格的边线走,从左上角 (0,0) 开始,每次只能往右或者往下走一个单位距离,问走到右下角 (n,m) 一共有多少种不同的走法。
输入
共一行,包含两个整数 n 和 m。
输出
共一行,包含一个整数,表示走法数量。
数据范围
0≤n,m≤10
样例输入
2 3样例输出
10源代码
两个分支,偏移量数组只有两个元素,注意布尔数组的标记与回溯恢复以及特判当n、m均为0时无解,输出0
#include <iostream>
using namespace std;
const int N = 1000+10;
bool vis[N][N];
int n,m;
int ans = 0;
int dx[2] = {0,1};
int dy[2] = {1,0};
void dfs(int x,int y)
{
if(x == n && y == m)
{
ans ++ ;
return;
}
for(int i = 0;i < 2;i ++ )
{
int X = x + dx[i];
int Y = y + dy[i];
if(X >= 0 && X <= n && Y >= 0 && Y <= m && !vis[X][Y])
{
vis[X][Y] = 1;
dfs(X,Y);
vis[X][Y] = 0;
}
}
}
int main()
{
cin >> n >> m;
if(n == 0 && m == 0)
{
cout << "0";
return 0;
}
dfs(0,0);
cout << ans;
return 0;
}经典例题:走出迷宫
题目描述
小明现在在玩一个游戏,游戏来到了教学关卡,迷宫是一个N*M的矩阵。小明的起点在地图中用“S”来表示,终点用“E”来表示,障碍物用“#”来表示,空地用“.”来表示。障碍物不能通过。小明如果现在在点(x,y)处,那么下一步只能走到相邻的四个格子中的某一个:(x+1,y),(x-1,y),(x,y+1),(x,y-1);小明想要知道,现在他能否从起点走到终点。
输入
本题包含多组数据。每组数据先输入两个数字N,M,接下来N行,每行M个字符,表示地图的状态。保证有一个起点S,同时保证有一个终点E.
输出
每组数据输出一行,如果小明能够从起点走到终点,那么输出Yes,否则输出No
数据范围
2<=N,M<=500
输入样例
3 3
S..
..E
...
3 3
S##
###
##E
输出样例
Yes
No源代码
注意数据过大,点不要重复走,否则会TLE时间超限
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 550;
int sx,sy,ex,ey,n,m,flag;
char map[N][N];
int dx[4] = {-1,0,1,0};
int dy[4] = {0,-1,0,1};
bool vis[N][N];
void dfs(int x,int y)
{
if(x == ex && y == ey)
{
flag = 1;
}
for(int i = 0;i < 4;i ++ )
{
int X = x + dx[i];
int Y = y + dy[i];
if(X >= 0 && X < n && Y >= 0 && Y < m && !vis[X][Y] &&map[X][Y] != '#')
{
vis[X][Y] = 1;
dfs(X,Y);
}
}
}
int main()
{
while(cin >> n >> m)
{
flag = 0;
memset(map,0,sizeof(map));
memset(vis,0,sizeof(vis));
for(int i = 0;i < n;i ++ )
{
for(int j = 0;j < m;j ++ )
{
cin >> map[i][j];
if(map[i][j] == 'S')
{
sx = i;
sy = j;
}
if(map[i][j] == 'E')
{
ex = i;
ey = j;
}
}
}
dfs(sx,sy);
if(flag == 1)cout << "Yes" << endl;
else if(flag == 0)cout << "No" << endl;
}
}Breadth-First-Search
BFS全称Breadth-First-Search,宽度优先搜索能够保证最优解的实现,也就是最短路,因此常常用来求取最短路径是多长和最优解。其搜索过程是逐层实现的,即一层一层的搜,当搜到某一层中有一个解的时候就会提前结束,也就不会再往下搜了。BFS实现的基础是queue库中的队列,不断的取头去头直至为空,答案就浮出水面了,步骤通常为一开始二标示三非空四取头五删头六标点七累加八推入
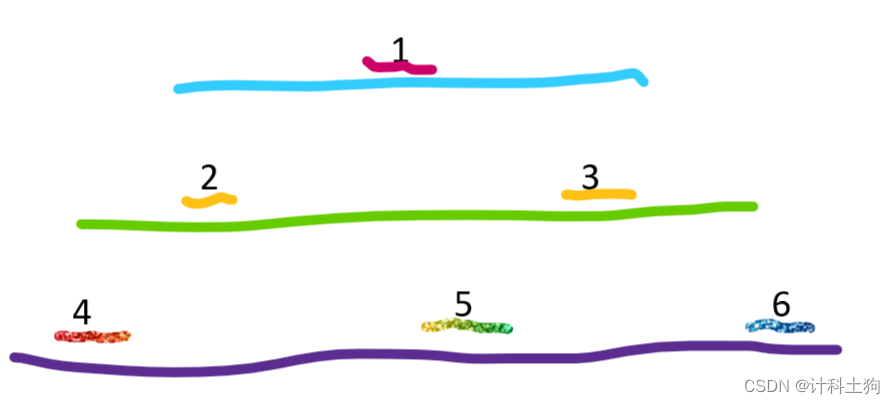
经典问题:走迷宫
题目描述
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0输出样例
8源代码
一般呢求取最短路径我们通常设置一个ans整型数组用于计数,此处的布尔数组仅仅是用来标记而不是回溯,BFS没有回溯仅仅把走过的路标记一下就可以,从某种方面来说也就是记忆路径,不走重复的路,减少数据的处理时间,从而达到最高的效率,对于队列的类型,在棋盘迷宫这类题型之中我们通常会设置一个结构体或者是typedef pair<int,int> PII,两种方式稍有不同,但目的相同
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 550;
int n,m;
int map[N][N];
int ans[N][N];
int dx[4] = {-1,0,1,0};
int dy[4] = {0,-1,0,1};
bool vis[N][N];
struct Point
{
int x;
int y;
};
queue<Point> A;
int bfs()
{
A.push({1,1});
vis[1][1] = 1;
while(!A.empty())
{
auto t = A.front();
A.pop();
for(int i = 0;i < 4;i ++ )
{
int X = t.x + dx[i];
int Y = t.y + dy[i];
if(X >= 1 && X <= n && Y >= 1 && Y <= m && !vis[X][Y] && map[X][Y] != 1)
{
vis[X][Y] = 1;
ans[X][Y] = ans[t.x][t.y] + 1;
if(X == n && Y == m)return ans[X][Y];
A.push({X,Y});
}
}
}
return ans[n][m];
}
int main()
{
cin >> n >> m;
memset(vis,0,sizeof(vis));
memset(ans,0,sizeof(ans));
for(int i = 1;i <= n;i ++ )
{
for(int j = 1;j <= m;j ++ )
{
cin >> map[i][j];
}
}
cout << bfs();
return 0;
}经典问题:地牢大师(三维最优解)
题目描述
你现在被困在一个三维地牢中,需要找到最快脱离的出路!地牢由若干个单位立方体组成,其中部分不含岩石障碍可以直接通过,部分包含岩石障碍无法通过。向北,向南,向东,向西,向上或向下移动一个单元距离均需要一分钟。你不能沿对角线移动,迷宫边界都是坚硬的岩石,你不能走出边界范围。请问,你有可能逃脱吗?如果可以,需要多长时间?
输入
输入包含多组测试数据。每组数据第一行包含三个整数 L,R,C 分别表示地牢层数,以及每一层地牢的行数和列数。接下来是 L 个 R 行 C 列的字符矩阵,用来表示每一层地牢的具体状况。每个字符用来描述一个地牢单元的具体状况。其中, 充满岩石障碍的单元格用”#”表示,不含障碍的空单元格用”.”表示,你的起始位置用”S”表示,终点用”E”表示。每一个字符矩阵后面都会包含一个空行。当输入一行为”0 0 0”时,表示输入终止。
输出
每组数据输出一个结果,每个结果占一行。如果能够逃脱地牢,则输出”Escaped in x minute(s).”,其中X为逃脱所需最短时间。如果不能逃脱地牢,则输出”Trapped!”。
数据范围
1≤L,R,C≤100
输入样例
3 4 5
S....
.###.
.##..
###.#
#####
#####
##.##
##...
#####
#####
#.###
####E
1 3 3
S##
#E#
###
0 0 0输出样例
Escaped in 11 minute(s).
Trapped!源代码
注意是三维哦!毕竟四维的层次不是我们
#include <iostream>
#include <queue>//queue
#include <cstring>//memset
using namespace std;
const int N = 110;
char map[N][N][N];//三维坐标系
bool vis[N][N][N];//标记数组
int ans[N][N][N];//最优解数组
//偏移量数组
int dx[6] = {0,0,1,0,-1,0};
int dy[6] = {0,0,0,1,0,-1};
int dz[6] = {1,-1,0,0,0,0};
//起始点坐标
int sx,sy,sz,ex,ey,ez;
//三维坐标点
struct Point
{
int x;
int y;
int z;
};
queue<Point> A;//三位点队列
int l,r,c;
int bfs()
{
A.push({sx,sy,sz});//推
vis[sx][sy][sz] = 1;//标记
while(!A.empty())//非空
{
auto t = A.front();//取头
A.pop();//删头
for(int i = 0;i < 6;i ++ )//开搜
{
int X = t.x + dx[i];
int Y = t.y + dy[i];
int Z = t.z + dz[i];
if(X >= 1 && X <= r && Y >= 1 && Y <= c && Z >= 1 && Z <= l && !vis[X][Y][Z] && map[X][Y][Z] != '#')
{
vis[X][Y][Z] = 1;//标记
ans[X][Y][Z] = ans[t.x][t.y][t.z] + 1;//答案累计
if(X == ex && Y == ey && Z == ez)return ans[X][Y][Z];//若搜到E提前结束
A.push({X,Y,Z});//入队
}
}
}
return ans[ex][ey][ez];//返回答案
}
int main()
{
while(cin >> l >> r >> c)
{
if(l == 0 && r == 0 && c == 0)break;
//因多实例输入,每次要重置数组内容
memset(map,0,sizeof(map));
memset(vis,0,sizeof(vis));
memset(ans,0,sizeof(ans));
//三维数组初始化
for(int k = 1;k <= l;k ++ )
{
for(int i = 1;i <= r;i ++ )
{
for(int j = 1;j <= c;j ++ )
{
cin >> map[i][j][k];
//起点坐标录入
if(map[i][j][k] == 'S')
{
sx = i;
sy = j;
sz = k;
}
//终点坐标录入
if(map[i][j][k] == 'E')
{
ex = i;
ey = j;
ez = k;
}
}
}
}
if(bfs() == 0)cout<<"Trapped!"<<endl;//无解输出被困
else cout<<"Escaped in "<<bfs()<<" minute(s)."<<endl;//有解输出用时
}
}经典问题:移动骑士
题目描述
给定一个 n∗n 的棋盘,以及一个开始位置和终点位置。棋盘的横纵坐标范围都是 [0,n),将一个国际象棋中的骑士放置在开始位置上,请问将它移动至终点位置至少需要走多少步。一个骑士在棋盘上可行的移动方式如下图所示:

输入
第一行包含整数 T,表示共有 T 组测试数据。每组测试数据第一行包含整数 n,表示棋盘大小。第二行包含两个整数 x,y 用来表示骑士的开始位置坐标 (x,y)。第三行包含两个整数 x,y 用来表示骑士的终点位置坐标 (x,y)。
输出
每组数据输出一个整数,表示骑士所需移动的最少步数,每个结果占一行。
数据范围
4≤n≤300
0≤x,y<n
输入样例
3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1输出样例
5
28
0源代码
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 300+10;
bool vis[N][N];
int ans[N][N];
//6个方向的偏移量数组
int dx[8] = {-1, -2, -2, -1, 1, 2, 2, 1};
int dy[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
//二维点结构体
struct Point
{
int x;
int y;
};
//起点终点坐标
int n,t,sx,sy,ex,ey;
int bfs()
{
queue<Point> A;
A.push({sx,sy});
vis[sx][sy] = 1;
while(!A.empty())
{
auto t = A.front();
A.pop();
for(int i = 0;i < 8;i ++ )
{
int X = t.x + dx[i];
int Y = t.y + dy[i];
if(X >= 0 && X < n && Y >= 0 && Y < n && !vis[X][Y])
{
vis[X][Y] = 1;
ans[X][Y] = ans[t.x][t.y] + 1;
if(X == ex && Y == ey)return ans[X][Y];
A.push({X,Y});
}
}
}
return ans[ex][ey];
}
int main()
{
cin >> t;
while(t -- )
{
cin >> n;
memset(vis,0,sizeof(vis));
memset(ans,0,sizeof(ans));
cin >> sx >> sy;
cin >> ex >> ey;
cout << bfs() << endl;
}
}例题精讲
首先我们先要了解国际棋盘的模样

可以发现每一个皇后的同一行、同一列、同一对角线位置均没有皇后
国际象棋皇后的走势规则即为可攻击同一行、同一列、同一对角线的其中
因此对于标记数组的定义我们可以定义行(row)、列(line)、正对角线(dg)、反对角线(udg)
row与line数组很好处理,但是对于正对角线和反对角线的处理则需要利用数学知识(一次函数)
已知一次函数的一般式为y = kx + b
对于正对角线的k为正,截距b = y - x
对于反对角线的k为负,截距b = x + y

但是要是对于题目的话,逐格遍历的做法是从左下角遍历到右下角
因此正对角线(玫红色)换作了x = - y + b 截距b = x + y
反对角线(黄色)换作了x = y + b 截距b = x - y
注意对于逐格搜索的方式y >= x 因此要保证截距为正,加上偏移量n就ok
求取截距b的原因就在于有了截距b之后则可以推出那条线,因此可以对此一次函数标记
综上所述正对角线和反对角线的标记数组由此得来
经典问题:n皇后
题目描述
给出一个 n×n的国际象棋棋盘,你需要在棋盘中摆放n个皇后,使得任意两个皇后之间不能互相攻击。具体来说,不能存在两个皇后位于同一行、同一列,或者同一对角线。请问共有多少种摆放方式满足条件。

输入
一个整数n,表示棋盘的大小。
输出
输出一行一个整数,表示总共有多少种摆放皇后的方案,使得它们两两不能互相攻击。
数据范围
1≤n≤12
输入样例
4输出样例
2源代码
#include <iostream>
using namespace std;
const int N = 1000+10;
char map[N][N];//图
bool row[N],line[N],dg[N],udg[N];//依次为行、列、正对角线、反对角线
int n,ans = 0;
void dfs(int x,int y,int num)//从上至下、从左至右逐个遍历
{
//当y发生越界的情况时,证明要往下一行搜
if(y == n)
{
y = 0;
x ++ ;
}
//当x发生越界的情况时,证明全部方格已搜索完毕
if(x == n)
{
//当皇后的个数符合要求的时候,答案加一
if(num == n)
{
ans ++ ;
}
//当皇后个数不符合要求却搜索完毕的时候则回溯
return;
}
//当下标为x y的元素在图中的同一正对角线、同一反对角线、同一行、同一列皆没有被标记的时候可以走
if(!dg[x + y] && !udg[x - y + n] && !row[x] && !line[y])
{
dg[x + y] = udg[x - y + n] = row[x] = line[y] = true;//打标记
dfs(x,y + 1,num + 1);//继续往下一个搜
dg[x + y] = udg[x - y + n] = row[x] = line[y] = false;//回溯恢复
}
//当没有符合放置皇后的情况时,继续向下一个格子搜,皇后数不变
dfs(x,y + 1,num);
}
int main()
{
cin >> n;
//注意,图的横坐标下标为0~n-1,纵坐标下标为0~n-1
dfs(0,0,0);
//dfs函数的参数依次为横坐标,纵坐标,放置皇后数
cout << ans;
return 0;
}经典问题:n皇后PLUS
题目描述
皇后plus问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。现在给定整数 n,请你输出所有的满足条件的棋子摆法。

输入
共一行,包含整数 n。
输出
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:输出顺序要按照样例的规律
数据范围
1≤n≤9
输入样例
4输出样例
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..源代码
#include <iostream>
using namespace std;
const int N = 1000+10;
char map[N][N];//图
bool row[N],line[N],dg[N],udg[N];//依次为行、列、正对角线、反对角线
int n;
void dfs(int x,int y,int num)//从上至下、从左至右逐个遍历
{
//当y发生越界的情况时,证明要往下一行搜
if(y == n)
{
y = 0;
x ++ ;
}
//当x发生越界的情况时,证明全部方格已搜索完毕
if(x == n)
{
//当皇后的个数符合要求的时候,答案加一
if(num == n)
{
for(int i = 0;i < n;i ++ )puts(map[i]);
cout<<endl;
}
//当皇后个数不符合要求却搜索完毕的时候则回溯
return;
}
//当下标为x y的元素在图中的同一正对角线、同一反对角线、同一行、同一列皆没有被标记的时候可以走
if(!dg[x + y] && !udg[x - y + n] && !row[x] && !line[y])
{
map[x][y] = 'Q';//标记为皇后的位置
dg[x + y] = udg[x - y + n] = row[x] = line[y] = true;//打标记
dfs(x,y + 1,num + 1);//继续往下一个搜
map[x][y] = '.';//回溯恢复为初始位置
dg[x + y] = udg[x - y + n] = row[x] = line[y] = false;//回溯恢复
}
//当没有符合放置皇后的情况时,继续向下一个格子搜,皇后数不变
dfs(x,y + 1,num);
}
int main()
{
cin >> n;
for(int i = 0;i < n;i ++ )
{
for(int j = 0;j < n;j ++ )
{
map[i][j] = '.';
}
}
//注意,图的横坐标下标为0~n-1,纵坐标下标为0~n-1
dfs(0,0,0);
//dfs函数的参数依次为横坐标,纵坐标,放置皇后数
return 0;
}课后习题
棋盘挑战
题目描述
给定一个 N×N 的棋盘,请你在上面放置 N 个棋子,要求满足:
- 每行每列都恰好有一个棋子
- 每条对角线上都最多只能有一个棋子
1 2 3 4 5 6
-------------------------
1 | | O | | | | |
-------------------------
2 | | | | O | | |
-------------------------
3 | | | | | | O |
-------------------------
4 | O | | | | | |
-------------------------
5 | | | O | | | |
-------------------------
6 | | | | | O | |
-------------------------
上图给出了当 N=6 时的一种解决方案,该方案可用序列 2 4 6 1 3 5 来描述,该序列按顺序给出了从第一行到第六行,每一行摆放的棋子所在的列的位置。
请你编写一个程序,给定一个 N×N 的棋盘以及 N 个棋子,请你找出所有满足上述条件的棋子放置方案。
输入格式
共一行,一个整数 N。
输出格式
共四行,前三行每行输出一个整数序列,用来描述一种可行放置方案,序列中的第 i 个数表示第 i 行的棋子应该摆放的列的位置。
这三行描述的方案应该是整数序列字典序排在第一、第二、第三的方案。
第四行输出一个整数,表示可行放置方案的总数。
数据范围
6≤N≤13
输入样例:
6
输出样例:
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
源代码
#include <iostream>
using namespace std;
const int N = 1010;
bool dg[N],udg[N],line[N];
char map[N][N];
int n,ans = 0;
void dfs(int u)
{
if(u == n)
{
ans ++ ;
if(ans <= 3)
{
for(int i = 0;i < n;i ++ )
{
for(int j = 0;j < n;j ++ )
{
if(map[i][j] == 'Q')cout << j + 1 << ' ';
}
}
cout<<endl;
}
return;
}
for(int i = 0;i < n;i ++ )
{
if(!dg[u + i] && !udg[u - i + n] && !line[i])
{
map[u][i] = 'Q';
dg[u + i] = udg[u - i + n] = line[i] = true;
dfs(u + 1);
map[u][i] = '.';
dg[u + i] = udg[u - i + n] = line[i] = false;
}
}
}
int main()
{
cin >> n;
for(int i = 0;i < n;i ++ )
{
for(int j = 0;j < n;j ++ )
{
map[i][j] = '.';
}
}
dfs(0);
cout << ans;
return 0;
}红与黑
题目描述
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。
你站在其中一块黑色的瓷砖上,只能向相邻(上下左右四个方向)的黑色瓷砖移动。
请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
输入格式
输入包括多个数据集合。
每个数据集合的第一行是两个整数 W 和 H,分别表示 x 方向和 y 方向瓷砖的数量。
在接下来的 H 行中,每行包括 W 个字符。每个字符表示一块瓷砖的颜色,规则如下
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
输出格式
对每个数据集合,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
数据范围
1≤W,H≤20
输入样例:
6 9
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
输出样例:
45源代码
#include <iostream>
#include <cstring>
using namespace std;
const int N = 50;
bool vis[N][N];
char map[N][N];
int dx[4] = {-1,0,1,0};
int dy[4] = {0,-1,0,1};
int n,m,sx,sy;
int dfs(int x,int y)
{
int ans = 1;
vis[x][y] = 1;
for(int i = 0;i < 4;i ++ )
{
int X = x + dx[i];
int Y = y + dy[i];
if(X >= 1 && X <= m && Y >= 1 && Y <= n && !vis[X][Y] && map[X][Y] == '.')
{
ans = ans + dfs(X,Y);
}
}
return ans;
}
int main()
{
while(cin >> n >> m)
{
if(n == 0 && m == 0)break;
memset(vis,0,sizeof(vis));
memset(map,0,sizeof(map));
for(int i = 1;i <= m;i ++ )
{
for(int j = 1;j <= n;j ++ )
{
cin >> map[i][j];
if(map[i][j] == '@')
{
sx = i;
sy = j;
}
}
}
cout << dfs(sx,sy) << endl;
}
return 0;
}