UP目录
一、理论基础
NSGA-II适合应用于复杂的、多目标优化问题。是K-Deb教授于2002在论文:A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-II,中提出。在论文中提出的NSGA-II解决了NSGA的主要缺陷,实现快速、准确的搜索性能。NSGA的非支配排序的时间复杂度为O(MN3)O(MN3),在种群规模N较大时排序的速度会很慢。NSGA-II使用带精英策略的快速非支配排序,时间复杂度为O(M(2N)2)O(M(2N)2),排序速度有大幅的提升。而且使用了精英策略,保证了找到的最优解不会被抛弃,提高了搜索性能。另一方面NSGA使用共享函数来使解分布均匀,该函数依赖于共享参数σshareσshare的选择,而且共享函数的复杂度高达O(N2)O(N2)。NSGA-II从新定义了拥挤距离来代替共享参数。其算法流程如下:
步骤一:
快速非支配排序。在选择运算之前,根据个体的非劣解水平对种群分级。具体方法为:将当前种群中所有非劣解个体划分为同一等级,令其等级为l;然后将这些个体从种群中移出,在剩余个体中找出新的非劣解,再令其等级为2;重复上述过程,直至种群中所有个体都被设定相应的等级。该算法有两部分组成,第一部分用于计算ni和Si。其中ni表示支配个体i的个体总数,Si表示个体i所支配的个体集合。第二部分用于求P1,P2,P3,....。Pi表示第i个前沿集合。
fast-nondominated-sort(Pop)
{ for each p ∈ Pop
{ for each q ∈ Pop then
if ( p dominated q ) then // p 支配 q
Sp = Sp ∪ {q}
else if ( q dominated p ) then // q 支配 p
np = np + 1
}end for q
if ( np == 0 ) then P1 = P1 ∪ {p}
i = 1;
while(Pi != Ø )
{ H = Ø
for each p ∈ Pi
{ for each q ∈ Sp
nq = nq -1 ;
if (nq == 0) then H = H U{q}
}end for p
i = i + 1;
Pi = H;
}end for while
}end for fast-nondominated-sort
步骤二:
编码,和单独的遗传相同,具体见上面我的介绍。
步骤三:
选择操作,经过排序和拥挤距离计算,群体中的每个个体i都得到2个属性:非支配序irank。和拥挤距离。id当irank<jrank或irank=jrank且id>jd时,i个体优于j个体。上式的意义为:如果2个个体的非支配排序不同,取序号低的个体(分级排序时,先被分离出来的个体);如果2个个体在同一级,取周围较不拥挤的个体。
一旦种群中的个体按照非支配性原则和聚集距离进行排序。个体的选择操作就可以进行。然后选择的操作的单目标遗传算法的选择过程进行。
步骤四:
精英策略。精英策略即保留父代中的优良个体直接进入子代。采用的方法是:
①将父代Pt和子代Qt全部个成为一个种群
②将种群Rt快速非支配排序并计算每一个体局部拥挤距离,依据等级的高低逐一选取个体,直到个体数量达到N就形成了新的父代种群Pt+1;
③在基础上开始新一轮的选择、交叉和变异,形成新的子代种群Qt+1。
步骤五:
和前面的介绍一样,定义交叉概率和变异概率。
步骤六:
进行交叉和变异,其杂交方式如下:
C1,k = 0.5*[ (1-βk)*P1,k + (1+βk)*P2,k)
C2,k = 0.5*[ (1+βk)*P1,k + (1-βk)*P2,k)
其中,Ci,k,表示第i个孩子第k维的值,Pi,k 表示第i个父个体第k维的值。βk是 满足一定概率密度分布的随机数。具体产生方式如下:
βk = (2*u)1/(θ+1) u < 0.5
βk = 1 / [2*(1-u)]1/(θ+1) u ≥ 0.5
其中u是(0,1)直接的随机数,θ是个常量参数。
变异方式采用多项式变异。变异计算方式如下:
![]()
其中的Ck是孩子个体,Pk是父个体,Pku 和Pkl,是第k维决策变量的定义域的上下限。δk是随机变量,满足多项式分布,其分布函数如下
δk = (2rk)1/(η+1) - 1 rk < 0.5
δk = 1 -[2(1-rk)]1/(η+1) rk >= 0.5
公式中rk是满足(0,1)均匀分布的随机数,η 是变异分布参数。
后代种群和当代种群混合,从中选择优秀的个体作为下一代种群。由于之前优秀的个体被加入混合种群中,因此,精英种群得到保护和继承。混合种群之后居于非支配性原则进行排序。下一代个体产生通过选择每个前沿集合中的个体,直到下一代种群的大小达到原来当代种群的大小。如果添加当前前沿集合Pi中的个体超过种群大小N,则从Pi中选择聚集距离大的个体。并不断重复上述的迭代操作,直到到终止条件。
二、核心程序
..................................................................
nvar=3; % number of variable
lb=[-4 -4 -4]; % lower bound
ub=[4 4 4]; % upper bound
npop=40; % number of population
pc=0.7; % percent of crossover
ncross=2*round(npop*pc/2); % number of crossover offspring
pm=0.3; % percent of mutation
nmut=round(npop*pm); % number of mutation offspring
maxiter=150;
%% initialization
empty.pos=[];
empty.cost=[];
empty.dcount=[]; % dominate count
empty.dset=[]; % dominate set
empty.rank=[];
empty.cdis=[]; % crowding distance
pop=repmat(empty,npop,1);
for i=1:npop
pop(i).pos=lb+rand(1,nvar).*(ub-lb);
pop(i).cost=fitness(pop(i).pos);
end
[pop F]=non_dominated_sorting(pop);
pop=calculated_crowding_distance(pop,F);
pop=sorting(pop);
%% main loop
for iter=1:maxiter
% crossover
crosspop=repmat(empty,ncross,1);
crosspop=crossover(crosspop,pop,ncross,F,nvar);
% mutation
mutpop=repmat(empty,nmut,1);
mutpop=mutation(mutpop,pop,nmut,lb,ub,nvar);
[pop]=[pop;crosspop;mutpop];
[pop F]=non_dominated_sorting(pop);
pop=calculated_crowding_distance(pop,F);
pop=sorting(pop);
pop=pop(1:npop);
[pop F]=non_dominated_sorting(pop);
pop=calculated_crowding_distance(pop,F);
pop=sorting(pop);
C=[pop.cost]';
figure(1)
plotpareto(F,C)
disp([ ' iter = ' num2str(iter) ' BEST F1 = ' num2str(min(C(:,1))) ' BEST F2 = ' num2str(min(C(:,2))) ' NF1 = ' num2str(length(F{1})) ])
%% results
pareto=pop(F{1},:);
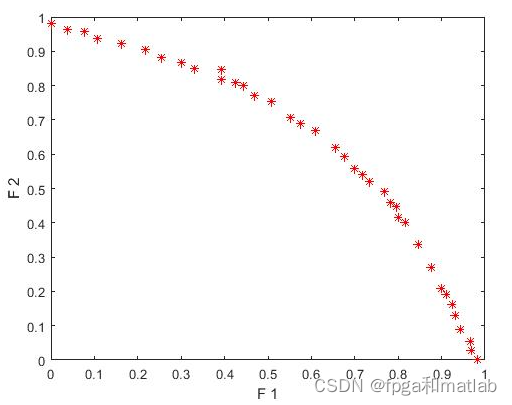
up70三、测试结果
通过matlab2021a仿真结果如下: