四、二维傅里叶变换

在此之前，文章都是对 FT 的理论部分的科普推导，距离我们的实际应用还有一定距离

虽然之前提到函数时域时，都是默认我们以时间 t 作为自变量，但事实上自变量也可以是其它含义，例如距离 x，同时可以扩展到更多维，进而，任意一张图像也可以被当作一个离散的二维函数 f(x, y)，自变量 (x, y) 可以理解为平面位置，而其值 f(x, y) 则为图像上对应坐标的通道强度或者灰度值

图像函数往往没有精确的表达式，但是依旧可以进行滤波，对于很多出名的图像处理方式：例如模糊、边缘锐化、扭曲、部分特殊风格化操作等等本质上也都是对图像“信号”的处理

再回到前面提到过好多次的教程： Games101 中的第六章：光栅化（深度测试与抗锯齿）里面就有原图像（时域）转频域的例子：

如果对 FT 没有概念，估计会对右图的具体来源比较蒙，只知道后面对频域图部分内容进行“擦除”就可以起到模糊原图的效果，不过我们能知道的信息就是，右图是通过原图傅里叶变换而来：

对于一维傅里叶变换： $F(w)=\int_{-\infty}^{+\infty} f(x) e^{-i 2\pi f x} d x$ 扩展成二维的形式就为

$F(u, v)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) e^{-i 2 \pi(u x+v y)} d x d y$

而计算机一般处理的是数字信号，只能进行有限次离散计算，因此在这种受限下的真正计算的是二维离散傅里叶变换：

$F(u, v)=\sum_{x=0}^{M-1}\sum_{x=0}^{N-1} f(x, y) e^{-i 2 \pi\left(\frac{u x}{M}+\frac{v y}{N}\right)}$ ， $u=0,1,2, \cdots , M-1 \quad v=0,1,2, \cdots , N-1$

将原图代入到 $f(x, y)$ ，经上述 DFT 后得到的频域图像 $F(u, v)$ 即右图

不过到这里应该还是不太直观，毕竟我们看到的是黑白图像，而非频域函数本身

4.1 平面正弦波与二维频率域(K-Space)

对于一维的情况：任何函数 $f(x)$ 都可以分解为无数个不同频率、不同幅值的正、余弦信号的叠加，这个性质一样可以扩展到二维：即任意一个二维图像都可以分解为无数个复平面波 $e^{-i 2 \pi(u x+v y)}$ 的叠加

而对于每一个基平面波，我们可以用一个向量 (u, v) 表示它，其单位向量对应着波的方向，而其大小 $\sqrt{x^2 + y^2}$ ，则对应着频率（这里引用一张书中的图）

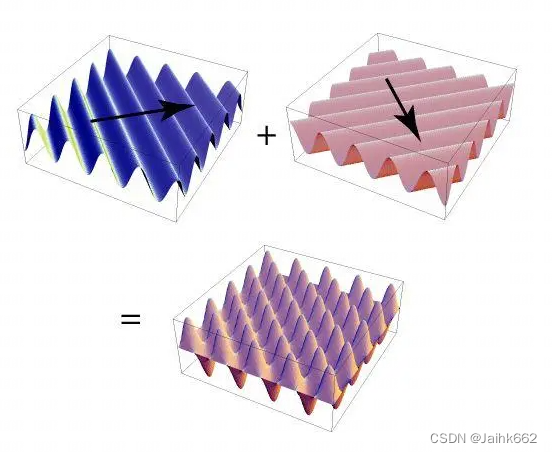
到这里，波的频率和方向有了，还差的是幅值和相位，这两者正是存在结果 $F(u, v)$ 当中的，不过还是一样，我们暂时忽略相位，只考虑幅值，可以得到一个由任意 u, v 得到的 $F(u, v)$ 的二维矩阵，如果进一步用灰度值表示幅值，那么该二维矩阵就可以表现成另一张图像，这张图像正是频域图（对应前面 PPT 的右边那张），而这个矩阵就即被称为二维频率域(K-Space)

4.2 低通滤波的含义

顾名思义，低通滤波即只允许低频率的波段通过（去掉高频信息），反之同理

这节主要思考的问题就是：为什么说我们把对应的频域图像远离中心的位置给擦除掉（低通滤波），还原后的时域图像就是原图的模糊版本呢？（相反，擦除中心区域则可以实现一个类似提取图像内容边界的效果）

首先，越是远离中心的向量 (u, v) ，其投影长度 $\sqrt{x^2 + y^2}$ 就越长，而这正对应着高频信息，其次，如果图像在有限的范围内，灰度的变化率越高，那么对应的高频信息量就越多（分解出来的波段频率越高，这个很好理解，想想一维的情况），要知道，图像越模糊，相邻的颜色变化就越平滑，这正是将图像中的高频信息从中过滤掉带来的必然结果

参考以下几个经典图像的时域和频域图，往往能更好理解前面提到的内容：

4.3 卷积核(kernel)与滤波算子

滤波可以理解为去掉一个/一段特定频率的信息，同理，滤波也同等于卷积

如果你对渲染有一定了解，那么就应该清楚实际游戏开发中，我们想要模糊一张纹理（去掉高频信息）具体是怎么做的，很明显我们并不会无脑的上 FFT，相反的，我们使用了一种非常简单的方法，那就是对每个像素及其周围的像素做平均，往往考虑性能，我们只需要做一个 3x3 的平均就能达到一个不错的模糊效果

用公式说就是：对于原图像中要模糊的区域的每一个 $f(x, y)$ ，我们都进行如下的计算：

$f'(x, y)= \frac{1}{9}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \cdot \left[\begin{array}{lll} f(x-1, y-1) & f(x, y-1) & f(x+1, y-1) \\ f(x-1, y) & f(x, y) & f(x+1, y) \\ f(x-1, y+1) & f(x, y+1) & f(x+1, y+1) \end{array}\right]$

最后得到一个新的图像，即是模糊后的效果，这个过程就叫做二维图像上的卷积，而

$\frac{1}{9}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right]$ 这种矩阵形式即叫做卷积核(kernel)，不同类别的卷积核对应不同的滤波过程，最终的效果也不尽相同：大部分的滤镜效果都是以这个为基础实现的

PhotoShop 支持我们自定义滤镜，其实就是自定义 kernel 矩阵

像泛光这种稍微高级一点的滤镜效果，往往卷积核(kernel)都会相对复杂，高斯模糊作为一个经典案例，本质就是对二维的正态分布图像做卷积，此时卷积核和大小必然不止 3x3，当然在保证效果的同时为了保证实时渲染的性能，往往都会使用额外的优化手段和算法

但是为什么这样做卷积操作，就相当于滤波了呢？可能你无法直接将两者联系到一起：

考虑到对卷积核(kernel)进行拓展，例如我们要对一张 256x256 的图做一次上面的简单模糊操作，那么我们可以对卷积核(kernel) $\frac{1}{9}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right]$ 矩阵以外的部分全部做补0的操作，补到矩阵的大小和原图像 256x256 一致，此时卷积矩阵本身就可以用另一张时域图像表示了，它的图像是下面这个样子的：中间的白色方块可想而知，正是前面矩阵中心为1的那一部分

因此，前面的操作本质上就是对两张图像进行卷积，Games101 中也有这一部分的讲解：

这张 PPT 也正好印证了前面一章提到过的卷积性质：时域的卷积可以转换为频域的乘积，反之亦然，这个性质在对图像的 FT 上必然也是成立的

好了，这下卷积和滤波就成功对应上了，显而易见：时域卷积 = 频域图像相乘 = 对前频域图像的过滤，取交集，从而做到前面说的“抠掉”频域中的高频部分，以实现滤波的作用

4.4 纹理采样与抗锯齿

兜兜转转终于回到了 Games101 中的第六章：光栅化（深度测试与抗锯齿）中的主题，可以说这几篇文章也就是对这个视频的完备讲解，也因为视频已经讲得很好，这里就没必要再细致讲解，只以简单的例子作为概括

无论是锯齿，还是摩尔纹，都是由于对连续图像进行离散采样时，采样点数量不足或间隔过大所导致的，直接原因是图像高频信息的丢失/混叠：

举个非常简单的例子：00112233445566 这一串数字，如果我每隔两个数字采样一次，那么得到的结果就是 0123456，这两者表现出来的形式是非常相似的，因而可以说这是一次成功的采样/数据压缩，但是同样的采样手段，对于数字串 01020305030201，却会采样出完全错误的结果：0000000，从而出现信息丢失无法恢复的情况

函数图像的采样也一模一样：

蓝色为实际的图像，而黑色是采样后线性过滤后，真正展现给我们看的图像，可以看到其出现了严重的失真（摩尔纹的产生原理），换句话说：越是高频的信息，我们越需要更高频的进行采样

好了，讲完了其实内容就这么简单

课件里还提到过一个问题：为什么我们的抗锯齿要先模糊再采样，而非先采样再模糊？

Answer：没对图像做滤波就先采样，丢失的高频信息就再也回不来了，后面的模糊就必然失去了它的本质意义，亡羊补牢，为时已晚

4.4.1 频域混叠现象

上面的内容同样可以利用前面章节的知识，用数学的语言描述，现在让我们穿越回前面的第二章第一节，关于采样的那一部分讲解

这张图又双叒叕来了：

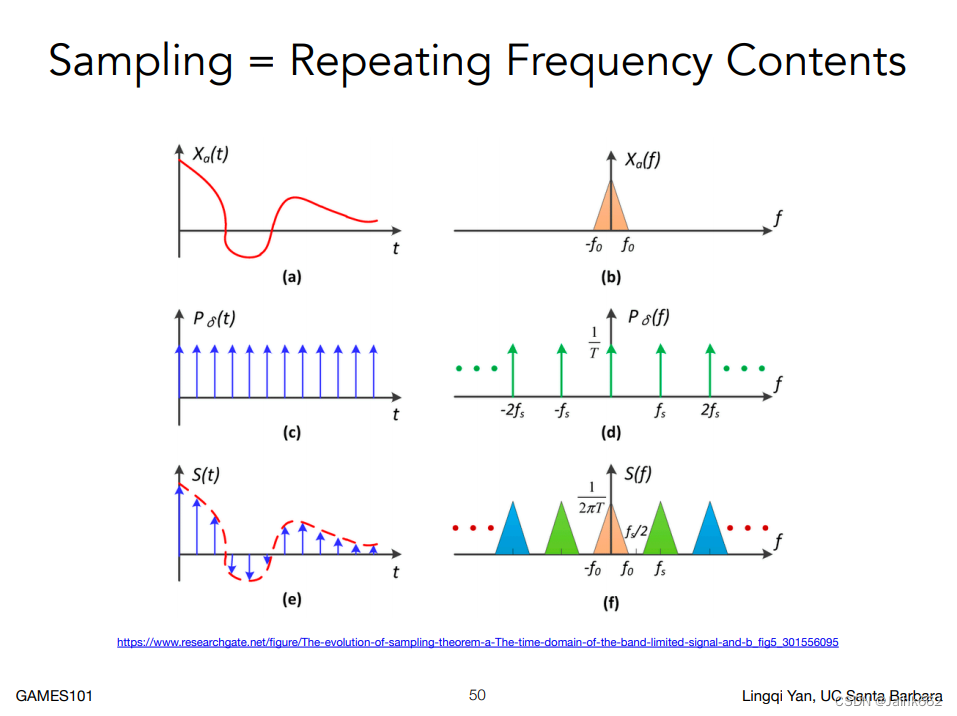
从左侧的时域图就可以看出：①采样就是原函数对一段连续冲激函数做乘积，然后还就是那个重复了很多遍性质：②时域的卷积可以转换为频域的乘积，反之亦然，最后，我们在第一章最后面埋下了一个伏笔：③形象解释了为什么冲激函数序列（梳状函数）的频域图像仍然是个冲激函数序列，好了三者一结合，我们就可以得到一个神仙结论（PPT 右侧）：采样就是在重复原始信号的频谱，以及它经过计算得到的推论：采样的间隔越大，频谱上原信号的周期延拓间隔就越小，反之亦然

到这，就又引出了一个新的概念：混叠

可想而知，只要原频谱图像不是一个冲激函数图像，那么随着卷积后频谱上原信号的周期延拓间隔变小，它们必然会在某一个时刻出现重叠（此时采样频率必然小于2倍的信号频率），这就叫做混叠，只要出现了混叠现象，那么我们就无法从频谱图像还原出准确的时域图像

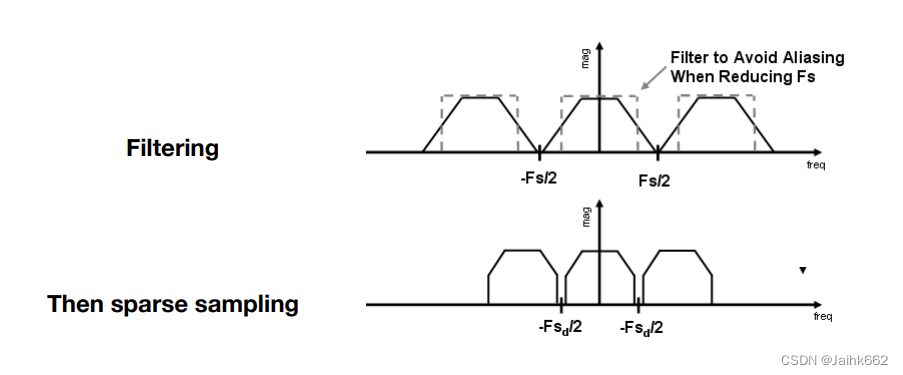
因此，反正高频信息无法正常恢复，不如我们在采样之前直接滤掉高频信息，也就是对图像做模糊处理，再采样，这也是抗锯齿的主要思路

4.4.2 奈奎斯特频率(Nyquist frequency)

当然这里还会有个问题可能还没有解释清楚，发生混叠和滤波，看上去最终的结果都是高频信息的丢失，那为什么提前滤波就可以，而坐视不管最后信号混叠就不行？

一句话解释：信号混叠不仅仅是高频信号丢失的问题，而是高频信号错误的展现成了低频信号的形式，这就如同病变的细胞一般，一定要去除而不能任由其发展

还是这张图，可以看到：只要采样频率低于2倍的信号频率，那么原本的高频信号被采样成低频信号，其实这种现象在我们生活中也经常见到，例如当马车越走越快时，马车车轮似乎越走越慢，甚至会朝反方向运转，又或者是小时候教室里的吊扇，当转速越来越快时，出现的现象是先顺时针旋转，然后静止，然后逆时针旋转，是的，人眼其实也有一定的采样频率

奈奎斯特频率(Nyquist frequency)就是为防止信号混叠需要定义最小采样频率，一般而言，该频率为信号频率的2倍，不过在计算机渲染领域，无脑的增大采样密度（超采样、游戏设置支持的前提下换更高分辨率的电子屏幕）在大部分情况下都是不太现实的事情，因此我们往往采用其他的手段去解决问题

所以关于采样这里就不再进一步了解了，有兴趣的朋友可以直接学习《信号与系统》以及《数字图像处理》，这里只是提一下作为科普

4.5 附录1：滤波技术在 ShadowMapping 软阴影中的应用

常规操作，再讲一个应用，在此之前就已经发过一篇关于 ESM 阴影的文章：UnityShader17.1：ESM 阴影技术里面也已经提到过了滤波的概念及作用，当然这里我们可以对这一部分内容做进一步的介绍和解释

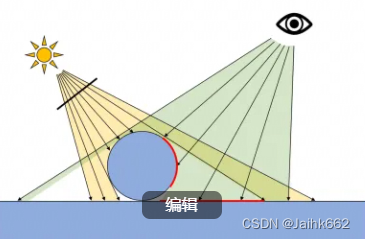
了实现软阴影，低通滤波是一个必不可少的操作，不过和前面不同的是，在计算最终阴影的过程中，我们其实有两次滤波的机会：分别是最终对最终阴影计算结果 $f(d,z)$ 进行滤波（其中 d 为光源深度，z 为 shadowmap 的采样结果）以及直接对 shadowmap（也就是 z 值）进行滤波，用数学语言描述就是：

令 $d$ 为这一点到光源的距离， $z(p)$ 为 p 点采样 shadowmap 的结果，那么 $f(d,z(p))$ 则为最终光贡献（1为完全受光，0则完全在阴影之中）

而为了实现平滑，我们可以有两种卷积滤波方式：

对结果滤波 $f'(d,z) = [w * f(d(x), z)](p)$ ，（PCF 主要思路）
对 shadowmap 预滤波： $f'(d,z) = f(d(x),(w * z)(p))$ （ESM 主要思路）

从性能上考量：方案①避免不了在片段着色时对 shadowmap 的多次采样，要知道采样开销其实并不小，这还没考虑算法的复杂度，因此方案②往往是一个更佳的选择，更何况对于静态物体投射的阴影，我们还可以对 shadowmap 进行离线处理

但是，往往事情没有这么简单，因为并不是什么情况下都可以预滤波(pre-filtering)，这取决于 $f(d, z)$ 的图像，对于最基本的形式

$f(d, z) =\left\{\begin{array}{l} 1, d<z \\ 0, d \geq z \end{array}\right.$

必然不满足 $f(d(x),(w * z)(p))=[w * f(d(x), z)](p)$ ，并且由于阶跃函数得到的一定是非0即1的结果，因此对于 z 无论如滤波都起不到正确模糊的效果

那么哪种情况可以对 z 进行滤波呢？

ESM 就是一个经典的例子： $f(d, z)=e^{-c d} e^{c z}$ ，其将阶跃函数换成了指数乘法，并且对于 d > z 的情况，还保证了图像结构不会有太大变化，此时

$\begin{aligned} s_f(x)=w * f(d(x), z) =w * (e^{-c d(x)} e^{c z}) =e^{-c d(x)} w * e^{c z} \end{aligned}$ 满足上式

除此之外还有卷积阴影(Convolution Shadow Maps)等其它算法，本质上都是对 $f(d, z)$ 做文章，例如将 $f(d, z)$ 直接傅里叶展开后取前 k 项以实现对前阶跃函数的拟合，不过无论是哪一种，基本上都能通过预滤波来实现最终的阴影柔和

FT 在图像处理中的应用