群
代数体系：集合+运算
运算及关系
- 集合与映射
1、定义：设\(A_0\)为A的子集，定义\(A_0\)到A的映射
i：\(A_0\)->A
使得i(x)=x，x∈\(A_0\)，称i为\(A_0\)到A的嵌入映射。
2、定义： 设\(A_0\)为A的子集，f为A到B的映射，g为\(A_0\)到B的映射，如果f(x)=g(x)，
∀x ∈\(A_0\) ，称f是g的开拓，g为f(在\(A_0\)上)的限制。记为
\(g=f|_{A_0}\)
- 交换图
有3个映射
- \(f_1:A_1->A_2\)
- \(f_2:A_2->A_3\)
- \(f_3:A_3->C\)
将这3个映射复合，有
\(f_3f_2f_1:A_1->C\)
另外2个映射
- \(g_1:A_1->B\)
- \(g_2:B->C\)
将这2个映射复合，也有
\(g_2g_1:A_1->C\)
则有
\(f_3f_2f_1=g_2g_1\)
则有交换图
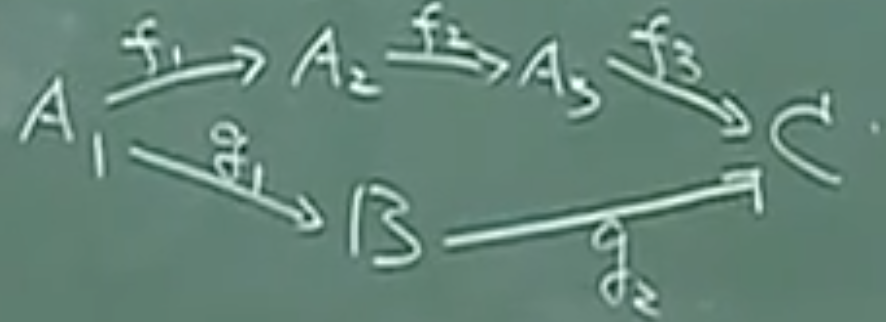
该交换图与\(f_3f_2f_1=g_2g_1\)就是一回事。
嵌入映射的交换图为
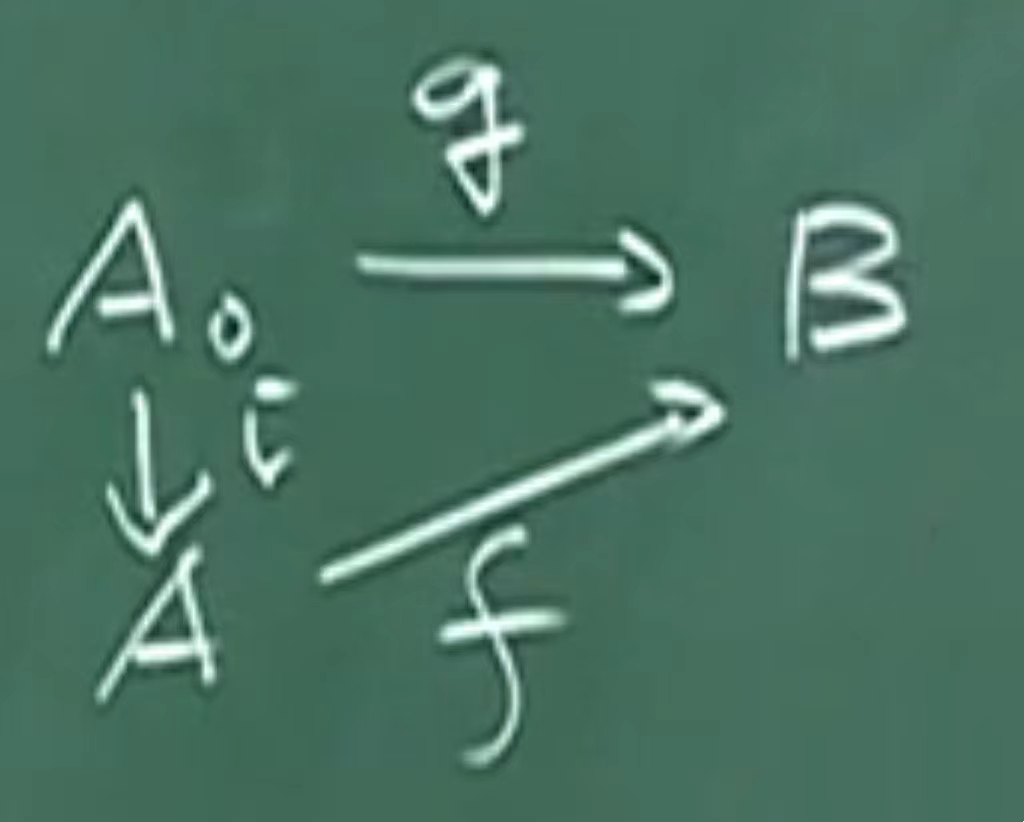
3、定义：设\(A_1,A_2\)为两个非空集合，令
\(A_1×A_2=\{(a,b)|a∈A_1,b∈A_2\}\)
集合\(A_1×A_2\)称为\(A_1\)与\(A_2\)的直积。
- 运算
加、减、乘、除
本质：两个元素——>一个元素 (其中——>为运算法则)
4、定义：设A,B,D为三个非空集合，一个映射
f：A×B->D
称为A与B到D的一个代数运算。
如果A,B,D都相同，代数运算f称为A上的二元运算。
示例1：设V是一个线性空间，数域为P，
V中加法： V×V->V （二元运算）
P与V的数乘： P×V->V
示例2：P为数域，\(P^{n×n}\)为P上n阶方阵的集合
矩阵加法，乘法都是\(P^{n×n}\)与\(P^{n×n}\)到\(P^{n×n}\)的代数运算。这也是一个二元运算。
我们在实数范围内的加和乘都是二元运算。
使用映射的形式是非常不方便的，如二元运算f：A×A->A，这个集合我们每次都写成f(a,b)，这里a,b都属于A，如果又来一个c∈A，那么我们又得写成f(f(a,b),c)，又来一个d∈A，又得写成f(d,f(f(a,b),c))，这样是非常麻烦的，而且它可能不满足交换律，如矩阵乘法。
对于这种情况，我们可以将f(a,b)简写为a∘b或者ab，那么f(d,f(f(a,b),c))就可以写成(d(ab)c)，如果满足结合律的话，又能写成dabc，这样的形式就会非常简单。在二元运算中将不再使用映射的形式来表述，而是使用这种简化的形式来表述。
- 运算规律
5、定义：设A(非空)上定义了二元运算，满足
ab=ba ∀a,b∈A
称二元运算满足交换律
6、定义：设A(非空)上定义了二元运算，满足
a(bc)=(ab)c ∀a,b,c∈A
称二元运算满足结合律
7、定义：设A上定义了两种二元运算∘,+，满足
a∘(b+c)=a∘b+a∘c ∀a,b,c∈A
称满足"∘"对"+"的左分配律
(b+c)∘a=b∘a+c∘a ∀a,b,c∈A
称满足"∘"对"+"的右分配律
它们统称为分配律
因为有了结合律，A中的代数运算\(a^n\),n∈N(正整数)才有意义(无视顺序的运算)，又由交换律，才有
\((ab)^n=a^nb^n\)
如果不满足交换律，上式其实是不成立的。
- 运算表
对于映射
f：A×B->D
当A,B都是有限集合的时候，即
|A|<∞,|B|<∞，运算符号为∘
这里A={\(a_1,a_2,a_3,...,a_m\)}，B={\(b_1,b_2,b_3,...,b_n\)}，则有运算表
| ∘ | \(b_1\) | \(b_2\) | ... | \(b_n\) |
|---|---|---|---|---|
| \(a_1\) | \(a_1∘b_1\) | \(a_1∘b_2\) | ... | \(a_1∘b_n\) |
| \(a_2\) | \(a_2∘b_1\) | \(a_2∘b_2\) | ... | \(a_2∘b_n\) |
| ... | ... | ... | ... | ... |
| \(a_m\) | \(a_m∘b_1\) | \(a_m∘b_2\) | ... | \(a_m∘b_n\) |
示例1：A={1,2}，B={1,2}，D={奇,偶}
定义f：A×B->D
假设有运算关系
1∘1=奇，1∘2=偶，2∘1=偶，2∘2=奇 (注意这里不是乘法关系，只是一种映射关系)
用运算表来表示，有
| ∘ | 1 | 2 |
|---|---|---|
| 1 | 奇 | 偶 |
| 2 | 偶 | 奇 |
这里A=B，它是一个二元运算，是一种交换运算
构造新集合的方法——关系
关系：集合A≠Ø中一种对两个元素而言的一种性质，使A中任何两个元素或有这种性质或没有这种性质，二者必居其一。
如A=IR(实数)，例如">","=","≥"这一类关系
a,b∈IR，则我们就可以判断是否a>b，a=b，a≥b，这些就可以明确，不会出现不知道的情况
那么">","=","≥"都是A中的关系，所有有关系的元素对构成A×A的子集，用R来表示，a与b有关系R，记为aRb，则
R={(a,b)|aRb}
如果a与b无关系R，记为a
b。
反之，A×A中一个子集R，则可定义关系R使aRb <==> (a,b)∈R
即为只要存在关系就可以得到子集，只要有这样的子集就可以定义关系。
8、定义：设A≠Ø，A中的一个关系为A×A中的一个子集R。
示例1：设A=IR，考虑"≤","="，对应的子集合为
上图中阴影的部分以及
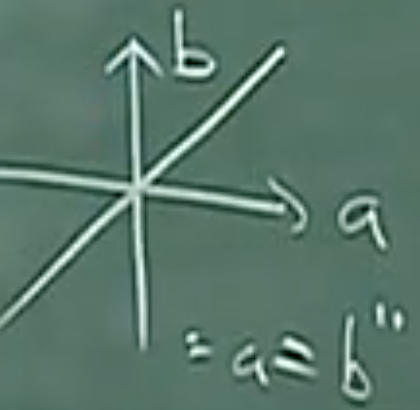
上图中的直线。
9、定义：设A≠Ø中定义了关系R，若R满足条件
- 反身性：∀a∈A，aRa (不满足所有的关系，如a>a)
- 对称性：aRb => bRa (不满足所有的关系，如a≤b)
- 传递性：aRb，bRc => aRc
则称R为等价关系。
示例2："≤"不是IR中的等价关系，不满足第二条。\(IP^{n×n}\)(矩阵)中"相似"关系为等价关系，\(A=T^{-1}BT\)，(有关矩阵相似的内容可以参考线性代数整理(三) 中的矩阵相似型)
10、定义：设A≠Ø，A的一个划分是指A中一些子集合的集合，满足∀a∈A，a包含且只包含在一个子集合中。
其意义就是A中的一个划分就是将A写成一些不相交的非空子集合的并。
\(A=∪_{i∈I}A_i\),\(∀i,A_i≠Ø\)
\(∀i,j∈I,i≠j,A_i∩A_j=Ø\)
{\(A_i\)}就是新的集合
定理一：A的一个分类决定A中一个等价关系。
证明：设\(A=∪_{i∈I}A_i\),\(A_i≠Ø\),\(i≠j,A_i∩A_j=Ø\)
定义关系R：aRb <=> ∃i使a,b∈\(A_i\) (a与b在同一个类中)
- 反身性：aRa,a跟a肯定是同一个类
- 对称性：aRb => bRa，a和b是同一个类，b和a肯定也是同一个类
- 传递性：aRb，bRc => aRc， ∃i使a,b∈\(A_i\) ,∃j使b,c∈\(A_j\)，\(A_i∩A_j≠Ø\)，故i=j，a,c ∈\(A_j\) ，故aRc
R为等价关系，得证。
该定理的反向也成立。
由等价关系可以推出一系列的新的定义：等价类、商集合、自然映射。
11、定义：设A≠Ø，A中有一个等价关系R，a∈A，定义a的等价类
={b∈A|aRb}(或称为a所在的等价类[a]，与元素a有等价关系的所有元素构成的集合)
12、定义：设A≠Ø，A中定义了等价关系R，定义集合A/R={|a∈A}(重复的只取一个)，称为A对R的商集合(所有等价类的集合)。
13、定义：映射π：A->A/R，π(a)=，称为A到A/R的自然映射。
定理二：A中一个等价关系R决定A中的一个分类。
证明：A/R就是A的一个分类，∀∈A/R，⊆A，≠Ø，\(A=∪_{a∈A}\)(重复的只取一个)
≠
，若∩≠Ø，取c∈∩
c∈，aRc
c∈，bRc
由对称性，bRc,cRa，再由传递性，得bRa
故=，矛盾，故≠，则∩=Ø，
故A/R为A的一个分类，得证
由以上的两个定理，可知
等价关系 <-> 分类
14、定义：设A≠Ø，A中定义了二元运算"∘"，又定义了等价关系R，如果R与"∘"满足条件
\(a_1Rb_1,a_2Rb_2=>a_1∘a_2Rb_1∘b_2\)
则称R是"∘"的同余关系
如果R是"∘"的同余关系，在A/R中定义
=
(其中a,b为代表元)，当然中可能有c≠a，中可能有d≠b，则可以写成
=
这里和是同一个等价类，和是同一个等价类
可能a∘b≠c∘d，同余关系可以保证=
A，"∘"，等价关系R为"∘"的同余关系
代数体系(集合加运算){A;∘} ——> 新的代数体系{A/R;}。这是我们这里最重要的内容，由原有的代数体系构建出新的代数体系。
示例2，设Z(整数集合)中取m>0，定义关系R
aRb <=> m|b-a (m整除b-a)
Z中关系R为等价关系，称为模m的同余关系，aRb记为a≡b(mod m)
Z中有+,×；R为"+","×"的同余关系
如果我们考虑模 ( n ) 的同余关系，则整数集合会被划分为 ( n ) 个等价类，每个等价类中的数对模 ( n ) 同余。例如，考虑模 ( 3 ) 的同余关系，整数集合被划分为三个等价类：
- ( [0] ) 包含所有能被 ( 3 ) 整除的整数，如 ( {..., -9, -6, -3, 0, 3, 6, 9, ...} )。
- ( [1] ) 包含所有除以 ( 3 ) 余 ( 1 ) 的整数，如 ( {..., -8, -5, -2, 1, 4, 7, 10, ...} )。
- ( [2] ) 包含所有除以 ( 3 ) 余 ( 2 ) 的整数，如 ( {..., -7, -4, -1, 2, 5, 8, 11, ...} )。
示例3，\(IP^{n×n}\)中定义关系R(n≥2)
ARB <=> |A|=|B| (行列式相等)
R为\(IP^{n×n}\)中的等价关系
R对“+”不是同余关系
R对矩阵乘法是同余关系
半群与群
群=非空集合+二元运算+性质
15、定义：设G为一个非空集合，G上有二元运算∘，满足结合律(无视运算顺序)，则称{G;∘}(或G)为一个半群。
示例1：IN(自然数集合，0∉IN)，{IN;+}为一个半群；{IN;⋅}也是一个半群。
示例2：设A≠Ø，M(A)为A中所有变换(A->A映射)的集合。{M(A);∘}为半群。
示例3：设A≠Ø，P(A)为A的幂集(即A所有子集的集合，包含空集)，则{P(A);∪}(\((A_1∪A_2)∪A_3=A_1∪(A_2∪A_3)\))为半群。
{P(A);∩}为半群。
16、定义：设{G;∘}为半群，若元素\(e_1∈G\)，满足∀a∈G，\(e_1∘a=a\)，则称\(e_1\)为G的左幺元； 满足∀a∈G，\(a∘e_2=a\)，则称\(e_2\)为G的右幺元。这里需要注意的是左幺元和右幺元不是完全等价的，有些半群只有左幺元没有右幺元；有些半群只有右幺元没有左幺元。若e∈G既是左幺元又是右幺元，则称e为G的幺元，G称为幺半群。
{IN;+}没有幺元，不是幺半群；{IN;⋅}的幺元为1，{M(A);∘}的幺元为id(恒等映射)，{P(A);∪}的幺元为Ø，{P(A);∩}的幺元为A，它们都是幺半群。
17、定义：设{G;∘}为幺半群，e为幺元，a∈G，若元素a'满足a'∘a=e，则称a'为a的左逆元；若元素a''满足a∘a''=e，则称a''为a的右逆元。若b∈G，既是a的左逆元又是a的右逆元，a∘b=b∘a=e，则称b是a的一个逆元，记为\(a^{-1}\)。交换的群称为Abel群。
示例4：任何一个数域IP对数的加法为群。Abel群。
Abel群是一种在特定运算下满足以下五个性质的代数结构：
- 封闭性：任意两个元素的和仍在该数域内。
- 结合律：对任意三个元素a、b、c，有(a+b)+c = a+(b+c)。
- 幺元存在性：存在一个元素0（我们称之为加法幺元或零元），对任意元素a，都有a+0=a。
- 逆元存在性：对任意元素a，都存在一个元素-b（我们称之为a的加法逆元），满足a+(-b)=0。
- 交换律：对任意两个元素a和b，有a+b=b+a。
示例5：数域IP对乘法不是群，只是幺半群，因为0乘以任何数为0，它是不可逆的。但对于\(IP^*=IP|\{0\}\)(去除0的数域)对乘法为Abel群。
示例6：{1,-1}对乘法成Abel群，当集合为有限的时候，可以用表来表示
| × | 1 | -1 |
|---|---|---|
| 1 | 1 | -1 |
| -1 | -1 | 1 |
在群中，该表称为群表。
示例7：设A≠Ø，S(A)为M(A)中所有可逆的变换的集合，对∘成一个群，称为A的全变换群。
命题1：幺半群的幺元唯一。
证明：设e,e'为半群G的幺元，则
e=ee'=e' 得证
命题2：设G是群，则G中任一元的逆元唯一。
证明：设a∈G，\(a_1,a_2\)均为a的逆元，e为幺元，则
\((a_1a)a_2=ea_2=a_2\)
\(a_1(aa_2)=a_1e=a_1\)
故\(a_1=a_2\) 得证
群的定义：幺半群G中每一个元素都可逆，G称为群。
集合观点：G≠Ø，定义了二元运算∘
- G对∘封闭
- ∘满足结合律
- G存在幺元e：e∘a=a∘e=a,∀a∈G
- ∀a∈G，a存在逆元：∃b使a∘b=b∘a=e
这是群的第一种定义，我们也可以弱化这个定义，修改一下第3、4条如下
3'.G中存在左幺元e：e∘a=a,∀a∈G
4'.∀a∈G，a存在左逆元：∃b使b∘a=e
那么群的第二种定义：1、2不变，3、4换成3'、4‘.
3''.G中存在右幺元e：a∘e=a,∀a∈G
4''.∀a∈G，a存在右逆元：∃b使a∘b=e
那么群的第三种定义：1、2不变，3、4换成3''、4''.
- 群的基本性质
命题3：群满足左右消去律
证明：设a,b,c∈G, ab=ac
用a的逆元\(a^{-1}\)左乘得
\(a^{-1}(ab)=a^{-1}(ac)\)，由结合律
\((a^{-1}a)b=(a^{-1}a)c\)，得
b=c
故群满足左消去律，右消去律类似，得证
命题4：设G为群，则对任何a,b∈G，方程：ax=b,xa=b都存在唯一解。
证明：对ax=b，用\(a^{-1}b\)代替x，左右相等，解存在。
若\(c_1,c_2\)都是ax=b的解，则
\(ac_1=ac_2=b\)
由消去律，有
\(c_1=c_2\)
故解唯一，xa=b类似，得证
命题5：设G为半群，若∀a,b∈G，方程：ax=b,xa=b都有解，则G为群
证明：根据1、2、3'、4'
由于G为半群，1、2成立
∀a∈G，由方程xa=a存在解\(e_a\)
∀c∈G，方程ax=c有解d，则c=ad，则
\(e_ac=e_a(ad)=(e_aa)d=ad=c\)
故\(e_a\)为左幺元
∀b∈G，方程\(xb=e_a\)有解，解为b的左逆，G为群，得证
命题6：有限半群G若满足左右消去律，则G为群
证明：|G|<∞，设G={\(a_1,a_2,a_3,...,a_n\)}
考虑方程：\(a_ix=a_j\)，元素\(a_ia_1,a_ia_2,a_ia_3,...,a_ia_n\)
若l≠k，使\(a_ia_l=a_ia_k\)，由左消去律得
\(a_l=a_k\)
矛盾
故\(a_ia_1,a_ia_2,a_ia_3,...,a_ia_n\)互不相等，必有一个为\(a_j\)
\(a_ix=a_j\)有解，类似可证\(xa_i=a_j\)有解
由命题5，G是群，得证
反例：IN(自然数集合，非有限)对乘法，不是群。
- 记号：
a∈G，\(a^n\)，n>0，若G为群，\(a^n\)，n>0，\(a^n=aa...a\)(n个a)
\(a^0=e\)，\(a^{-1}\)=a的逆，\(a^{-n}=a^{-1}a^{-1}...a^{-1}\)(n个\(a^{-1}\))
\(a^m\),m∈Z(整数)，\(a^ma^n=a^{m+n}\)，\((a^m)^n=a^{mn}\)
G为乘法群
G为交换群，一般将运算写成加法。
n>0，na=a+a+...+a(n个a)
a的逆写成-a，(-n)a=(-a)+(-a)+...+(-a)(n个-a)
0a=0(G的幺元，称为零元，记为0)
群与对称，对称即群
欧几里德空间：刚体运动成群——刚体运动群。
平面图形γ：保持γ整体不变的刚体运动成群。
V|IP GL(V)={V中可逆线性变换}也是群，这里V是线性空间，IP为数域。
- 元素的基本性质
18、定义：设G为群，G的阶指G中元素的个数，记号|G|，|G|<∞，称G为有限群；|G|=∞，称G为无限群。|G|<∞，可以用群表表示。
19、定义：设G为群，a∈G，若对任何的n∈IN(自然数)，\(a^n≠e\)，称a的阶为无穷(a元素与自身累运算后无法回到幺元)；若至少存在一个m∈IN，使\(a^m=e\)(乘法群，若为加法群则为ma=e，也就是说a元素与自身累运算后回到幺元)，定义a的阶为\(min\{k∈IN|a^k=e\}\)(能回到幺元的最小运算次数，若为加法群则为ka=e的k最小)，或记为|a|，显然
- a的阶为1<=>a=e (1阶的元素只有幺元)
- a的阶与\(a^{-1}\)的阶相等。
命题7：设G为群，a∈G，则a的阶为无穷<=>\(...,a^{-n},a^{-n+1},...,a^{-1},e,a,a^2,...,a^n,...\)序列不出现重复，即\(a^m≠a^n\)，∀m,n∈Z，m≠n。
证明：若a的阶无穷，设∃m≠n使\(a^m=a^n\)
设m>n，则\(a^{m-n}=e\)，矛盾
故∀m≠n，\(a^m≠a^n\)
反之，若∀m≠n，\(a^m≠a^n\)，则∀m∈IN，\(a^m≠a^0=e\)
故a的阶为无穷，得证
命题8：设G为群，a∈G，a的阶为d(即为\(a^d=e\))，则
- \(a^k=e<=>d|k\) (d整除k)
- \(a^k=a^h<=>d|h-k\) (每隔d的间隔重复一次)
证明：只证1，设k=dm，则
\(a^k=a^{dm}=(a^d)^m=e^m=e\)
另一方面，设\(a^k=e\)，设k=dq+r，q,r∈Z，0≤r<d
若r≠0，则\(a^r=a^{k-qd}=a^k⋅(a^d)^{-q}=e\)与a的阶为d矛盾
故r=0，即d|k，1得证
命题9：设G为群，a∈G，a的阶为d，则
- \(a^k\)的阶为d/(d,k) ((d,k)表示最大公因数，k>0)
- \(a^k\)的阶为d<=>(d,k)=1
证明：只证1，设\(a^k\)的阶为q
设\(d=d_1(d,k)\)，\(k=k_1(d,k)\) (这里\(d_1,k_1\)为因子)
则\((a^k)^q=e=a^{qk}\)，故
d|qk，即\(d_1|k_1q\)，因\((d_1,k_1)=1\) (互素)
故\(d_1|q\)
故d/(d,k)|q
反之，\((a^k)^{d_1}=a^{kd_1}=a^{k_1(d,k)d_1}=a^{k_1d}=(a^d)^{k_1}=e\)
因\(a^k\)的阶为q，故\(q|d_1=d/(d,k)\)
故\(q=d/(d,k)\)，得证
由此已知一个元素的阶，就可以知道它的幂次的阶。
命题10：设G为群，a,b∈G，a的阶为m，b的阶为n，且ab=ba，(m,n)=1，则ab的阶为mn。
证明：设ab的阶为q，因为ab=ba，有
\((ab)^{mn}=a^{mn}b^{mn}=e⋅e=e\)
故q|mn
另一方面，因为ab=ba
\(b^{qm}=a^{qm}b^{qm}=(ab)^{qm}=((ab)^q)^m=e^m=e\)
因b的阶为n，得
n|qm
又由(m,n)=1，得
n|q
又由\(a^{qn}\)可得
m|q
又(m,n)=1，mn|q，故
q=mn 得证
子群与商群
- 子群
20、定义：设G为群，H⊆G，H≠Ø，若H在G的运算构成群，则称H为G的子群，记为H<G。
示例1：两个数域\(IP_1⊆IP_2\)，则{\(IP_1;+\)}<{\(IP_2;+\)}。
{\(IR^+;⋅\)}<{\(IR^*;⋅\)} (\(IR^+\)为正实数集合，\(IR^*\)为去0的实数集合，⋅表示为乘法群)
{{1,-1};⋅}<{\(IR^*;⋅\)}
{\(IR^*;⋅\)}不是{IR;+}的子群。
示例2：设V为线性空间，dimV<∞，\(S_V\)为V的全变换群，设GL(V)为所有可逆的线性变换组成的集合，GL(V)<\(S_V\)。GL(V)称为V上的一般线性群。
记SL(V)为V中行列式为1的线性变换的集合，SL(V)<GL(V)，SL(V)称为特殊线性群。
V/IP(数域IP上的线性空间)，GL(n,IP)(n阶方阵的一般线性群)，SL(n,IP)<GL(n,IP)
示例3：mZ={mn|n∈Z},m∈IN，mZ为整数加法群，mZ<Z
- 子群的基本性质
H与G的运算一致=>G的幺元e∈H。
设H的幺元为e'，ee'=e'=e'e'，由消去律，得
e=e'
∀h∈H，h在G中的逆\(h^{-1}\)∈H，也就是h在H中的逆。
定理三：设G为群，H为G的非空子集，则下列条件等价
- H<G
- ∀a,b∈H,ab∈H,\(a^{-1}∈H\) (封闭性)
- ∀a,b∈H,\(ab^{-1}∈H\)
证明：由1->2，没问题
由2->3，因为a,b∈H，则\(a,b^{-1}∈H\)
故\(ab^{-1}∈H\)
由3->1，∀a,b∈H，\(aa^{-1}∈H\)，e∈H，b∈H=>\(b^{-1}∈H\)
\(a,b^{-1}∈H\)=>\(a(b^{-1})^{-1}=ab∈H\)
由以上的所有条件都成立可得H<G。
该定理为我们判断一个群是否是另一个群的子群提供了判断依据。
命题11：设H为群G的非空有限子集，则
H<G <=> H对运算封闭
证明：H如果为子群，则必然对运算封闭
反之，H对运算封闭，结合律成立，H为有限半群，又H为G的子集，消去律成立
故H<G
命题12：设\(H_1<G,H_2<G\)，则\(H_1∩H_2<G\)
证明：因为\(e∈H_1∩H_2\)，故\(H_1∩H_2≠Ø\)
\(∀a,b∈H_1∩H_2\)，则\(a,b∈H_1\)，\(a,b∈H_2\)
故\(ab^{-1}∈H_1\)，\(ab^{-1}∈H_2\)
故\(ab^{-1}∈H_1∩H_2\)
由定理第3条可得\(H_1∩H_2<G\)，得证
注：\(H_1∪H_2\)一般不为子群，但满足特定条件可以为子群。
21、定义：设G为群，H<G，a∈G，定义
- aH={ah|h∈H} (加法群为a+H)
- Ha={ha|h∈H} (加法群为H+a)
1、2分别称为a为代表元的H的一个左陪集和右陪集。
假设我们有一个整数模 (5) 的加法群 (G={0, 1, 2, 3, 4})，这里的群运算是模 (5) 的加法。取子群 (H = {0, 2, 4})，这个子群实际上是 (G) 中所有偶数构成的集合。现在，我们选择一个元素 (a = 1) 来构造左陪集。
左陪集 (aH) 或者 (1 + H) 就是将 (1) 加到子群 (H) 中每个元素上：
[ 1H = {1 + h |h∈H} = {1 + 0, 1 + 2, 1 + 4} = {1, 3, 0} ]
因为我们在模 (5) 的加法群中，所有的加法都是模 (5) 进行的。所以，左陪集 (1H) 包含了元素 (1, 3, 0)。
同样，如果我们选择另一个元素 (a = 3)，我们可以构建另一个左陪集：
[ 3H = {3 + h|h∈H} = {3 + 0, 3 + 2, 3 + 4} = {3, 0, 2} ]
这里我们看到了左陪集 (3H) 实际上和子群 (H) 是相同的，这是因为 (3) 是子群 (H) 的一个元素，而子群 (H) 的任何元素与其自身的左陪集总是等于 (H) 本身。
定理四：设G为群，H<G，则关系
aRb <=> \(a^{-1}b∈H\) (加法群为aRb <=> b-a∈H)
这是一个等价关系，a所在的等价类
=aH
故a的所有左陪集构成G的一个分类。
证明：R为关系，∀a∈G，\(a^{-1}a=e∈H\)
故aRa，反身性成立
若aRb，则\(a^{-1}b∈H\)
则\((a^{-1}b)^{-1}=b^{-1}a∈H\)
故bRa，故对称性成立
若aRb，bRc，则\(a^{-1}b∈H\)，\(b^{-1}c∈H\)
因H<G，\((a^{-1}b)(b^{-1}c)=a^{-1}c∈H\)
故aRc，传递性成立
故R为等价关系
证=aH，对任何h∈H
\(a^{-1}(ah)=h∈H\)，故aRah，即ah∈
故aH⊆，又∀b∈，aRb，即\(a^{-1}b∈H\)
故\(b=a(a^{-1}b)∈aH\)
故⊆aH
故=aH，得证
- 商群
由定理四，左陪集{aH}构成G的分类，记商集合G/R=G/H，称为G对H的左商集(所有左陪集的集合)，或左陪集空间。(右商集类似)
考虑整数加法群G和它的子群 H，包含所有 (4) 的倍数的集合。
左商集G/H是由以下四个左陪集构成的集合：
- (0 + 4= {...,-8,-4,0,4,8,...}) 其实就是
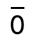(0的等价类集合) - (1 + 4= {...,-7,-3,1,5,9,...}) 其实就是
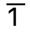(1的等价类集合) - (2 + 4= {...,-6,-2,2,6,10,...}) 其实就是
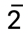(2的等价类集合) - (3 + 4= {...,-5,-1,3,7,11,...}) 其实就是
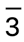(3的等价类集合)
因为超过4会有同余性，所以只有四个左陪集。
推论：对a,b∈G，aH=bH <=> \(a^{-1}b∈H\)
22、定义：设H<G，则|G/H|称为H在G中的指数，记为[G:H]。
示例1、[Z:mZ]=m，m∈IN。 (Z为整数集合，IN为自然数)
∀a∈Z，a+mZ={a+mn|n∈Z}
所有左陪集：,,,...,
，故结论成立
定理六：拉格朗日定理，设G为有限群，H<G，则|G|=[G:H]*|H|
证明：∀a∈G，H->aH，即h|->ah,h∈H，为满射，由消去律，又是单射
故|H|=|aH|
故|G|=[G:H]*|H|，得证
推论：设G为有限群，H<G，K<G，且H⊆K(或H<K)，则
[G:H]=[G:K][K:H]
证明：由拉格朗日定理，
|G|=[G:K]|K|=[G:K][K:H]|H|
|G|=[G:H]|H|
即[G:K][K:H]|H|=[G:H]|H|
得[G:H]=[G:K][K:H] 得证
设H<G，G/H=G/R，要求R，aRb <=> \(a^{-1}b∈H\)为同余关系。即
\(a_1Rb_1,a_2Rb_2\)=>\(a_1a_2Rb_1b_2\)
\(a_1^{-1}b_1∈H,a_2^{-1}b_2∈H\)=>\(a_2^{-1}a_1^{-1}b_1b_2∈H\)
23、定义：设G为群，H<G， 若∀g∈G，h∈H，\(ghg^{-1}∈H\)，称H为G的正规子群，记为H⊴G
示例2：平凡子群必为正规子群。
示例3：若G为Abel群，则任何子群都是正规子群。
示例4：SL(V)⊴GL(V)
\(|ABA^{-1}|=|A||B||A^{-1}|=|A||A^{-1}||B|=|B|\)
定理七：设H<G，则下列条件等价：
- H⊴G
- ∀g∈G，gH=Hg
- \(∀g_1,g_2∈G\)，\(g_1H⋅g_2H=g_1g_2H\)(两个左陪集相乘还是一个左陪集)，其中\(g_1H⋅g_2H=\{g_1h_1g_2h_2|h_1,h_2∈H\}\) (对任何非空子集A,B⊆G，AB={ab|a∈A,b∈B})
证明：1->2，对任何的g∈G，h∈H，\(ghg^{-1}∈H\)
记\(ghg^{-1}=h_1\)，则\(gh=h_1g∈Hg\)，故
gH⊆Hg
同样可证Hg⊆gH，故2成立。
2->3，\(∀h_1,h_2∈H\)，\(h_1g_2∈Hg_2=g_2H\)
存在\(h_1'∈H\)，使\(h_1g_2=g_2h_1'\)，故
\(g_1h_1g_2h_2=g_1g_2h_1'h_2∈g_1g_2H\)
故\(g_1H⋅g_2H⊆g_1g_2H\)，又对任何h∈H
\(g_1g_2h=g_1eg_2h∈g_1H⋅g_2H\)
故\(g_1g_2H⊆g_1H⋅g_2H\)，3成立
3->1，H<G，∀g∈G，h∈H
\(ghg^{-1}=ghg^{-1}e∈gH⋅g^{-1}H=gg^{-1}H=eH=H\)
故\(ghg^{-1}∈H\)
故H⊴G，1成立，得证
定理八：设H<G，则等价关系R： aRb <=> \(a^{-1}b∈H\) 是G的同余<=>H⊴G
这时G/H对诱导的运算构成一个群，称为G对H的商群，记为G/H。
证明；若H⊴G，则对任何的\(a_1,a_2,b_1,b_2∈G\)且
\(a_1Rb_1,a_2Rb_2\)即\(a_1^{-1}b_1∈H,a_2^{-1}b_2∈H\)
则\((a_1a_2)^{-1}b_1b_2=a_2^{-1}a_1^{-1}b_1b_2=a_2^{-1}(a_1^{-1}b_1)a_2(a_2^{-1}b_2)\)
因H⊴G，\(a_2^{-1}(a_1^{-1}b_1)a_2∈H\)
故R为同余关系
反之，则∀g∈G，h∈H
因\(g^{-1}(gh)=h∈H\)，ghRg，又\(g^{-1}Rg^{-1}\)
故\(ghg^{-1}Rgg^{-1}\)，即\(ghg^{-1}Re\)
故\(e^{-1}(ghg^{-1})∈H\)即\(ghg^{-1}∈H\)
故H⊴G
设H⊴G，因R是同余关系，G/R=G/H上有诱导运算\(g_1H⋅g_2H=g_1g_2H\)
结合律：
\((g_1H⋅g_2H)⋅g_3H=g_1g_2H⋅g_3H=g_1g_2g_3H\)
\(g_1H⋅(g_2H⋅g_3H)=g_1H⋅g_2g_3H=g_1g_2g_3H\)
结合律成立
左幺元：
eH=H，∀g∈G，eH⋅gH=egH=gH
左幺元eH=H
左逆元：
∀g∈G，\(g^{-1}H⋅gH=g^{-1}gH=eH\)
gH的左逆为\(g^{-1}H\)
群的1，2，3‘，4’都成立，G/H为群，得证
老乡鸡“开源”了 deepin-IDE 终于实现了自举！ 好家伙，腾讯真把 Switch 变成了「思维驰学习机」 腾讯云4月8日故障复盘及情况说明 RustDesk 远程桌面启动重构 Web 客户端 微信基于 SQLite 的开源终端数据库 WCDB 迎来重大升级 TIOBE 4 月榜单：PHP 跌至历史最低点 FFmpeg 之父 Fabrice Bellard 发布音频压缩工具 TSAC 谷歌发布代码大模型 CodeGemma 不要命啦？做的这么好还开源 - 开源图片 & 海报编辑器工具