【数据科学笔记】闵可夫斯基距离(Minkowski Distance)：全面指南

编程语言 2025-04-08 06:07:37 阅读次数: 0

距离度量是数据科学和机器学习算法的基石，它们使得我们能够测量数据点之间的相似性或差异性。本文将深入探讨闵可夫斯基距离的基础、数学特性及其在不同领域的应用。我们将了解它与其他常见距离度量的关系，并通过Python和R的编程实例展示其用法。

无论是开发聚类算法、处理异常检测，还是优化分类模型，理解闵可夫斯基距离都能增强您的数据分析和模型开发方法。

什么是闵可夫斯基距离？

闵可夫斯基距离是在赋范向量空间中使用的一种灵活的距离度量，以德国数学家Hermann 闵可夫斯基的名字命名。它是几种广为人知的距离度量的泛化形式，因此在数学、计算机科学和数据分析等多个领域中占据着核心地位。
在这里插入图片描述

闵可夫斯基距离的核心在于它提供了一种在多维空间中测量两点间距离的方法。它的特别之处在于，通过一个参数p，可以适应不同的问题空间和数据特征。
闵可夫斯基距离的一般公式如下：

$\left( \sum_{i=1}{n} |x_i - y_i|p \right)^{1/p} ]$

其中：

$(x) 和 (y) 是 n 维空间中的两个点$

$\geq 1 )）$

$x_i - y_i| ) 表示x和y在每个维度上的坐标绝对差异$

闵可夫斯基距离之所以有用，主要有两个原因：

首先，它可以根据需要切换到Manhattan距离或Euclidean距离；

其次，它认识到并非所有数据集都适合纯Manhattan距离或纯Euclidean距离，特别是在高维空间中。

在实践中，参数p的选择通常是通过结合训练/测试验证流程来完成的。通过在交叉验证中测试不同的p值，可以确定哪个值为特定数据集提供了最佳的模型性能。

闵可夫斯基距离的工作原理

让我们看看闵可夫斯基距离是如何与其它距离公式相关的，并通过一个例子来加深理解。

其他距离度量的泛化

闵可夫斯基距离公式包含了Manhattan距离、Euclidean距离和Chebyshev距离的公式。

Manhattan距离( p = 1 )：

当p设置为1时，闵可夫斯基距离变为Manhattan距离，也称为城市街区距离或L1范数，用于测量绝对差异的总和。

$D_{Manhattan}(x, y) = \sum_{i=1}^{n} |x_i - y_i| ]$

Euclidean距离( p = 2 )：

当p设置为2时，闵可夫斯基距离变为Euclidean距离，这是最常见的距离度量，表示两点间的直线距离。

$D_{Euclidean}(x, y) = \sqrt{\sum_{i=1}{n} (x_i - y_i)2} ]$

Chebyshev距离（$ p \to \infty $）：当p趋向于无穷大时，闵可夫斯基距离变为Chebyshev距离，也称为棋盘距离，用于测量沿任意维度的最大差异。

$D_{Chebyshev}(x, y) = \max_{i=1}^{n} |x_i - y_i| ]$

示例分析

为了真正理解闵可夫斯基距离的功能和强大之处，我们通过一个具体的例子来看看参数p如何影响多维空间中距离的计算和解释。

假设在二维空间中有两个点：

点A：(2, 3)
点B：(5, 7)

我们将计算这两个点之间的闵可夫斯基距离，尝试不同的p值。

随着p值的变化，闵可夫斯基距离通常会减少，逐渐接近Chebyshev距离。

这是因为较高的p值会给最大的差异赋予更大的权重，而较小的差异则被赋予较少的权重。

下图展示了不同p值下的距离计算情况：

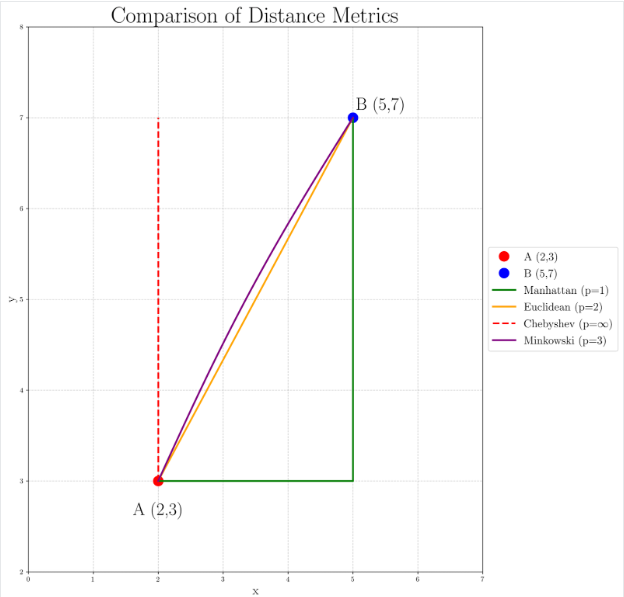
当p=1时，Manhattan距离（绿色路径）是最长的，因为它严格遵循网格。
当p=2时，Euclidean距离（橙色直线）提供了一个直接的直线路径。
当p趋向于无穷大时，Chebyshev距离（红色虚线）只关注最大坐标差异，形成一条先在一个维度上最大化移动再处理另一个维度的路径。
当p=3时，闵可夫斯基距离（紫色曲线）显示出轻微的弯曲，暗示了从Euclidean距离向Chebyshev距离过渡的过程。

这种可视化有助于我们理解为什么在不同的应用场景中可能会选择不同的p值。例如，在城市导航问题中，Manhattan距离可能更合适；而在物理空间计算中，Euclidean距离通常更为常用。对于需要强调较大差异的场景，较高的p值（如p=3的情况）可能是有用的；而当任何维度的最大差异是最重要的因素时，Chebyshev距离可能是首选。

闵可夫斯基距离的应用

闵可夫斯基距离因其可调节的参数p而成为一种灵活的工具，广泛应用于多个领域。通过改变p值，我们可以定制如何测量点之间的距离，使其适用于不同的任务。以下是四个闵可夫斯基距离发挥重要作用的应用场景：

机器学习和数据科学：

在机器学习和数据科学中，闵可夫斯基距离是依赖于测量数据点相似性或差异性的算法的基础。例如，k-最近邻（k-NN）算法就是根据最近邻居的类别来分类数据点。通过使用闵可夫斯基距离，我们可以调整p值来改变“接近度”的计算方式。

模式识别：

模式识别涉及在数据中识别模式和规律，如手写识别或面部特征检测。在这种情况下，闵可夫斯基距离用于测量表示模式的特征向量之间的差异。例如，在图像识别中，每张图像可以用像素值的向量来表示。计算这些向量之间的闵可夫斯基距离可以量化图像之间的相似性或差异性。通过调整p值，我们可以控制距离度量对特定特征差异的敏感度。

异常检测：

异常检测旨在识别与大多数数据点显著偏离的数据点，这对于欺诈检测、网络安全和系统故障检测等领域至关重要。闵可夫斯基距离用于测量数据点与数据集中其他点的距离。距离较大的点可能是潜在的异常值。通过选择合适的p值，分析师可以提高异常检测系统对特定情境下最相关偏差的敏感度。

计算几何和空间分析：

在计算几何和空间分析中，闵可夫斯基距离用于计算空间中点之间的距离，这是许多几何算法的基础。例如，在计算机图形和游戏中的碰撞检测，确定对象是否足够接近以发生交互需要计算它们位置之间的距离。不同p值可以创建不同形状的碰撞边界——从尖锐（较低的p值）到圆滑（较高的p值）。同样，在空间聚类和形状分析中，调整p值可以强调空间关系的不同方面，从城市街区距离到整体形状相似性。

闵可夫斯基距离的数学性质

闵可夫斯基距离不仅在实际应用中是一种灵活的工具，而且在数学理论中也是一个重要的概念，尤其是在度量空间和范数的研究中。

非负性：闵可夫斯基距离总是非负的，即 ( $d(x, y) \geq 0 $)。这是因为它是非负项（绝对值的p次幂）的p次方根。
同一性：闵可夫斯基距离在两个点相同的情况下为零，即 ( $d (x, y) = 0$ ) 当且仅当 ( x = y )。这是因为相同组件之间的绝对差异为零。
对称性：闵可夫斯基距离是对称的，即 ( $d (x, y) = d (y, x)$ )。这是因为绝对值项中的减法顺序不影响结果。
三角不等式：闵可夫斯基距离满足三角不等式，即对于任何三个点 ( x, y, z )，有 ( $\geq d(x, z)$ )。

这些性质确保了闵可夫斯基距离在度量空间中是一个有效的度量函数，使其在理论上和实践中都具有重要意义。

使用Python和R计算Minkowski距离

Python示例

在Python中，我们可以使用SciPy库来计算Minkowski距离，因为该库提供了多种距离度量的有效实现。以下是一个示例，演示了如何为不同的p值计算Minkowski距离：

import numpy as np
from scipy.spatial import distance

# 示例点
point_a = [2, 3]
point_b = [5, 7]

# 不同的p值
p_values = [1, 2, 3, 10, np.inf]
print("Minkowski distances using SciPy:")

for p in p_values:
    if np.isinf(p):
        # 对于p = ∞，使用Chebyshev距离
        dist = distance.chebyshev(point_a, point_b)
        print(f"p = ∞, Distance = {
      
      dist:.2f}")
    else:
        dist = distance.minkowski(point_a, point_b, p)
        print(f"p = {
      
      p}, Distance = {
      
      dist:.2f}")

运行此代码后，可以观察到随着不同p值的变化，距离是如何变化的，这有助于巩固前面文章中讨论的概念。

输出结果如下：

Minkowski distances using SciPy:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

这段代码展示了：

如何使用SciPy的distance函数来计算Minkowski和Chebyshev距离。
如何计算各种p值（包括无穷大）下的距离。
Minkowski距离与其他度量（Manhattan、Euclidean、Chebyshev）之间的关系。

R示例

在R中，我们可以使用stats库中的dist()函数来计算Minkowski距离。以下是示例代码：

# 定义Minkowski距离函数
minkowski_distance <- function(x, y, p) {
    
    
  points <- rbind(x, y)
  if (is.infinite(p)) {
    
    
    # 对于p = Inf，使用method = "maximum"来计算Chebyshev距离
    distance <- stats::dist(points, method = "maximum")
  } else {
    
    
    distance <- stats::dist(points, method = "minkowski", p = p)
  }
  return(as.numeric(distance))
}

# 示例点
point_a <- c(2, 3)
point_b <- c(5, 7)

# 不同的p值
p_values <- c(1, 2, 3, 10, Inf)
cat("Minkowski distances between points A and B using stats::dist:\n")

for (p in p_values) {
    
    
  distance <- minkowski_distance(point_a, point_b, p)
  if (is.infinite(p)) {
    
    
    cat(sprintf("p = ∞, Distance = %.2f\n", distance))
  } else {
    
    
    cat(sprintf("p = %g, Distance = %.2f\n", p, distance))
  }
}

运行此代码后，输出结果如下：

Minkowski distances between points A and B using stats::dist:
p = 1, Distance = 7.00
p = 2, Distance = 5.00
p = 3, Distance = 4.50
p = 10, Distance = 4.02
p = ∞, Distance = 4.00

这段代码展示了：