这个题可以看作用一些路径对网格进行覆盖,那么建图的思路也就有了。。
像最小路径覆盖一样拆成出点和入点,然后把原图的边加上去,考虑到奇数只进不出,偶数只出不进,那么把S连向奇数点,把偶数点连向T,配对的问题就解决了。。然后还有用环覆盖的问题。。由于环上的点和路径上的点一样有入有出,所以只要把空点的入点和出点,分别连向S和T就可以了。。
/**
* ┏┓ ┏┓
* ┏┛┗━━━━━━━┛┗━━━┓
* ┃ ┃
* ┃ ━ ┃
* ┃ > < ┃
* ┃ ┃
* ┃... ⌒ ... ┃
* ┃ ┃
* ┗━┓ ┏━┛
* ┃ ┃ Code is far away from bug with the animal protecting
* ┃ ┃ 神兽保佑,代码无bug
* ┃ ┃
* ┃ ┃
* ┃ ┃
* ┃ ┃
* ┃ ┗━━━┓
* ┃ ┣┓
* ┃ ┏┛
* ┗┓┓┏━━━━━━━━┳┓┏┛
* ┃┫┫ ┃┫┫
* ┗┻┛ ┗┻┛
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
#include<cmath>
#include<map>
#include<stack>
#include<set>
#include<bitset>
#include<assert.h>
#define inc(i,l,r) for(int i=l;i<=r;i++)
#define dec(i,l,r) for(int i=l;i>=r;i--)
#define link(x) for(edge *j=h[x];j;j=j->next)
#define mem(a) memset(a,0,sizeof(a))
#define ll long long
#define eps 1e-8
#define succ(x) (1LL<<(x))
#define lowbit(x) (x&(-x))
#define sqr(x) ((x)*(x))
#define mid ((x+y)/2)
#define NM 5005
#define nm 70005
#define N 1000005
#define M(x,y) x=max(x,y)
const double pi=acos(-1);
const ll inf=1e9+7;
using namespace std;
ll read(){
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
return f*x;
}
struct edge{int t,w,v;edge*next,*rev;}e[nm],*h[NM],*o=e,*p[NM];
void _add(int x,int y,int w,int v){o->v=v;o->w=w;o->t=y;o->next=h[x];h[x]=o++;}
void add(int x,int y,int w,int v){_add(x,y,w,v);_add(y,x,0,-v);h[x]->rev=h[y];h[y]->rev=h[x];}
int n,m,tot,b[55][55],a[55][55],w[NM],_t,ca,d[NM],ans,s;
bool v[NM];
queue<int>q;
int spfa(){
inc(i,1,n)d[i]=inf;mem(v);mem(w);
d[0]=0;w[0]=inf;v[0]++;q.push(0);
while(!q.empty()){
int t=q.front();q.pop();v[t]=false;
link(t)if(j->w&&d[j->t]>d[t]+j->v){
d[j->t]=d[t]+j->v;w[j->t]=min(w[t],j->w);p[j->t]=j;
if(!v[j->t])v[j->t]++,q.push(j->t);
}
}
return w[n];
}
int main(){
int _=read();while(_--){
s=ans=tot=0;mem(e);mem(h);o=e;
n=read();m=read();
inc(i,1,n)inc(j,1,m)b[i][j]=++tot,a[i][j]=read();
inc(i,1,n)inc(j,1,m){
if(a[i][j]%2||a[i][j]==0)add(0,b[i][j],1,0),s++;
if(a[i][j]%2==0)add(b[i][j]+tot,tot*2+1,1,0);
}
inc(i,1,n-1)inc(j,1,m){_t=read();add(b[i][j],b[i+1][j]+tot,1,_t);add(b[i+1][j],b[i][j]+tot,1,_t);}
inc(i,1,n)inc(j,1,m-1){_t=read();add(b[i][j],b[i][j+1]+tot,1,_t);add(b[i][j+1],b[i][j]+tot,1,_t);}
n=2*tot+1;
while(spfa()){
ans+=w[n]*d[n];s-=w[n];
for(int x=n;p[x];x=p[x]->rev->t)p[x]->w-=w[n],p[x]->rev->w+=w[n];
}
if(s)printf("Case #%d: -1\n",++ca);else printf("Case #%d: %d\n",++ca,ans);
}
return 0;
}
Number Link
Time Limit: 12000/6000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 312 Accepted Submission(s): 139
Problem Description
Number Link is a famous game available in platforms including iOS and Android. Given a board with n rows and m columns, the target of the game is to connect pairs of grids with the same numbers. Once two numbers are paired, the path connecting them will occupy the corresponding grids. The path can only go vertically or horizontally. Note that, no two paths could intersect (by sharing the same grid) in any grid. In this problem, you are going to play a modified version, called Number Link ++. See the picture below for an example.
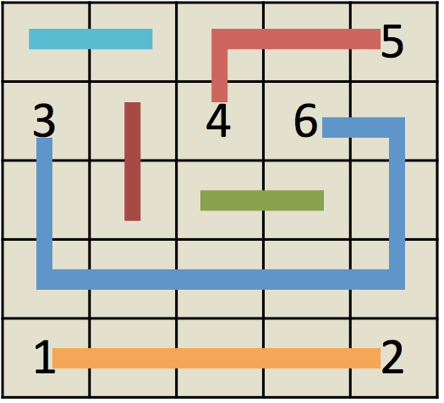
In this new game, you can use two types of paths. Type I is to connect two number grids with different parities (i.e., connect odd number with any other even number). It might be hard to cover the entire grid with only type I path, so we allow type II path, which is a circle path covers only the empty grids (the only special case of type II path is a path only connecting two adjacent empty grids; see the figure above). Since there is no free lunch, we have no free path either. When goes from grid (a,b) to an adjacent grid (c,d), you have to pay for a certain amount of tolls. The cost is the same when goes back from (c,d) to (a,b). Usually the cost of a path is the sum of tolls you paid by traveling along the grids on this path. The only exception is for the special case of type II path. In that case, you have to pay twice the cost (since it is a circle).
The total cost of the game is the sum of costs for all the paths. Can you help me figure out the paths so that each grid is on exactly one path? If there exists such solution, what is the minimum possible cost?
Input
The first line of input consists of an integer T, which is the number of test cases.
Each case begins with two integers, n and m, in a line (1≤n,m≤50).
The next n lines describe the board. Each line consists of m nonnegative numbers, which describe the status of each column from left to right. If the number is zero, then the grid is empty; otherwise it indicates the number on the corresponding grid.
The next n−1 lines each have m nonnegative numbers, which describe the cost of vertical connection. The j-th number in i-th line is the cost when travels from grid (i,j) to (i+1,j).
The next n lines each have m−1 nonnegative numbers, which describe the cost of horizontal connection. The j-th number in i-th line is the cost for a path to go from grid (i,j) to (i,j+1).
All the numbers, including the answer, can be represented using 32-bit signed integer.
Output
For each test case, first output the case number, then output a single number, which is the minimum cost possible to finish the game. When there is no solution available, simply output -1.
Sample Input
3 3 3 1 0 0 1 0 0 2 0 2 1 2 1 2 1 1 3 1 5 6 1 4 1 4 1 1 2 2 1 2 3 3 5 0 0 0 0 0 0 5 0 6 0 0 0 0 0 0 1 1000 1000 1000 1 1 1000 1000 1000 1 1 1 1 1 1000 1 1 1000 1 1 1 1
Sample Output
Case #1: 10 Case #2: -1 Case #3: 14
Hint
Below are the solutions corresponding to case 1 and case 3 respectively. In case 1, you should double pay the red path, since it is a special case of type II path. 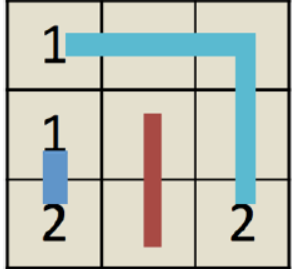
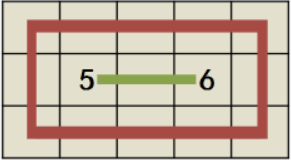
Source
2015ACM/ICPC亚洲区沈阳站-重现赛(感谢东北大学)
Recommend
wange2014 | We have carefully selected several similar problems for you: 6447 6446 6445 6444 6443