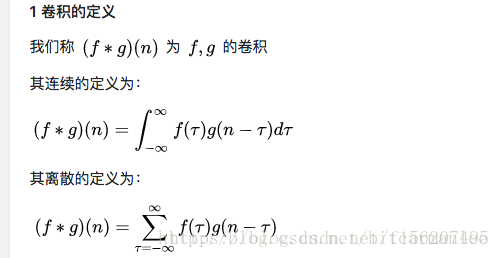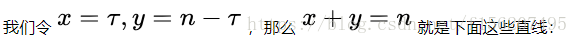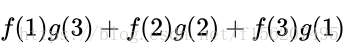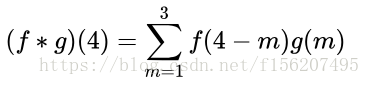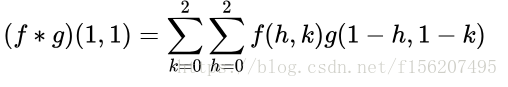用生动的例子来解释卷积

前言

学了几周的深度学习，前几天感觉基础不太牢固，于是今天便从卷积神经网络开始复习，把脑子中不太清楚的概念全部弄清楚。先在这里说清楚，本文大部分例子都是参考其他的博客，在某些例子中有些许改动，穿插着我自己的理解。

1. 从卷毛巾开始理解卷积

首先看看卷积的定义：

这两个定义都有一个共同的特征：

让n不断变化，得到下面动图里面的直线：

如果遍历这些直线，就好比，把毛巾沿着角卷起来并积分（也相当于求和）：

2. 借助信号系统来理解上面的卷积

其实我也没有学过信号系统，不过就常识来讲，系统的响应强度不仅与当前时间t的输入有关，还与前几个时刻 $t-1,t-2$等若干个时刻的输入有关。

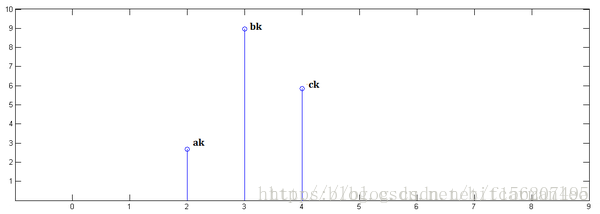
举一个例子：假设任一时刻 $t_{0}$的输入不仅会影响到 $t_{0}$的系统响应强度，而且还会影响后面两个时刻 $t_{1}和t_{2}$的系统响应强度，并且影响权重分别为{a，b，c}，现在分别给出 $t_{0}、t_{1}、t_{2}$时刻的输入为 $i,j,k$，那么如何求出 $t_{0}、t_{1} 、t_{2}、t_{3}、t_{4}$时刻系统的响应强度呢？

其实这个和上面讲到的卷毛巾例子就很像，每一时刻的输入会和后面的输入产生叠加效应。下面给出几张图代表求解过程。

第一步：
$(f*g)(0) = f(0)*g(0-0)$，即 $i*a=ai$；
$(f*g)(1) = f(0)*g(1-0)$，即 $i*b=bi$；
$(f*g)(2) = f(0)*g(2-0)$，即 $i*c=ci$；

第二步：
$(f*g)(1) = f(1)*g(1-1)$，即 $j*a=aj$；
$(f*g)(2) = f(1)*g(2-1)$，即 $j*b=bj$；
$(f*g)(3) = f(1)*g(3-1)$，即 $j*c=cj$；

第三步：
$(f*g)(2) = f(2)*g(2-2)$，即 $k*a=ak$；
$(f*g)(3) = f(2)*g(3-2)$，即 $k*b=bk$；
$(f*g)(4) = f(2)*g(4-2)$，即 $k*c=ck$；

第四步：
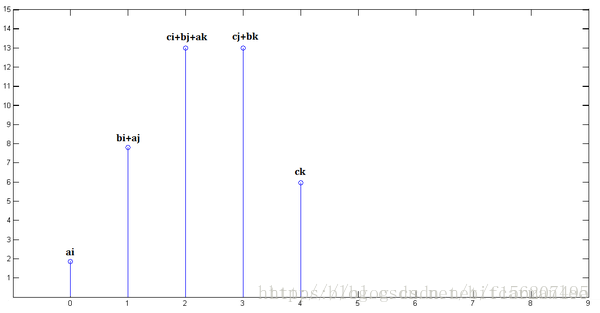
最后将各个时刻的结果累加起来就得到了下面的图

相信你们看了这个例子之后会对前面的卷积公式有很好的理解。从上面那个例子来讲，卷积就是将各个不同时刻输入对某一时刻产生不同的影响叠加的过程。

3. 更多的例子

投骰子
假设我有两枚骰子：

把这两枚骰子都抛出去

求：

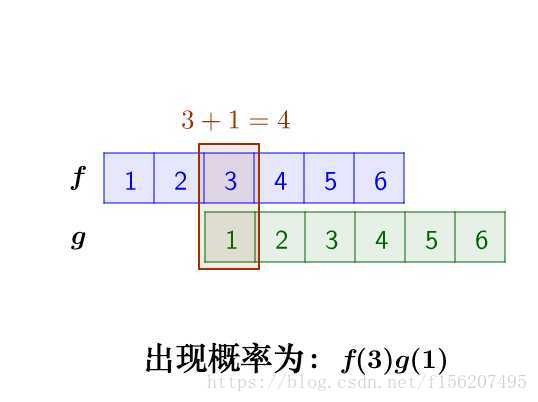
这里问题的关键是，两个骰子加起来要等于4，这正是卷积的应用场景。
我们把骰子各个点数出现的概率表示出来：

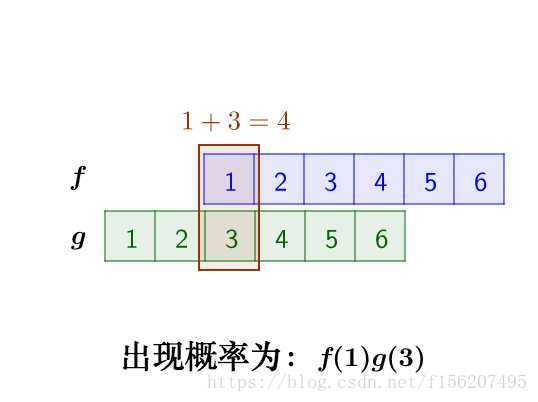
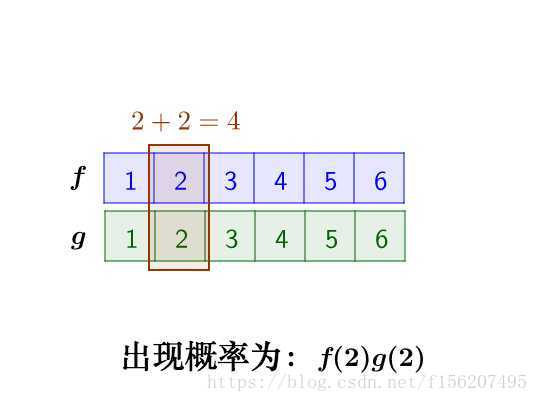
那么，两枚骰子点数加起来为4的情况有

因此，两枚骰子点数加起来为4的概率为：

符合卷积的定义，把它写成标准的形式就是：

做馒头

钻木取火

在生活当中有很多现象都体现了卷积的含义，比如古人钻木取火就是一个很形象的例子。当我们用一根木头与另一根木头接触并钻一下，由于摩擦产生热，在两根木头接触的地方就会发热，但是很明显，就只钻一下，木头是不可能燃起来的，而且随着时间变长，那一点由摩擦产生的热量会一点一点消失掉。妙果我们加快钻的频率，也就是在之前所钻出来的热量还没有消失掉的时候再多钻几下，把之前所有的残余的热量叠加起来，时间越短，残余的热量就会越多，这样热量就会在发热的地方积累得很多，木头的温度也就会越来越高，最后达到着火点而燃烧起来。对于这个例子，其中有几个关键的地方，第一，每一次钻出来的热量消失的速度快慢是由环境客观条件比如温度，和木头的导热系数所决定的。第二，我们认定木头是一个线性系统，也就是对于几任意两次钻的过程互不影响，只存在叠加关系。而且对于每一次不同程度的钻所产生的热量是与钻的程度成正比的。

我们可以把这个问题抽象为一个数学模型：

钻的过程为输入x(t), 系统的衰减函数为h(t),木头被钻的地方积累的热量为y(t)。在某个时间点u，钻所产生的输入为x(u)，此时的衰减系数为h(t-u)为什么是t-u呢？衰减函数接受的参数是经历的衰减时间，从u到t还要经历t-u这么长时间的衰减，所以就要用t-u了，对x(u)h(t-u)du做个积分就得到y(t) 了。

也就是卷积表达了系统对于输入的累计效应。

图像处理

4.1 原理：
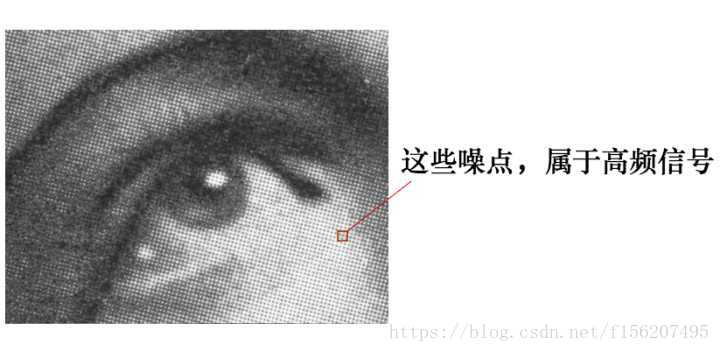
有这么一副图像，可以看到，图像上有很多噪点：

高频信号，就好像平地耸立的山峰：

看起来很显眼。

平滑这座山峰的办法之一就是，把山峰刨掉一些土，填到山峰周围去。用数学的话来说，就是把山峰周围的高度平均一下。

平滑后得到：

4.2
卷积可以帮助实现这个平滑算法。

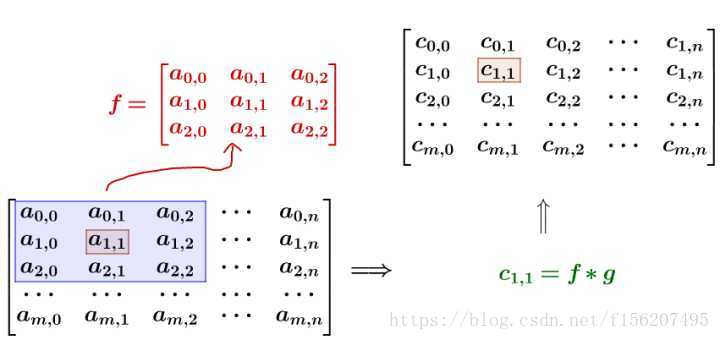
有噪点的原图，可以把它转为一个矩阵：

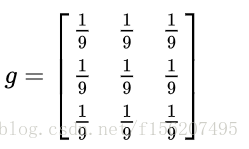
然后用下面这个平均矩阵（说明下，原图的处理实际上用的是正态分布矩阵，这里为了简单，就用了算术平均矩阵）来平滑图像：

记得刚才说过的算法，把高频信号与周围的数值平均一下就可以平滑山峰。

比如我要平滑 $a_{1,1}$ 点，就在矩阵中，取出 $a_{1,1}$ 点附近的点组成矩阵 $f$ ，和 $g$ 进行卷积计算后，再填回去：

要注意一点，为了运用卷积， g 虽然和 f 同维度，但下标有点不一样：

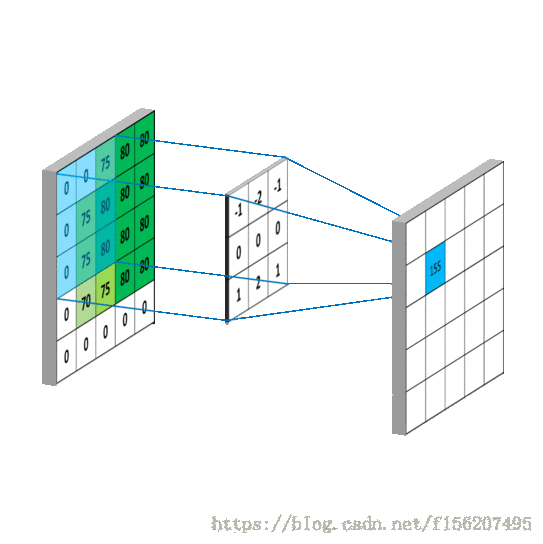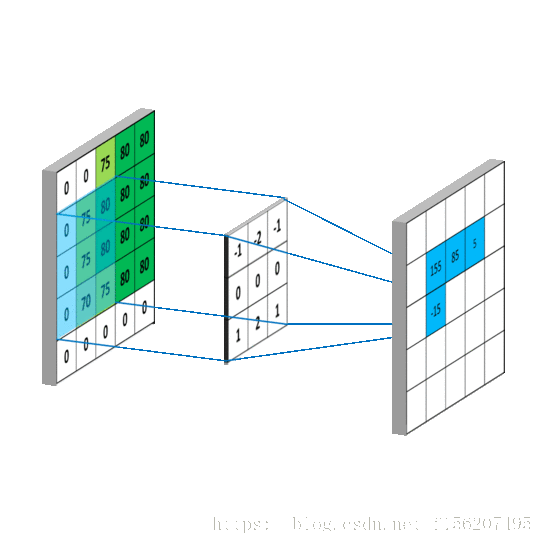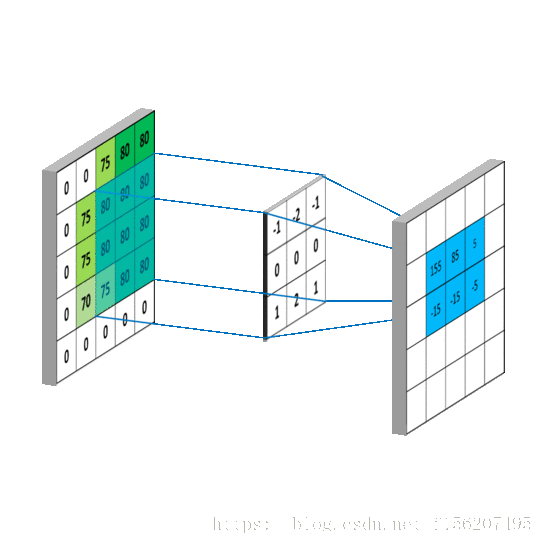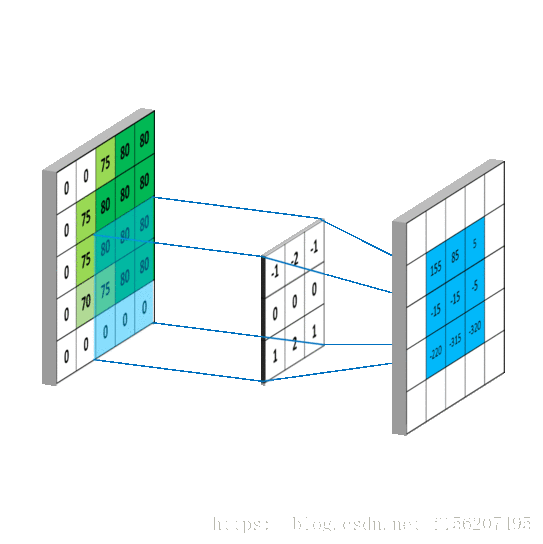
我用一个动图来说明下计算过程：

写成卷积公式就是：

要求 $c_{4,5}$ ，一样可以套用上面的卷积公式。

这样相当于实现了 $g$ 这个矩阵在原来图像上的划动（准确来说，下面这幅图把 g 矩阵旋转了 $180^\circ$ ）：

4. 另外一个关于卷积的有意思的解释

看了好多关于卷积的答案，看到这个例子才彻底地理解了这个过程～
关于卷积的一个血腥的讲解
比如说你的老板命令你干活，你却到楼下打台球去了，后来被老板发现，他非常气愤，扇了你一巴掌（注意，这就是输入信号，脉冲），于是你的脸上会渐渐地（贱贱地）鼓起来一个包，你的脸就是一个系统，而鼓起来的包就是你的脸对巴掌的响应，好，这样就和信号系统建立起来意义对应的联系。下面还需要一些假设来保证论证的严谨：假定你的脸是线性时不变系统，也就是说，无论什么时候老板打你一巴掌，打在你脸的同一位置（这似乎要求你的脸足够光滑，如果你说你长了很多青春痘，甚至整个脸皮处处连续处处不可导，那难度太大了，我就无话可说了哈哈），你的脸上总是会在相同的时间间隔内鼓起来一个相同高度的包来，并且假定以鼓起来的包的大小作为系统输出。好了，那么，下面可以进入核心内容——卷积了！
如果你每天都到地下去打台球，那么老板每天都要扇你一巴掌，不过当老板打你一巴掌后，你5分钟就消肿了，所以时间长了，你甚至就适应这种生活了……如果有一天，老板忍无可忍，以0.5秒的间隔开始不间断的扇你的过程，这样问题就来了，第一次扇你鼓起来的包还没消肿，第二个巴掌就来了，你脸上的包就可能鼓起来两倍高，老板不断扇你，脉冲不断作用在你脸上，效果不断叠加了，这样这些效果就可以求和了，结果就是你脸上的包的高度随时间变化的一个函数了（注意理解）；如果老板再狠一点，频率越来越高，以至于你都辨别不清时间间隔了，那么，求和就变成积分了。可以这样理解，在这个过程中的某一固定的时刻，你的脸上的包的鼓起程度和什么有关呢？和之前每次打你都有关！但是各次的贡献是不一样的，越早打的巴掌，贡献越小，所以这就是说，某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的输出，然后再把不同时刻的输出点放在一起，形成一个函数，这就是卷积，卷积之后的函数就是你脸上的包的大小随时间变化的函数。本来你的包几分钟就可以消肿，可是如果连续打，几个小时也消不了肿了，这难道不是一种平滑过程么？反映到剑桥大学的公式上，f(a)就是第a个巴掌，g(x-a)就是第a个巴掌在x时刻的作用程度，乘起来再叠加就ok了，大家说是不是这个道理呢？我想这个例子已经非常形象了，你对卷积有了更加具体深刻的了解了吗？

参考：

https://www.cnblogs.com/sevenyuan/p/7810755.html
https://www.cnblogs.com/whyandinside/archive/2011/04/17/2019005.html
https://blog.csdn.net/bitcarmanlee/article/details/54729807#comments