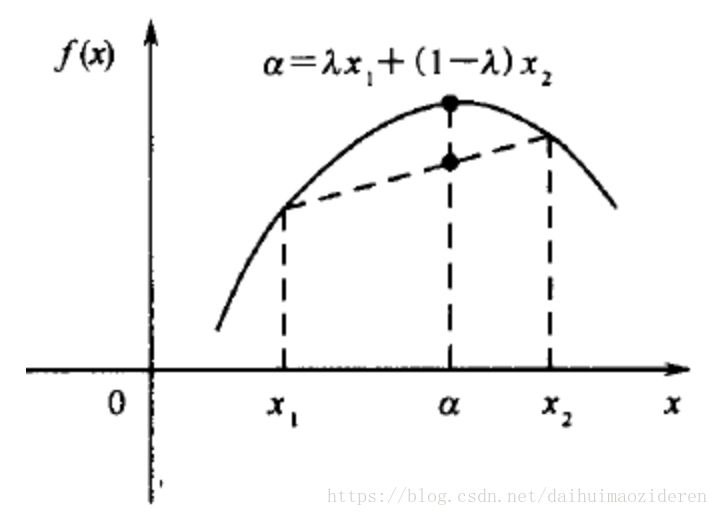版权声明:本文为博主原创文章,未经博主允许不得转载。 https://blog.csdn.net/daihuimaozideren/article/details/81032928
1.导数
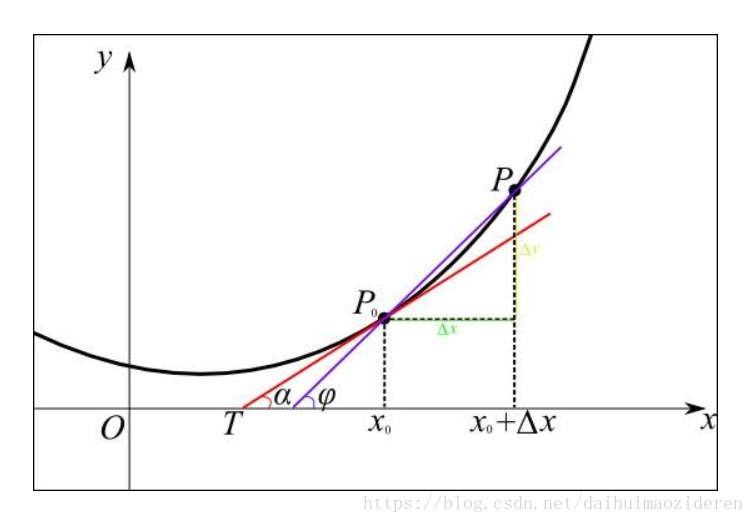
从一元函数图像上看,某一点的导数,即曲线在该点的切线。
一个函数在某一点的导数,描述了这个函数在这一点附近的变化率。
当函数f(x)的自变量,在一点x上产生了一个增量h,若因变量的增量与自变量h的比值,在h趋于0时的极限如果存在,那该比值即为f(x)在点x处的导数。
这里要注意一下几点
(1)不是所有的函数都是可导的。
(2)可导的函数一定是连续的。
(3)不连续的函数一定不可导。
2.偏导数
3.凸凹函数
函数f(x)在某一区间上是连续的。若在该区间内的任意两点,
,其中
,使得
成立,
其中,那么,我们称函数f(x)是该区域上的凸函数。
相反,若使得
成立,
那么,我们称函数f(x)是该区域上的凹函数。
例如,时,
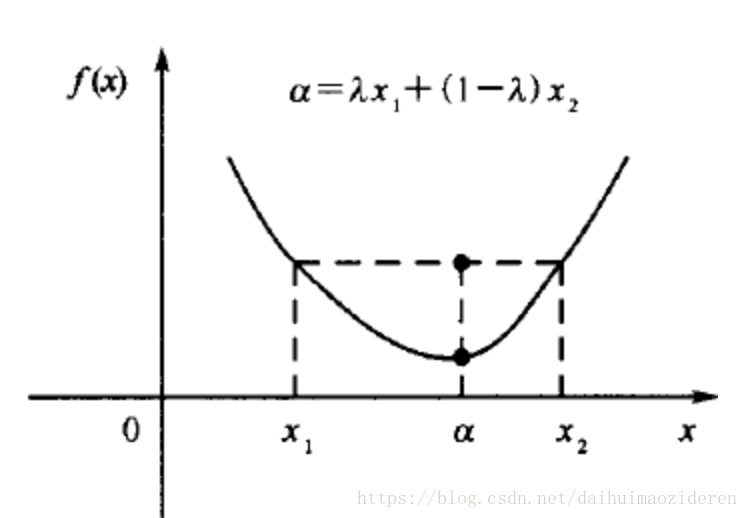
连续函数f(x)称为凸函数的条件为:
即,由点与点
连成的线段的中心点,位于点
的下方。
连续函数f(x)称为凹函数的条件为:
即,由点与点
连成的线段的中心点,位于点
的上方。
若连续函数f(X)在某一区间内,即非凸函数,又非凹函数,那么连续函数f(x)在该区域会存在多个局部最小值(波谷),或多个局部最大值(波峰)。