一、分而治之的思想

分而治之方法与软件设计的模块化方法非常相似
分而治之通常不用于解决问题的小实例，而要解决一个问题的大实例。一般步骤为：
- ①把一个大实例分为两个或多个更小的实例
- ②分别解决每个小实例
- ③把这些小实例的解组合成原始大实例的解

二、实际应用之找出假币

问题描述

一个袋子有16个硬币，其中只有一个是假币，这个假币比其他的真币重量轻（其他所有真币的重量都是相同的），现在要找出这个假币

普通的解决方法

一般的方法就是逐个的进行比较，一旦遇到质量比较轻的就找到假币了

步骤为：

①比较硬币1与硬币2，如果某个硬币比较轻，那么这个轻的硬币就是假币，终止寻找；否则进行下一步

②继续比较硬币2与硬币3，如果某个硬币比较轻，那么这个轻的硬币就是假币，终止寻找；否则进行下一步

......以此类推，直到找到假币终止寻找

分而治之的解决方法

分而治之的思想是把一个问题的大实例分解为两个或更多的小实例，然后进行比较

此处我们将大实例分解为两个小实例，步骤为：

①把16个硬币分为两组A和B，每组8个硬币，计算每组硬币的总质量并进行比较，较轻的那一组肯定含有假币

②将较轻的那一组继续分组，分为A和B，每组4个硬币，然后计算每组硬币的总质量并进行比较，同理，较轻的那一组肯定含有假币

③将较轻的那一组继续分组，分为A和B，每组2个硬币，然后计算每组硬币的总质量并进行比较，同理，较轻的那一组肯定含有假币

④最终只剩下两个硬币，因此不需要再进行分组了，直接比较，较轻的那一个硬币肯定是假币

三、实际应用之金块问题

问题描述

一个老板有一袋金块，每块金块的重量都不同，现在想要找出最重的那个金块与最轻的那个金块

普通的解决方法

普通的解决办法就是逐个比较，找出最重和最轻的金块

步骤一般为：

假设金块的总数为n

先逐个比较每个金块，找出最重的金块

找出最重的金块之后，从剩余的n-1个金块中再找出最轻的金块

比较次数：因为找出最重的金块的比较次数为n-1次，从剩余的金块中再找出最轻的金块用了n-2次，所以总的比较次数为2n-3
template<typename T>
bool find_max_min(T arr[], int n,int &maxIndex,int &minIndex)
{
    if (n <= 0)
        return false;

    //先找出最大的
    maxIndex = 0;
    for (int i = 1; i < n; ++i) {
        if (arr[maxIndex] < arr[i])
            maxIndex = i;
    }

    //再从剩余的当中找出最小的
    minIndex = 0;
    for (int j = 1; j < n; j++) {
        if (j == maxIndex)
            continue;
        if (arr[minIndex] > arr[j])
            minIndex = j;
    }
    
    return true;
}


int main()
{
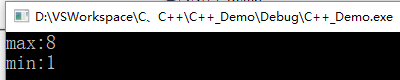
    int arr[] = { 1,4,2,5,1,8,5 };
    int maxIndex, minIndex;

    if (find_max_min(arr, sizeof(arr) / sizeof(int), maxIndex, minIndex)) {
        std::cout << "max:" << arr[maxIndex] << endl;
        std::cout << "min:" << arr[minIndex] << endl;
    }

    return 0;
}

分而治之的解决方法

当n<=2时，一次比较就足够了

当n>2时，总体步骤如下：

①将金块分为A和B两个部分

②分别找出A和B中最重的和最轻的，设A中最重和最轻的金块分别为Ha和La，A中最重和最轻的金块分别为Hb和Lb（这一步可以使用递归来实现）

③比较Ha与Hb就可以找出最重的，比较La与Lb就可以找出最轻的

演示案例：

①假设n=8，有8块金块

②将8个金块分为两个部分A和B，各有4个金块

③因为A中有4个金块，我们将其再分为两个部分A1和A2，每个部分有2个金块

然后通过一次比较可以找出A1中较重的金块Ha1和La1

再通过一次比较可以找出A2中较轻的金块Ha2和La2

然后再通过一次比较Ha1与Ha2找出A中最重的金块Ha，通过一次比较La1与La2找出A中最轻的金块La

④因为B中有4个金块，我们将其再分为两个部分B1和B2，每个部分有2个金块

然后通过一次比较可以找出B1中较重的金块Hb1和Lb1

再通过一次比较可以找出B2中较轻的金块Hb2和Lb2

然后再通过一次比较Hb1与Hb2找出A中最重的金块Hb，通过一次比较Lb1与Lb2找出A中最轻的金块Lb

⑤最后进行一次比较Ha和Hb找出最重的金块，再进行一次比较La和Lb找出最轻的金块。步骤结束

可以看出在上面的分而治之中总共需要比较10次

设c(n)为所需要的比较次数。为了方便，假设n是2的幂：

如果是分而治之法：当n=2时，c(n)=1；对于较大的n，c(n)=2c(n/2)+2

如果是逐个比较方法：c(n)=3n/2-2

因此，使用分而治之方法比逐个比较的方法少用了25%的比较次数

分而治之编码实现

如果使用递归，则步骤如下：

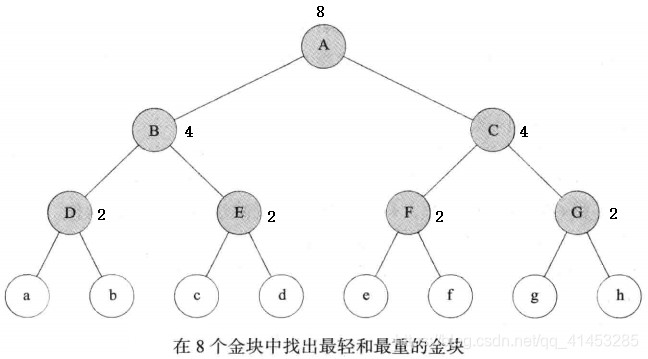
①在上图的二叉树中，沿着根至叶子的路径，把一个大实例划分成为若干个大小为1或2的小实例

②在每个大小为2的实例中，比较确定哪一个较重和哪一个较轻。在节点D、E、F、G完成这种比较。大小为1的实例只有一个金块，它既是最轻的也是最重的

③对较轻的金块进行比较以确定哪一个最轻，对较重的金块进行比较以确定安一个最重。对节点A、B、C执行这种比较

如果使用非递归的方法，代码如下：

复杂度分析：当n为偶数时，在for循环外部又一次比较，内部有3(n/2-1)次比较。总的比较次数为3n/2。当n为奇数时，在for循环外部没有比较，内部有n(n-1)/2次比较。因此，无论n为奇数或偶数，当n>0时，总的比较次数为[3n/2]-2。这是在最早最大值最小值的算法中，比较次数最少的算法
template<typename T>
bool find_max_min(T arr[], int n,int &maxIndex,int &minIndex)
{
    //如果数组大小小于等于0，直接退出
    if (n <= 0)
        return false;
    //如果只有一个金块，那么它既是最重的也是最轻的
    if (n == 1) {
        maxIndex = minIndex = 0;
        return true;
    }
    //如果金块数量大于等于2，开始下面的部分

    int s = 0;//用于标识比较的开始起点
    if (n % 2 == 1) {
        //如果金块数量为奇数，设定最大索引与最小索引为0，然后从s=1索引处开始进行比较
        maxIndex = minIndex = 0;
        s = 1;
    }
    else {
        //如果金块数量为偶数，从前两个元素中提取出较小元素与较大元素的索引，然后从s=2索引处开始比较
        if (arr[0] > arr[1]) {
            maxIndex = 0;
            minIndex = 1;
        }
        else {
            maxIndex = 1;
            minIndex = 0;
        }
        s = 2;
    }

    //从s开始进行比较，每两个元素比较一次
    for (int index = s; index < n; index += 2) {
        if (arr[index] > arr[index +1]) {
            if (arr[index] > arr[maxIndex])
                maxIndex = index;
            if (arr[index + 1] < arr[minIndex])
                minIndex = index + 1;
        }
        else {
            if (arr[index] < arr[minIndex])
                 minIndex = index;
            if (arr[index + 1] > arr[maxIndex])
                maxIndex = index + 1;
        }
    }

    return true;
}


int main()
{
    int arr[] = { 1,4,2,5,0,1,8,3,8 };
    int maxIndex, minIndex;

    if (find_max_min(arr, sizeof(arr) / sizeof(int), maxIndex, minIndex)) {
        std::cout << "max:" << arr[maxIndex] << endl;
        std::cout << "min:" << arr[minIndex] << endl;
    }

	return 0;
}