
首先考虑1*n的情况。上图:n为偶数4 下图:n为奇数5
对于上图,考虑1和3。1的四个角至少有两个灯。3的四个角至少有两个灯,并且1和3的灯是不可能共用的,因为1 3没有公共定点,所以想要1 3满足条件,最少要4盏灯。不妨让灯出现在上图画圈的地方,发现如果灯这么安装,不仅1 3满足条件,整个1*n的广场都满足条件。推广可得,1*n(n为偶数)的最少灯为n
对于上图,考虑1、3、5。因为1、3、5的灯是不可能共用的,所以想要1 3 5满足条件,最少要6盏灯。不妨让灯出现在上图画圈的地方,发现如果灯这么安装,不仅1 3 5满足条件,整个1*n的广场都满足条件。推广可得,1*n(n为奇数)的最少灯为n+1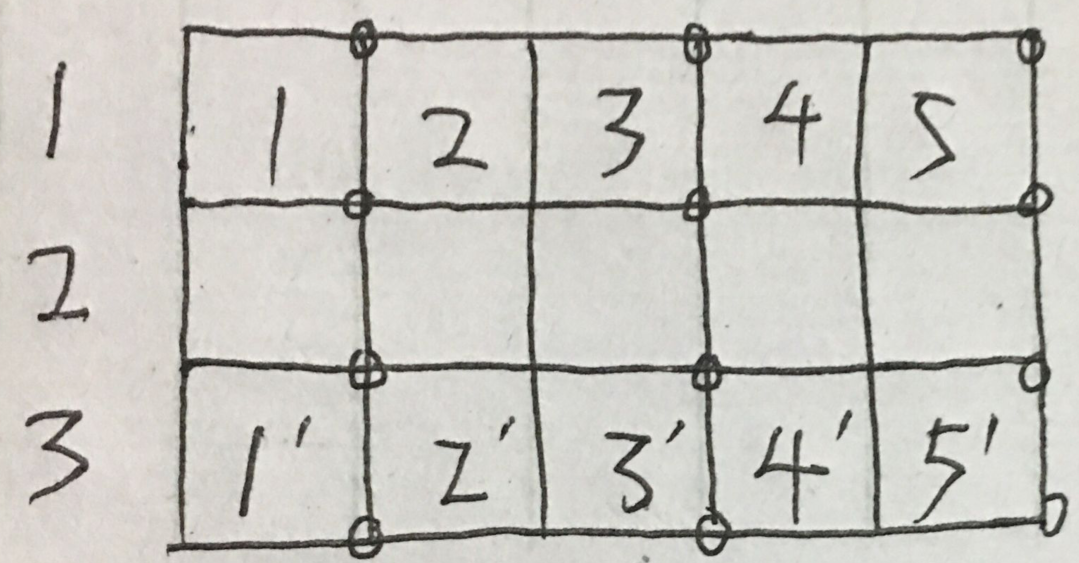
考虑n、m均为奇数的情况。对于1、3行来说,两行没有公共的顶点,所以灯不能共用。对于第1行,想要使该行满足题意,最少需要6个灯,同理,对于3行,也需要6盏灯。所以对于整个广场来说,至少需要12盏灯。当灯的位置如上图圆圈所示时,正好是12盏灯,并且可以让整个广场都满足条件,所以最少灯数就是12。 推广一下,可得当n、m均为奇数时,所需灯最少为(m+1)(n+1) / 2。
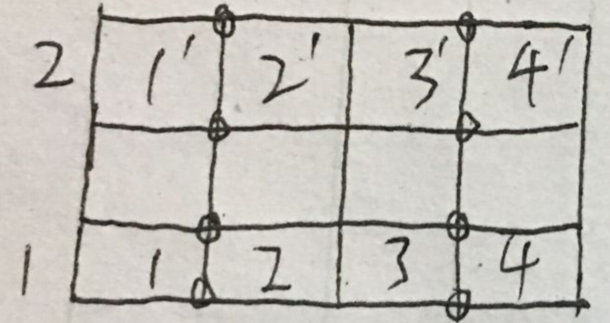
考虑n为偶数m为奇数的情况。对于1、3行来说,两行没有公共的顶点,所以灯不能共用。对于第1行,想要使该行满足题意,最少需要4个灯,同理,对于2行,也需要4盏灯。所以对于整个广场来说,至少需要8盏灯。当灯的位置如上图圆圈所示时,正好是8盏灯,并且可以让整个广场都满足条件,所以最少灯数就是8。 推广一下,可得当n为偶数m为奇数时,所需灯最少为 n(m+1) / 2。

对于n、m全为偶数时,就没那么简单了。如果还按之前的方法,把第1 3列单独考虑,会得到最少的灯数>=4。但实际的最小灯数是5。原因就在于4是偶数,4/2是整数,这就决定了按原来的思想考虑会使某些方块没有两盏灯照。
那对于上图的2*4的矩形,最少的灯数 5 是怎么得到的呢? 假设一个灯在一个方块里产生的亮度为1,所以a、e处的灯产生的亮度都为2,b、c、d产生的亮度为4,大矩形4个顶点处的灯亮度为1。对于上图,一共有8个方块,所以灯需要产生的最小亮度为16。首先考虑第一列,b处必须有灯。因为b点的“功能”最多,“辐射”的范围最广,所以b必须用。下面以8*10的分析一下过程:
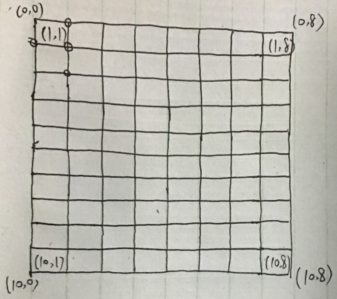
首先考虑左上角的(1,1)方块。该方块的四个角至少有两个点有灯。我先证明在满足题意的安装灯柱最少的安装策略中点1,1处肯定有灯:假设1,1点没灯,那么一共有4种情况,分别是点0,0、点0,1、点1,0有灯;点0,0、点0,1有灯;点1,0、点0,1有灯;点0,0、点1,0有灯;因为0,0点只能照一个方块,与另两个点比毫无优势。并且这三点全亮灯没有其他意义反而多了一盏灯,所以只可能是点1,0、点0,1有灯。我们再引入1,0 1,1亮 0,1、1,1亮两种情况。方案1,0 1,1与1,0 0,1相比,不同点就是0,1 和1,1。点0,1可以让块1,1 1,2亮,点1,1,可以让块1,1 1,2 2,1 2,2亮。所以点1,1的“功能”完全包括了点0,1的“功能”。所以方案1,0 1,1优于方案1,0 0,1。同理方案0,1 1,1优于方案0,1 1,0。但是1,0 1,1与0,1 1,1无法比较好坏。下面我们对这两种方案进行分析。
0,1 、1,0 :

对于2,1方块而言,其四个顶点必然有两个有灯。因为点1,1有灯了,所以要判断剩下三个点里哪个点肯定有灯。因为点2,1功能最多且包括了其他点的功能,所以点2,1是最优点,所以点2,1肯定有灯亮。同理点2,2 、2,3 、 2,4 ···2,10肯定都有灯亮。

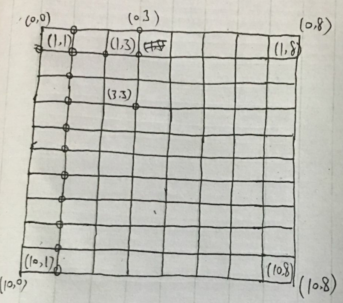
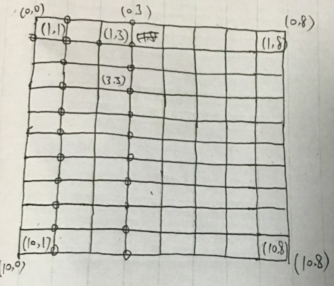
接着分析块1,3 经过和之前类似的分析可知,块1,3有两种方案,一个是点0,3、1,3 另一个是点1,2、 1,3 。我们假设方案点1,2、 1,3优于点0,3、1,3。接下来分析块3,3,对于块3,3而言,候选的方案有点2,3、3,3和点3,2、 3,3假设点2,3、3,3更优。再分析块4,3。可得点4,3必亮灯,继续分析块5,3、···10,3可得点5,3···10,3必亮灯。容易观察得方案点1,2、 1,3差于点0,3、1,3,与“已知”矛盾(此已知不是真正的已知,而是我们假设的已知)。所以假设不成立,所以点3,2、 3,3更优,同理,点5,2 5,3更优、点7,2、7,3 点9,2、 9,3更优。然后再往右走,用同样的判断方法,最后可得到在选择点0,1 1,1 1,2 1,3时最终的方案如下图。
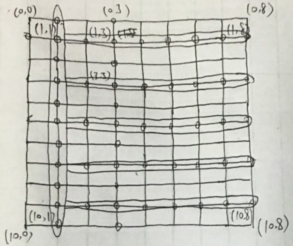
同理可得在选择点0,1 1,1 1,3, 0,3时最终的方案如下图。

从这两种情况就能得到选择点0,1、1,1的最少灯数。 、
方案点1,0 1,1分析方法与点0,1 1,1分析方法相同,在得到 点1,0 1,1的最小灯数后,两者之间的较小值就是最后答案。 推广至n*m n、m均为偶数。最少灯数为 min(n,m)/2*max(n,m)+1
其实可以在一开始就假设点0,1 1,1比点1,0 1,1更优,可直接得到 ,省了中间一大步。但是为了方便自己理解,多讲中间几步也是可以的。
,省了中间一大步。但是为了方便自己理解,多讲中间几步也是可以的。