1.原則
制限付き 3 次スプライン(RCS) は、非線形関係を分析するための最も一般的な方法の 1 つです。RCS は、3 次関数を使用して異なるノード間の曲線をフィッティングし、それらを滑らかに接続します。これにより、曲線全体をフィッティングし、その線形性をテストするプロセスが実現されます。ご想像のとおり、RCS のノード数はフィッティング結果にとって非常に重要です。通常、サンプル数が 30 未満の小規模なサンプルには 3 つのノードが使用され、大きなサンプルには 5 つのノードが使用されます。
2.Rの実施
1.コックスリターン
#Used for RCS(Restricted Cubic Spline)
#我们使用rms包
library(ggplot2)
library(rms)
library(survminer)
library(survival)ここでは、Survival パッケージの肺データを使用します。
#####基于cox回归
#这里用survival包里的lung数据集来做范例分析
head(lung)
# inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
# 3 306 2 74 1 1 90 100 1175 NA
# 3 455 2 68 1 0 90 90 1225 15
# 3 1010 1 56 1 0 90 90 NA 15
# 5 210 2 57 1 1 90 60 1150 11
# 1 883 2 60 1 0 100 90 NA 0
# 12 1022 1 74 1 1 50 80 513 0
#status: censoring status 1=censored, 2=dead
#sex: Male=1 Female=2
#ph.ecog:医生对患者的体能状态评级
#ph.karno:医生对患者的另一种体能状态评级karnofsky
#pat.karno:患者karnofsky自评
#meal.cal:摄入卡路里
#wt.loss:过去半年体重减轻
# 对数据进行打包,整理
dd <- datadist(lung) #为后续程序设定数据环境
options(datadist='dd') #为后续程序设定数据环境
#用AIC法计算不同节点数选择下的模型拟合度来决定最佳节点数
for (knot in 3:10) {
fit <- cph(Surv(time,status) ~ rcs(meal.cal,knot) + sex+age , x=TRUE, y=TRUE,data=lung)
tmp <- extractAIC(fit)
if(knot==3){AIC=tmp[2];nk=3}
if(tmp[2]<AIC){AIC=tmp[2];nk=knot}
}
nk #3
#cox回归中自变量对HR的rcs
fit <- cph(Surv(time,status) ~ rcs(meal.cal,3) + sex+age , x=TRUE, y=TRUE,data=lung)#大样本5节点,小样本(<30)3节点
#比例风险PH假设检验,p>0.05满足假设检验
cox.zph(fit,"rank")
#非线性检验,p<0.05为有非线性关系
anova(fit)
#这里的结果是
# Wald Statistics Response: Surv(time, status)
#
# Factor Chi-Square d.f. P
# meal.cal 0.42 2 0.8113
# Nonlinear 0.09 1 0.7643,呈线性
# sex 6.61 1 0.0101
# age 1.99 1 0.1582
# TOTAL 10.29 4 0.0358
#查看各meal.cal对应的HR值
HR<-Predict(fit, meal.cal,fun=exp)
head(HR)
#画图
ggplot()+
geom_line(data=HR, aes(meal.cal,yhat),
linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+
geom_ribbon(data=HR,
aes(meal.cal,ymin = lower, ymax = upper),
alpha = 0.1,fill="#0070b9")+
theme_classic()+
geom_hline(yintercept=1, linetype=2,size=1)+
labs(title = "Lung Cancer Risk", x="Age", y="HR (95%CI)") 結果は次の図のように描画されます。
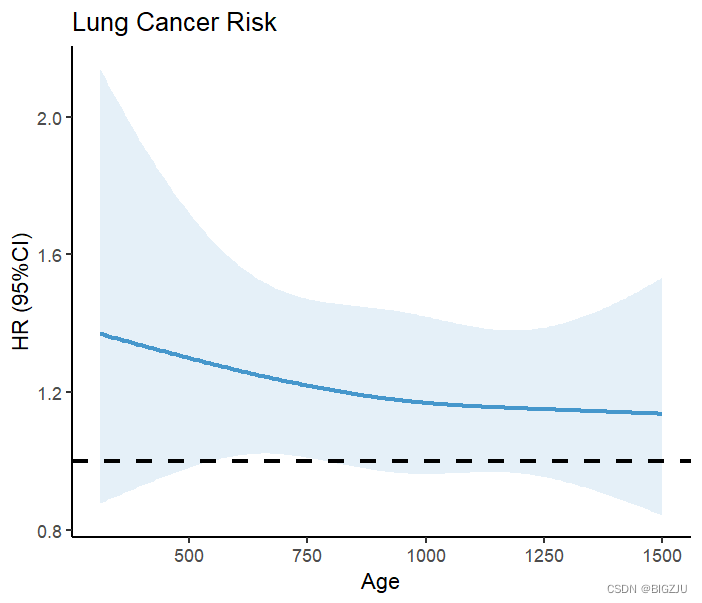
anova(fit) の結果と視覚的表示は、食事エネルギー摂取量と RCS 下の死亡率との間に線形関係があることを示しています。
別の非線形例を見てみましょう。この例では、サバイバル パッケージのコロン データを使用します。
#结肠癌病人数据
Colon <- colon
Colon$sex <- as.factor(Colon$sex)#1 for male,0 for female
Colon$etype <- as.factor(Colon$etype-1)
dd <- datadist(Colon)
options(datadist='dd')
for (knot in 3:10) {
fit <- cph(Surv(time,etype==1) ~ rcs(age,knot) +sex , x=TRUE, y=TRUE,data=Colon)
tmp <- extractAIC(fit)
if(knot==3){AIC=tmp[2];nk1=3}
if(tmp[2]<AIC){AIC=tmp[2];nk1=knot}
}
nk1 #3
fit <- cph(Surv(time,etype==1) ~ rcs(age,3) +sex , x=TRUE, y=TRUE,data=Colon)
cox.zph(fit,"rank")
anova(fit)
# Wald Statistics Response: Surv(time, etype == 1)
#
# Factor Chi-Square d.f. P
# age 6.90 2 0.0317
# Nonlinear 6.32 1 0.0120,非线性
# sex 1.20 1 0.2732
# TOTAL 7.54 3 0.0565
HR<-Predict(fit, age,fun=exp)
head(HR)
ggplot()+
geom_line(data=HR, aes(age,yhat),
linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+
geom_ribbon(data=HR,
aes(age,ymin = lower, ymax = upper),
alpha = 0.1,fill="#0070b9")+
theme_classic()+
geom_hline(yintercept=1, linetype=2,size=1)+
geom_vline(xintercept=47.35176,size=1,color = '#d40e8c')+#查表HR=1对应的age
geom_vline(xintercept=65.26131,size=1,color = '#d40e8c')+
labs(title = "Colon Cancer Risk", x="Age", y="HR (95%CI)") 結果は次のとおりです。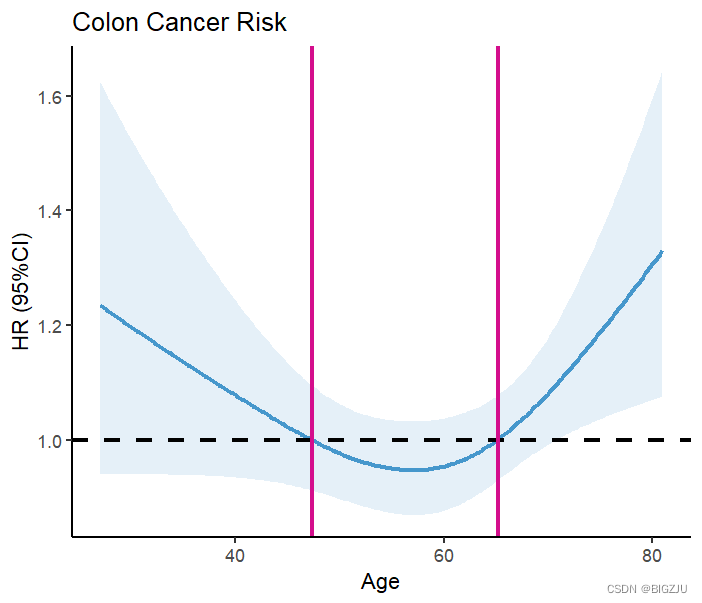
anova(fit) の結果と視覚的プレゼンテーションは、この例が非線形関係を示していることを示しています。
Predict() 関数のパラメータを変更するだけで、グループ化された調査や視覚的なプレゼンテーションを実行することもできます。
HR1 <- Predict(fit, age, sex=c('0','1'),
fun=exp,type="predictions",
conf.int = 0.95,digits =2)
HR1
ggplot()+
geom_line(data=HR1, aes(age,yhat, color = sex),
linetype="solid",size=1,alpha = 0.7)+
geom_ribbon(data=HR1,
aes(age,ymin = lower, ymax = upper,fill = sex),
alpha = 0.1)+
scale_color_manual(values = c('#0070b9','#d40e8c'))+
scale_fill_manual(values = c('#0070b9','#d40e8c'))+
theme_classic()+
geom_hline(yintercept=1, linetype=2,size=1)+
labs(title = "Colon Cancer Risk", x="Age", y="HR (95%CI)")
結果:
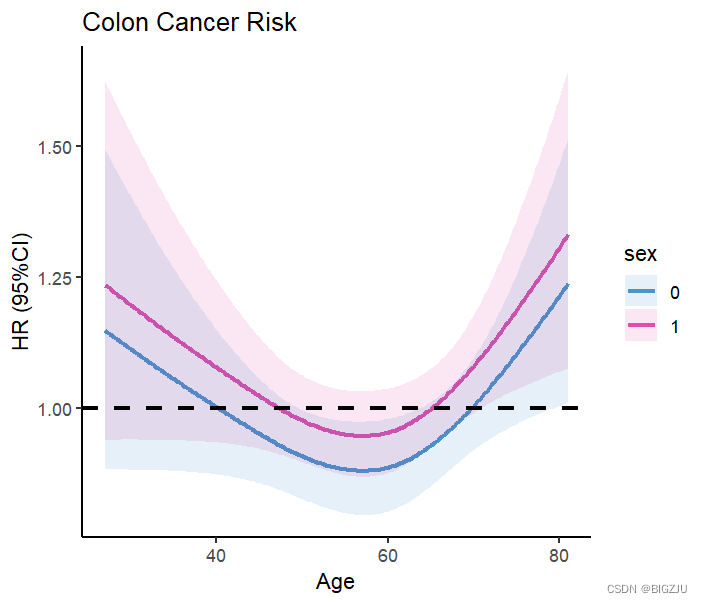
2.ロジスティック回帰
cox 回帰の代わりにロジスティック回帰を使用した場合、全体的な結果はほぼ同じになるため、モデルを置き換えるだけで済みます。
#####基于logistic回归的rcs
#建模型
fit <-lrm(status ~ rcs(age, 3)+sex,data=lung)
OR <- Predict(fit, age,fun=exp)
#画图
ggplot()+
geom_line(data=OR, aes(age,yhat),
linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+
geom_ribbon(data=OR,
aes(age,ymin = lower, ymax = upper),
alpha = 0.1,fill="#0070b9")+
theme_classic()+
geom_hline(yintercept=1, linetype=2,size=1)+
geom_vline(xintercept=38.93970,size=1,color = '#d40e8c')+ #查表OR=1对应的age
labs(title = "Lung Cancer Risk", x="Age", y="OR (95%CI)")3. 線形回帰
線形回帰についても同様です
#####基于线性回归的rcs
fit <- ols(meal.cal ~rcs(age,3)+sex,data=lung)
Kcal <- Predict(fit,age)
#画图
ggplot()+
geom_line(data=Kcal, aes(age,yhat),
linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+
geom_ribbon(data=Kcal,
aes(age,ymin = lower, ymax = upper),
alpha = 0.1,fill="#0070b9")+
theme_classic()+
labs(title = "RCS", x="Age", y="Kcal")