著者:ユー・ファン
背景
人工知能 (AI) の発展により、科学的発見に新しいパラダイムが導入されました。現在、AI は空間的・時間的スケールの広い自然現象を高度化・加速させて理解できるようになり、自然科学の発展を促進し、AI4 サイエンスという新たな研究分野を生み出しています。最近、60 人以上の著者が共同で執筆したレビュー論文「量子、原子、連続システムにおける科学のための人工知能」では、亜原子、原子、および連続システムのサブフィールドに関する詳細な技術概要が提供されています。ここでは、このレビューの技術的バックボーンを抽出し、対称変換の下で等変モデルを構築する方法に焦点を当てます。
1 はじめに
1929 年、量子物理学者のポール ディラックは次のように述べています。「ほとんどの物理学とすべての化学の数学的理論に必要な基本的な物理法則は、すでに完全にわかっていますが、難しいのは、これらの法則を正確に適用することで、複素数 これは、量子物理学のシュレーディンガー方程式から流体力学のナビエ・ストークス方程式まで当てはまります。深層学習により、これらの方程式の解を高速化できます。従来のシミュレーション手法の結果をトレーニング データとして使用し、一度トレーニングすると、これらのモデルは従来のシミュレーションよりもはるかに高速に予測を行うことができます。
生物学などの他の分野では、基礎となる生物物理学的プロセスが完全には理解されていない可能性があり、最終的には数式で説明できない場合があります。このような場合、タンパク質予測モデル AlphaFold、RoseTTAFold、ESMFold、および実験によって得られたその他の 3D 構造など、実験的に生成されたデータを使用して深層学習モデルをトレーニングできるため、コンピューターによって予測されたタンパク質 3D 構造の精度が実験結果と同等になることができます。 。
1.1 科学分野
この記事で関心のある科学分野は、モデル化されている物理システムの空間的および時間的スケールに従って、以下の図の概要として整理されています。
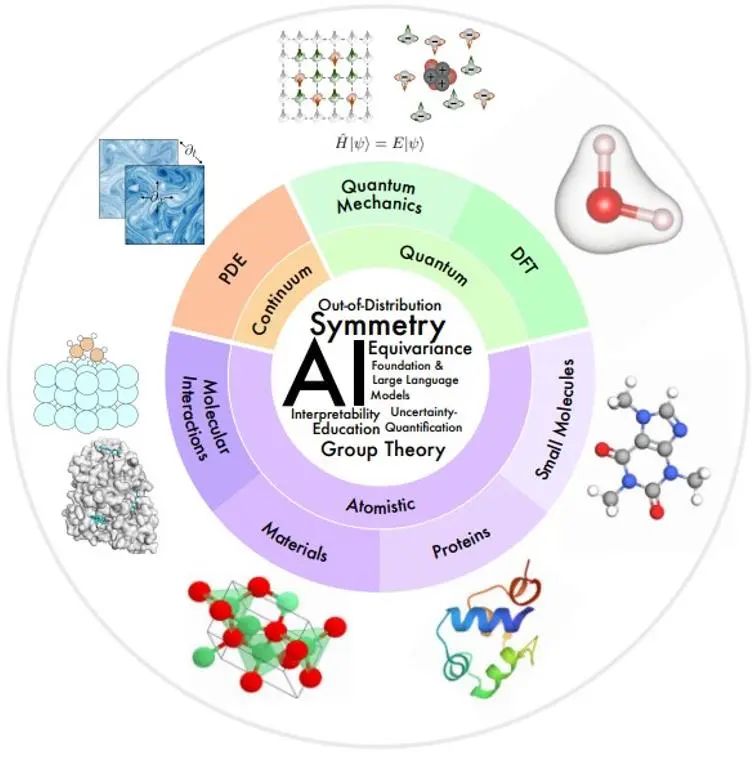
小規模: 量子力学は、波動関数を使用して物理現象を最小スケールで研究します。これに従うシュレーディンガー方程式は、量子系の完全な動的プロセスを記述しますが、指数関数的な複雑さをもたらします。密度汎関数理論(DFT) と非経験量子化学法は、分子や材料の電子構造と物理的特性を計算するために実際に広く使用されている第一原理手法であり、分子や固体の電子的および機械的特性、光学的特性をさらに推定することができます。 、磁気特性と触媒特性。ただし、これらの方法は依然として計算コストが高く、その使用は小規模なシステム (約 1000 原子) に限定されます。 AI モデルは速度と精度の向上に役立ちます。
メソスケール:通常、サイズが数十から数百の原子である小分子は、多くの化学および生物学的プロセスにおいて重要な制御およびシグナル伝達の役割を果たします。タンパク質は、1 つ以上のアミノ酸鎖で構成される大きな分子です。アミノ酸配列はタンパク質の構造を決定し、それが機能を決定します。材料科学の研究では、加工、構造、特性、材料の関係を研究します。分子相互作用では、リガンドと受容体の相互作用や分子と物質の相互作用など、分子相互作用を通じて多くの物理的および生物学的機能がどのように実行されるかを研究します。これらの分野では、AI は分子の特性評価と生成、分子動力学、タンパク質構造の予測と設計、材料特性の予測と構造生成において多くの進歩を遂げています。
大規模: 連続体力学では、偏微分方程式を使用して、流体の流れ、熱伝達、電磁波などを含む、巨視的なレベルで時間と空間で進化する物理プロセスをモデル化します。 AI 手法は、計算効率の向上、一般化、多重解像度解析などの問題に対する解決策を提供します。
1.2 AI技術分野
科学 AI の複数の分野にわたって、共通の技術的課題が存在します。
**対称性:**対称性は非常に強力な帰納的パラノイアであるため、AI4Science の重要な課題は、対称性を AI モデルに効果的に統合する方法です。
**解釈可能性:**AI4Science では、物理世界の法則を理解するために解釈可能性が重要です。
**分布外 (OOD) 一般化と因果関係: **異なる設定ごとにトレーニング データが生成されることを避けるために、OOD 一般化を可能にする因果関係を特定する必要があります。
**基本モデルと大規模言語モデル:**自然言語処理タスクの基本モデルは、自己教師ありまたは一般化可能な教師の下で事前トレーニングされ、さまざまな下流タスクを少数ショットまたはゼロショットで実行します。この記事では、このパラダイムが AI4Science の発見をどのように加速できるかについての展望を提供します。
**不確実性の定量化 (UQ): **データとモデルの不確実性の下で堅牢な意思決定を保証する方法を研究します。
**教育:** 学習と教育を促進するために、この記事では、著者が役立つと考えるリソースの分類されたリストを提供し、コミュニティが AI と科学および教育の統合をより効果的に促進できる方法についての視点を提供します。
**2. **対称性、等価性、およびその理論
多くの科学的問題では、対象となるオブジェクトは通常 3D 空間に位置し、オブジェクトの数学的表現は参照座標系に依存し、そのような表現は座標系に対して相対的に行われます。ただし、座標系は自然界には存在しないため、座標系に依存しない表現が必要です。したがって、AI4Science の重要な課題の 1 つは、座標系変換の下で不変性または等変性をどのように達成するかということです。
2.1 概要
対称性とは、物理現象の特性が、座標変換などの特定の変換のもとでも変化しないという事実を指します。システムに特定の対称性が存在する場合、予測ターゲットは、対応する対称性変換の下では当然不変または等変になります。たとえば、3D 分子のエネルギーを予測する場合、3D 分子が平行移動または回転しても、予測値は変化しません。対称性を意識した学習を実現する別の戦略は、教師あり学習でデータ拡張を使用することです。具体的には、ランダムな対称変換を入力データとラベルに適用して、モデルにほぼ等変な予測を出力させることです。しかし、これには多くの欠点があります。
1) 座標系の選択における追加の自由度を考慮すると、モデルは、固定座標系で元々単純だったパターンを表現するために、より大きな容量を必要とします。
2) 平行移動などの多くの対称変換では、無限の数の等変サンプルが生成される可能性があり、限られたデータ拡張ではデータの対称性を完全に反映することが困難になります。
3) 場合によっては、良好な予測結果を得るために非常に深いモデルを構築する必要があります。モデルの各層が等分散を維持できない場合、全体の等分散の出力を予測することが困難になります。
4) 分子モデリングなどの科学的問題では、機械学習を信頼できる方法で使用できるように、対称変換の下でもロバストな予測を提供することが重要です。
データ拡張には多くの欠点があるため、対称性の要件を満たす機械学習モデルの設計に焦点を当てた研究が増えています。対称適応アーキテクチャの下では、モデルはデータ拡張を行わずに学習ターゲットの予測タスクに集中できます。
2.2 離散対称変換における等価性
このセクションでは、著者は AI モデルにおける離散対称変換の下で等分散を維持する例を示します。この問題例では、ある瞬間から次の瞬間までの 2D 平面内のスカラー流れ場のマッピングをシミュレートします。入力流れ場が 90、180、270 度回転すると、出力流れ場もそれに応じて回転します。その数式は次のとおりです。
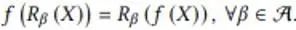
ここで、f は流れ場マッピング関数を表し、R は離散回転変換を表します。 Cohen らは、この問題を解決するために等変グループ畳み込みニューラル ネットワーク (G-CNN) を提案しました。その最も単純な基本コンポーネントは昇順畳み込みです。
1) まず、対称変換ですべての角度でコンボリューション カーネルを回転し、回転されたコンボリューション カーネルを使用して入力に対して対応するコンボリューション演算を実行して、複数の特徴レイヤーを取得し、これらの特徴レイヤーを新しく生成された回転次元 α にスタックします 2。 ) プーリングはこの回転次元 α で実行されるため、入力 X が回転すると、結果として得られる出力は対応する回転を生成します。
プーリング操作の存在により、等変行は維持されますが、これらの特徴は通常、次の図に示すような構造を採用します。
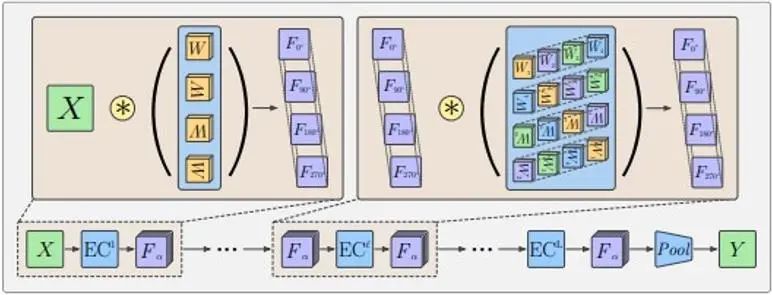
まず、回転畳み込みカーネルを使用して入力の次元を増加させます。次に、多層グループ畳み込み層を使用して、回転次元を維持しながら各機能層が回転等分散性の要件を満たすようにし、最後にプーリング層が使用されます。回転寸法を排除するために使用されます。これにより、中間フィーチャ レイヤーは、フィーチャの相対的な位置と方向のパターンをより適切に検出できるようになります。中間特徴層の等分散の意味は、特徴層が回転変換に応じて回転し、回転次元の順序も回転し、使用されるグループ コンボリューション層内のコンボリューション カーネルの回転と回転の設計も同様になることです。出力フィーチャ レイヤーは、この等分散特性を維持できます。
2.3-2.5 3次元連続変換の等変モデルの構築
多くの科学的問題では、3D 空間における連続的な回転対称と並進対称に焦点を当てます。たとえば、化学分子の構造が回転および並進すると、予測された分子属性で構成されるベクトルは対応する変換を受けます。これらの連続回転変換 R と平行移動変換 t は SE(3) 群の要素を構成し、これらの変換はベクトル空間上の変換行列として表現できます。異なるベクトル空間の変換行列は異なる場合がありますが、これらのベクトル空間は独立したサブベクトル空間に分解できます。各部分空間には同じ変換規則が存在します。つまり、グループ内のすべての変換要素を部分空間のベクトルに適用することによって得られるベクトルは、依然として部分空間内にあります。したがって、グループ内の変換要素は、次のように既約になります。部分空間の変換行列表現。たとえば、総エネルギーやエネルギー ギャップなどのスカラーは、SE(3) 群要素の作用下では変化せず、その変換行列は、SE(3) 群要素の作用下で D^0(R)=1 として表されます。力場などの 3D ベクトル アクションの下で対応する回転が発生し、その変換行列は高次元ベクトル空間では D^1(R)=R として表されます。D^l(R) は 2l+1 です。 -次元正方行列。これらの変換行列 D^l(R) は、回転 R に対応する l 次の Wigner-D 行列と呼ばれ、対応する部分ベクトル空間は SE(3) 群の l 次の既約不変部分空間になり、その中のベクトルは l 次等変ベクトルと呼ばれます。変換変換では、関心のあるプロパティは相対位置にのみ関連するため、これらのベクトルは常に変更されません。
3D 幾何学情報を SE(3) 群の不変部分空間内のフィーチャにマッピングする通常の方法は、球面調和関数マッピングを使用することです。球面調和関数 Y^l は、3 次元ベクトルを 2l+1 次元ベクトルにマッピングします。これは、入力ベクトルが 2l+1 個の基本球面調和関数に分解されるときの係数を表します。下図に示すように、限られた数の基底しか使用しないため、3 次元ベクトルで表される球上のデルタ関数はある程度広がります。

球面調和関数には次の等変特性があります。
このうち、D は前述の l 次 Wigner-D 行列です。したがって、空間関数は、回転変換の下で、異なる次数の等変ベクトルの組み合わせに分解されます。
ノードとして原子座標を持つグラフ ニューラル ネットワークで、ノード特徴 h が次数 l_1 の等変ベクトルであると仮定すると、次のグラフ情報の転送と更新により、更新された h も等変を維持することが保証されます。
この際の重要なステップは、情報転送中のテンソル積演算 (TP) です。このうち、vecは行列をベクトル化することを意味し、係数Cは2l_3+1行(2l_1+1)(2l_2+1)列の行列となる。
ノード特徴量 h は次数 l_1 の既約不変部分空間のベクトルです。エッジ方向 r_ij の球面調和関数 Y は次数 l_2 の既約不変部分空間のベクトルです。これら 2 つのベクトルの直接積によって得られるベクトルです。空間は約分可能であり、係数 C はこの約分可能空間から次数 l_3 の既約不変部分空間への変換関係です。たとえば、2 つの 3 次元ベクトルの直積空間は次のようになります。
直積空間の回転変換行列は、上図の中央にある 3 ブロックの対角行列に変換できます。これは、この空間が 1、3、5 の次元を持つ 3 つの既約不変部分空間に分解できることを意味します。つまり、3⨂ 3=1⊕3⊕5 のベクトル空間の分解です。係数 C は、この 9 次元空間からこれらの 1 次元、3 次元、5 次元空間への変換行列です。上の式では、l_1、l_2、l_3 はすべて 1 つの値のみをとり、次数が固定された等変特徴量です。実際のネットワーク内の特徴量は、これらの異なる次数の特徴量の組み合わせである可能性があります。
2.6-2.7 前の例では、群理論理論と球面調和関数の特性が使用されました。群理論と球面調和関数の基本知識は、この記事のこれら 2 つの章で詳しく紹介されています。
2.8 ステアリング可能なカーネルは等変ネットワークの一般的な形式を構成する
離散および連続変換の下での以前の等変ネットワーク層は、統合変数畳み込み (ステアリング可能な CNN) の形式で記述できます。
このうち、x と y は空間座標、f_in(y) は座標 y の入力特徴ベクトル、f_out(x) は座標 x の出力特徴ベクトル、K は入力特徴空間から出力特徴への変換です。空間。畳み込み演算により並進等分散性が保証されるため、他の空間アフィン変換でも等分散性が保証されます。畳み込みカーネル K は次の対称制約も満たす必要があります。
このうち、g は空間変換グループの変換であり、ρ_in と ρ_out はそれぞれ入力特徴空間と出力特徴空間での変換の表現 (つまり、変換行列) を表します。
この時点で、この記事の対称性と等分散性の理論的説明は基本的に終了し、続いて第 1 章にリストされている複数の分野の個別の概要が説明されます。
参考文献
[1] Ren P、Rao C、Liu Y、他。 PhyCRNet: 時空間偏微分方程式を解くための物理学に基づいた畳み込み再帰型ネットワーク[J]。応用力学および工学におけるコンピュータ手法、2022、389: 114399。
[2] https://www.sciencedirect.com/science/article/abs/pii/S0045782521006514?via%3Dihub
【1】 Xuan Zhang、Limei Wang、Jacob Helwig 他2023年。量子、原子、連続システムにおける科学のための人工知能。 arXiv: https://arxiv.org/abs/2307.08423
【2】タコ・コーエンとマックス・ウェリング。 2016. 群等変畳み込みネットワーク。機械学習に関する国際会議にて。 PMLR、48:2990–2999。
【3】ナサニエル・トーマス、テス・スミット、スティーブン・カーンズほか。 2018. テンソル フィールド ネットワーク: 3D 点群の回転および並進等価ニューラル ネットワーク。 arXiv: https://arxiv.org/abs/1802.08219
モーリス・ワイラー、マリオ・ガイガー、マックス・ウェリング 他2018. 3D ステアリング可能な CNN: ボリューム データの回転等変特徴の学習。神経情報処理システムの進歩
1990 年代生まれのプログラマーがビデオ移植ソフトウェアを開発し、1 年足らずで 700 万以上の利益を上げました。結末は非常に罰的でした。 Google は、Flutter、Dart、Python チームの中国人プログラマーの「35 歳の呪い」に関係する人員削減を認めた 。Microsoft は 、 無力な中年者にとっては幸運なおもちゃでもある。強力で GPT-4.5 の疑いがある; Tongyi Qianwen オープンソース 8 モデルWindows 1.0 が 3 か月以内に正式に GA Windows 10 の市場シェアは 70% に達し、Windows 11 GitHub がAI ネイティブ開発ツール GitHub Copilot Workspace JAVAをリリースOLTP+OLAP を処理できる唯一の強力なクエリです。これが最高の ORM です。