트랜스포머의 "생각" 방법 알아보기

모바일 개발 2023-03-28 20:35:28 독서 시간: null

트랜스포머 모델은 AI 시스템의 기초입니다. "Transformer 작동 방식"의 핵심 구조에 대한 다이어그램은 이미 무수히 많습니다.

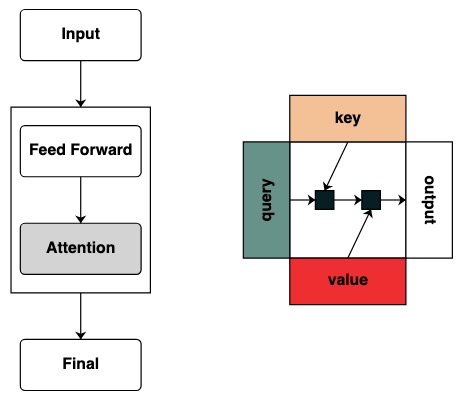
그러나 이러한 다이어그램은 이 모델을 계산하기 위한 프레임워크의 직관적인 표현을 제공하지 않습니다. 연구자가 Transformer의 작동 방식에 관심이 있을 때 작동 방식에 대한 직관을 갖는 것이 매우 유용합니다.

Thinking Like Transformers 논문에서는 Transformer 계산을 직접 계산하고 모방하는 Transformer 클래스의 컴퓨팅 프레임워크를 제안합니다. RASP 프로그래밍 언어를 사용하여 각 프로그램은 특별한 Transformer로 컴파일됩니다.

이 블로그 게시물에서는 Python에서 RASP(RASPy)의 변형을 재현했습니다. 언어는 원본과 거의 동일하지만 흥미로운 몇 가지 변경 사항이 더 있습니다. 이러한 언어를 사용하여 저자 Gail Weiss의 작업은 작동 방식을 이해하는 데 도움이 되는 흥미롭고 올바른 방법을 제공합니다.

!pip install git+https://github.com/srush/RASPy

언어 자체에 대해 이야기하기 전에 Transformers를 사용한 코딩의 예를 살펴보겠습니다. 다음은 뒤집기를 계산하는 코드입니다. 즉, 입력 시퀀스를 뒤집습니다. 코드 자체는 이 결과에 도달하기 위해 주의 및 수학적 계산을 적용하기 위해 두 개의 Transformer 레이어를 사용합니다.

def flip():
    length = (key(1) == query(1)).value(1)
    flip = (key(length - indices - 1) == query(indices)).value(tokens)
    return flip
flip()

기사 디렉토리

  • 파트 1: 코드로서의 트랜스포머
  • 2부: 트랜스포머로 프로그램 작성하기

코드로서의 트랜스포머

우리의 목표는 트랜스포머 표현을 최소화하는 일련의 계산 형식을 정의하는 것입니다. 트랜스포머의 각 언어 구조와 그에 상응하는 언어 구조를 유추하여 설명합니다. (공식 언어 사양은 이 문서 하단의 논문 전문 링크를 참조하십시오.)

언어의 핵심 단위는 하나의 시퀀스를 같은 길이의 다른 시퀀스로 변환하는 시퀀스 작업입니다. 나중에 변형이라고 부르겠습니다.

입력하다

Transformer에서 기본 레이어는 모델에 대한 피드포워드 입력입니다. 이 입력에는 일반적으로 원시 토큰 및 위치 정보가 포함됩니다.

코드에서 토큰의 기능은 모델 다음에 토큰을 반환하는 가장 간단한 변환을 나타내며 기본 입력 시퀀스는 "hello"입니다.

tokens

변환에서 입력을 변경하려면 입력 방법을 사용하여 값을 전달합니다.

tokens.input([5, 2, 4, 5, 2, 2])

트랜스포머로서 우리는 이러한 시퀀스의 위치를 ​​직접 받아들일 수 없습니다. 그러나 위치 임베딩을 시뮬레이션하기 위해 위치 인덱스를 얻을 수 있습니다.

indices


sop = indices
sop.input("goodbye")

피드포워드 네트워크

입력 계층을 통과한 후 피드포워드 네트워크 계층에 도달합니다. Transformer에서 이 단계는 수학적 연산을 시퀀스의 각 요소에 독립적으로 적용합니다.

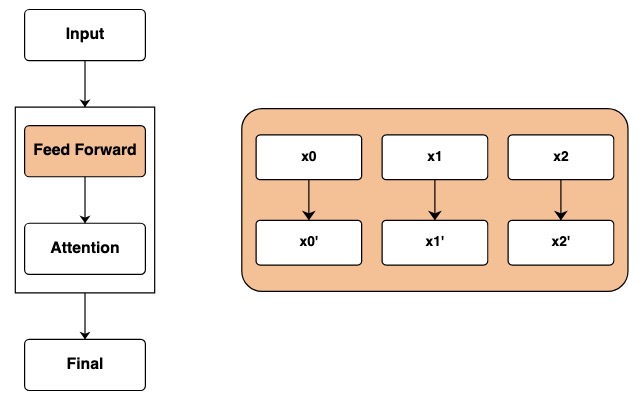
코드에서 변환을 계산하여 이 단계를 나타냅니다. 시퀀스의 각 요소에 대해 독립적인 수학 연산이 수행됩니다.

tokens == "l"

결과는 새 입력이 재구성되면 리팩터링된 것으로 계산되는 새 변환입니다.

model = tokens * 2 - 1
model.input([1, 2, 3, 5, 2])

이 작업은 여러 변환을 결합할 수 있습니다. 예를 들어 위에서 언급한 토큰과 인덱스를 예로 들어 Transformer를 클래스화하여 여러 정보를 추적할 수 있습니다.

model = tokens - 5 + indices
model.input([1, 2, 3, 5, 2])


(tokens == "l") | (indices == 1)

우리는 예를 들어 where유사한 if기능을 변환을 더 쉽게 작성할 수 있도록 몇 가지 도우미 기능을 제공합니다.

where((tokens == "h") | (tokens == "l"), tokens, "q")

mapint문자열 을 . (사용할 수 있는 단순 신경망으로 계산된 연산에 사용자는 주의해야 함)

atoi = tokens.map(lambda x: ord(x) - ord('0'))
atoi.input("31234")

함수(함수)는 이러한 변환의 캐스케이드를 쉽게 설명할 수 있습니다. 예를 들어 와 atoi를 적용하고 2를 더한 연산은 다음과 같다.

def atoi(seq=tokens):
    return seq.map(lambda x: ord(x) - ord('0')) 

op = (atoi(where(tokens == "-", "0", tokens)) + 2)
op.input("02-13")

주의 필터

주의 메커니즘을 적용하기 시작하면 상황이 흥미로워지기 시작합니다. 이렇게 하면 시퀀스의 서로 다른 요소 간에 정보를 교환할 수 있습니다.

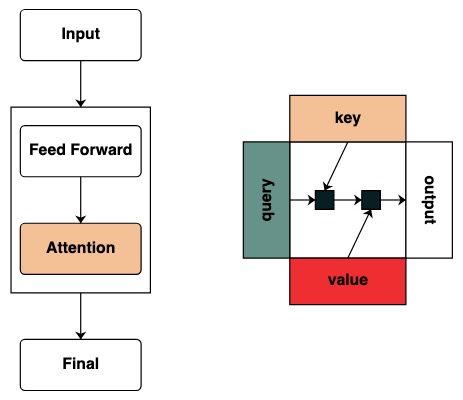
키와 쿼리의 개념을 정의하기 시작합니다. 키와 쿼리는 위의 변환에서 직접 생성할 수 있습니다. 예를 들어 키를 정의하려는 경우 키라고 합니다 key.

key(tokens)

query같은

query(tokens)

스칼라는 또는 로 key사용할 query있으며 기본 시퀀스의 길이로 브로드캐스팅됩니다.

query(1)

키와 쿼리 간에 작업을 적용하는 필터를 만듭니다. 이는 각 쿼리와 관련된 키를 나타내는 이진 행렬에 해당합니다. 트랜스포머와 달리 이 어텐션 매트릭스에는 가중치가 추가되지 않습니다.

eq = (key(tokens) == query(tokens))
eq

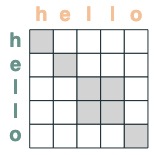
몇 가지 예:

  • 선택기의 일치 위치는 1만큼 오프셋됩니다.
offset = (key(indices) == query(indices - 1))
offset

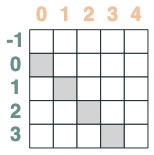
  • 키가 쿼리보다 이전인 선택기:
before = key(indices) < query(indices)
before

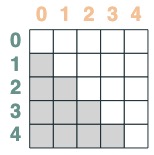
  • 키가 쿼리보다 늦은 선택기:
after = key(indices) > query(indices)
after

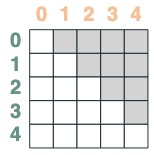
선택기는 부울 연산을 통해 결합할 수 있습니다. 예를 들어, 이 선택자는 before와 eq를 결합하고 행렬에 키와 값 쌍을 포함하여 이를 표시합니다.

before & eq

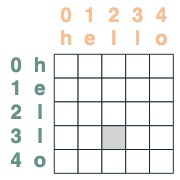
주의 메커니즘 사용

어텐션 셀렉터가 주어지면 집계를 위한 일련의 값을 제공할 수 있습니다. 해당 선택자가 선택한 진리값을 누적하여 집계합니다.

(참고: 원래 논문에서는 평균 집계 연산을 사용하고 평균 집계가 합계 계산을 나타낼 수 있는 영리한 구조를 보여줍니다. RASPy는 단순하게 유지하고 조각화를 피하기 위해 기본적으로 누적을 사용합니다. 필요한 레이어 수를 과소 평가할 수 있습니다. 평균 기반 모델은 이 레이어 수의 두 배가 필요할 수 있습니다.)

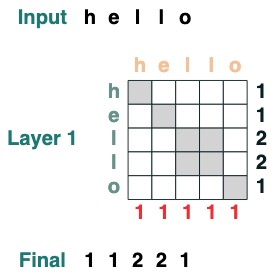
집계 작업을 통해 히스토그램과 같은 기능을 계산할 수 있습니다.

(key(tokens) == query(tokens)).value(1)

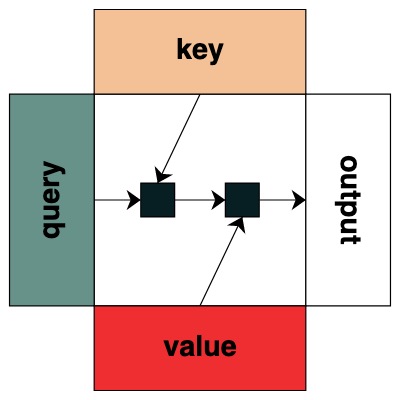
시각적으로 우리는 왼쪽에 쿼리, 상단에 키, 하단에 값, 오른쪽에 출력이 있는 그래프 구조를 따릅니다.

일부 주의 메커니즘 작업에는 입력 토큰이 필요하지 않습니다. 예를 들어 시퀀스 길이를 계산하기 위해 "모두 선택" 어텐션 필터를 만들고 값을 할당합니다.

length = (key(1) == query(1)).value(1)
length = length.name("length")
length

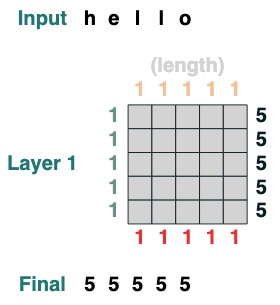
아래에 단계별로 표시된 더 복잡한 예가 있습니다. (인터뷰하는거랑 비슷함)

시퀀스의 인접한 값의 합을 계산하고 싶습니다. 먼저 앞으로 자릅니다.

WINDOW=3
s1 = (key(indices) >= query(indices - WINDOW + 1))  
s1

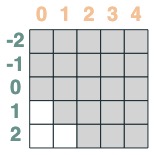
그런 다음 뒤로 자릅니다.

s2 = (key(indices) <= query(indices))
s2

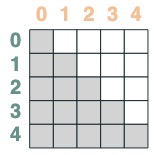
둘 다 교차:

sel = s1 & s2
sel

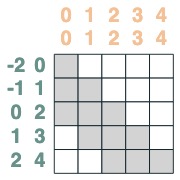
최종 집계:

sum2 = sel.value(tokens) 
sum2.input([1,3,2,2,2])

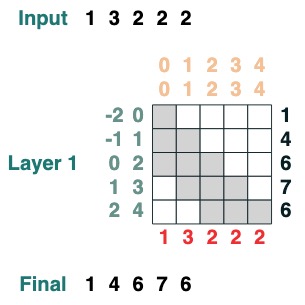
다음은 누적 합계를 계산할 수 있는 예이며 디버그에 도움이 되도록 변환 이름을 지정하는 기능을 소개합니다.

def cumsum(seq=tokens):
    x = (before | (key(indices) == query(indices))).value(seq)
    return x.name("cumsum")
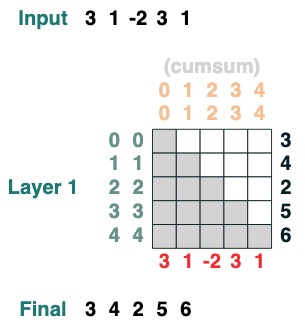
cumsum().input([3, 1, -2, 3, 1])

층

이 언어는 더 복잡한 변환 컴파일을 지원합니다. 또한 각 작업을 추적하여 레이어를 계산합니다.

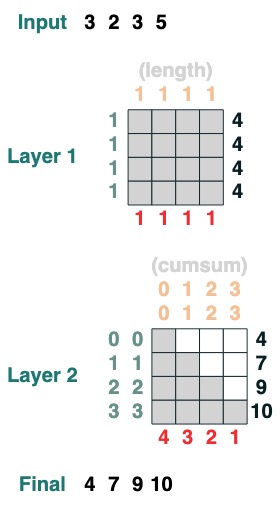
다음은 2계층 변환의 예입니다. 첫 번째 변환은 길이 계산에 해당하고 두 번째 변환은 누적 합계에 해당합니다.

x = cumsum(length - indices)
x.input([3, 2, 3, 5])

변환기를 사용한 프로그래밍

이 라이브러리를 사용하여 복잡한 작업을 작성할 수 있습니다.Gail Weiss는 이 단계를 분석하기 위해 나에게 매우 어려운 질문을 했습니다.

예: 문자열 "19492+23919"가 주어지면 올바른 출력을 로드할 수 있습니까?

직접 사용해 보고 싶다면 직접 사용해 볼 수 있는 버전을 제공합니다.

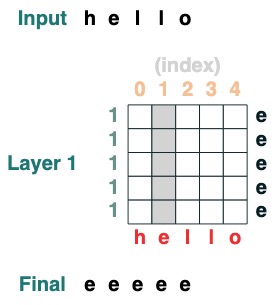
과제 1: 주어진 인덱스 선택

인덱스 i에

def index(i, seq=tokens):
    x = (key(indices) == query(i)).value(seq)
    return x.name("index")
index(1)

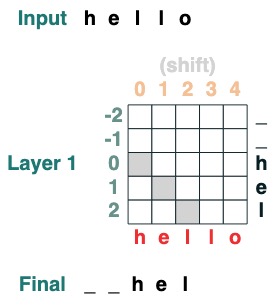
과제 2: 전환

i모든 토큰을 위치 만큼 오른쪽으로 이동합니다.

def shift(i=1, default="_", seq=tokens):
    x = (key(indices) == query(indices-i)).value(seq, default)
    return x.name("shift")
shift(2)

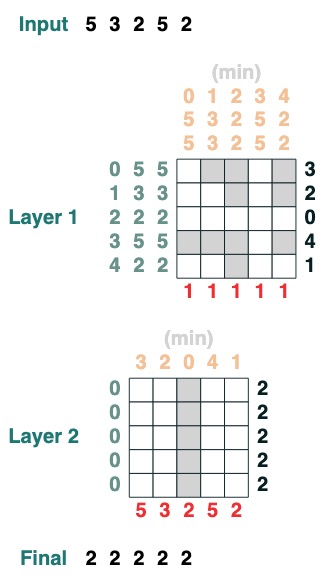
과제 3: 최소화

시퀀스의 최소값을 계산합니다. (이 단계는 어려워집니다. 우리 버전은 2계층 어텐션 메커니즘을 사용합니다.)

def minimum(seq=tokens):
    sel1 = before & (key(seq) == query(seq))
    sel2 = key(seq) < query(seq)
    less = (sel1 | sel2).value(1)
    x = (key(less) == query(0)).value(seq)
    return x.name("min")
minimum()([5,3,2,5,2])

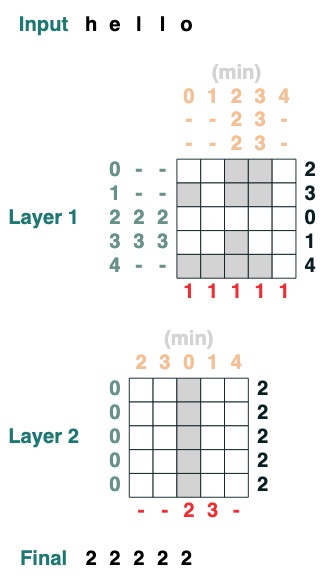
과제 4: 첫 번째 색인

토큰 q로 첫 번째 인덱스 계산(2개 레이어)

def first(q, seq=tokens):
    return minimum(where(seq == q, indices, 99))
first("l")

과제 5: 오른쪽 정렬

패딩 시퀀스를 오른쪽 정렬합니다. 예: " ralign().inputs('xyz___') ='—xyz'"(2개 레이어)

def ralign(default="-", sop=tokens):
    c = (key(sop) == query("_")).value(1)
    x = (key(indices + c) == query(indices)).value(sop, default)
    return x.name("ralign")
ralign()("xyz__")

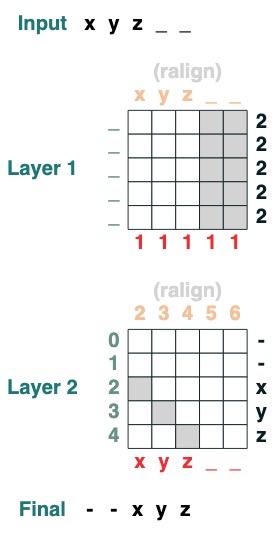
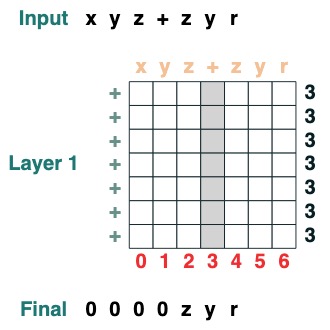
도전 6: 분리

시퀀스를 토큰 "v"에서 두 부분으로 나누고 오른쪽 정렬(2개 레이어):

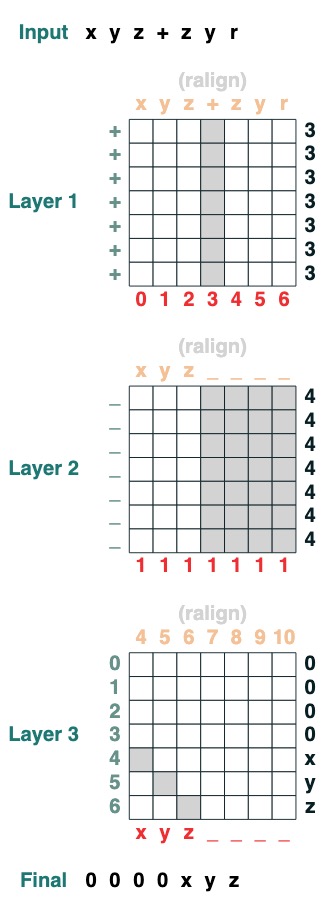
def split(v, i, sop=tokens):

    mid = (key(sop) == query(v)).value(indices)
    if i == 0:
        x = ralign("0", where(indices < mid, sop, "_"))
        return x
    else:
        x = where(indices > mid, sop, "0")
        return x
split("+", 1)("xyz+zyr")


split("+", 0)("xyz+zyr")

일곱 번째 과제: 스와이프

특수 토큰 "<"을 가장 가까운 "<" 값(2단계)으로 바꿉니다.

def slide(match, seq=tokens):
    x = cumsum(match) 
    y = ((key(x) == query(x + 1)) & (key(match) == query(True))).value(seq)
    seq =  where(match, seq, y)
    return seq.name("slide")
slide(tokens != "<").input("xxxh<<<l")

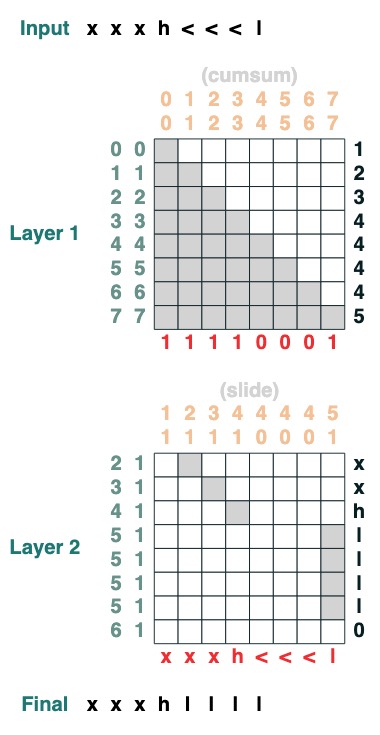
여덟 번째 과제: 증가

두 숫자의 덧셈을 수행하려고 합니다. 단계는 다음과 같습니다.

add().input("683+345")
  1. 두 부분으로 나눕니다. 플라스틱으로 전환합니다. 가입하다

"683+345" => [0, 0, 0, 9, 12, 8]

  1. carry 절을 계산합니다. 3가지 가능성: 1 캐리, 0 캐리 안함, < 아마도 캐리.

[0, 0, 0, 9, 12, 8] => "00<100"

  1. 슬라이딩 캐리 계수

"00<100" => 001100"

  1. 완전한 추가

이들은 1줄의 코드입니다. 전체 시스템은 6개의 주의 메커니즘입니다. (하지만 Gail은 충분히 주의하면 5분 안에 할 수 있다고 합니다!).

def add(sop=tokens):
    # 0) Parse and add
    x = atoi(split("+", 0, sop)) + atoi(split("+", 1, sop))
    # 1) Check for carries 
    carry = shift(-1, "0", where(x > 9, "1", where(x == 9, "<", "0")))
    # 2) In parallel, slide carries to their column                                         
    carries = atoi(slide(carry != "<", carry))
    # 3) Add in carries.                                                                                  
    return (x + carries) % 10
add()("683+345")


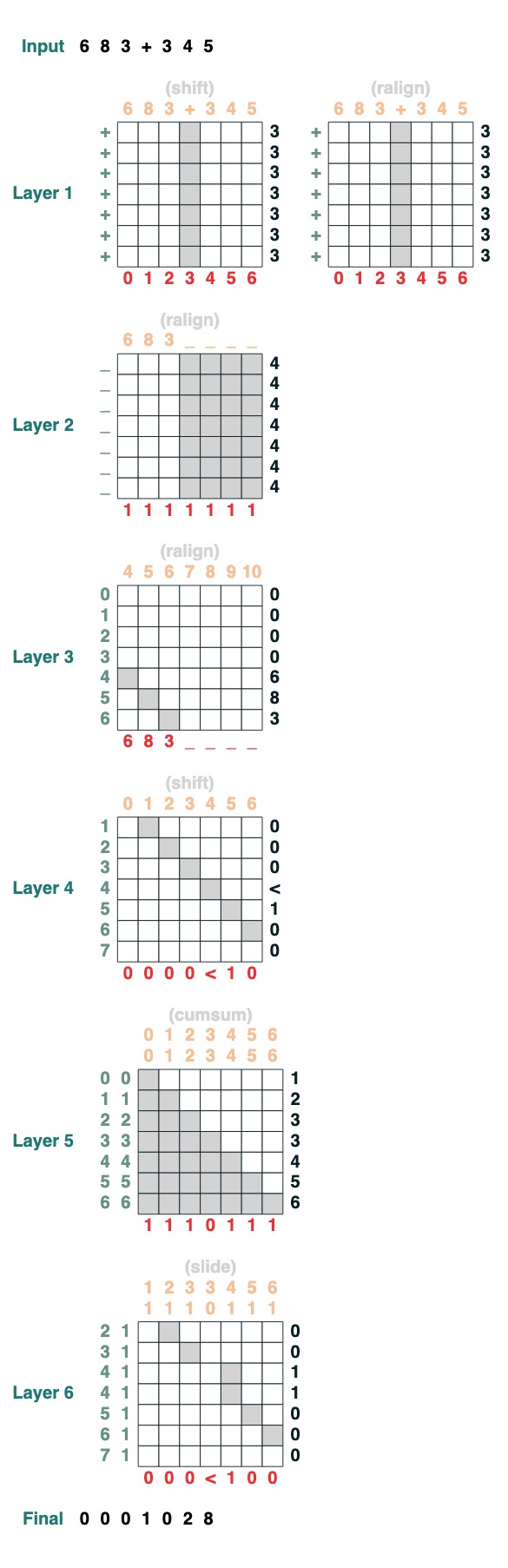
683 + 345

1028

완벽하게 완료!

참조 및 텍스트 내 링크:

<시간>

영어 원문: Thinking Like Transformers

역자: innovation64(Li Yang)

{{o.이름}}
{{이름}}

추천

출처my.oschina.net/HuggingFace/blog/7564937
추천
행
자바 얼굴 질문 2020년 1월 14일 설정
Elasticsearch-6.7.0 시리즈 (여섯) 클러스터 암호를 설정 ES
오늘, 수확 포인트 2019년 9월 5일
「解析」Jetson 安装 Jtop
공원을 블로그에 블로그 만들기
1070 Mooncake (25 분)
내 첫 조각 개발자 버전
[파이썬] 파이썬 파일을 EXE 실행 파일에 패키지되어
어떻게 당신의 어머니 게시판에 블로그를 추가하는 방법을 가르쳐
동영상 제작의 모든 고민, 이 동영상 계정 다운로드 도구를 사용하세요!
아카이브
기타
2020-04-08(1460)
2020-04-07(1517)
2020-04-06(1499)
2020-04-05(1440)
2020-04-04(1629)
2020-04-03(1644)
2020-04-02(1572)
2020-04-01(1665)
2020-03-31(1639)
2020-03-30(1334)

코드 세계

© 2018 codetd.com