Алгоритм выборки MCMC и т.д.

Оригинальная ссылка: http://www.cnblogs.com/CSLaker/p/9962912.html

Во-первых, прямой выборки

Мы думали , что прямая выборка равномерно распределяется по образцу, реализовать выборку случайным образом распределены. Потому что хорошее предположение равномерно распределены выборки, распределение выборки мы хотим плохой выбор, он бы некоторые сложные стратегии выборки , принятой простой запрос.
Y предполагается подчиняться распределение р (у), который является кумулятивная функция распределения ВПР ч (у), с образцом г ~ Uniform (0,1), мы Пусть Z = Н (Y), т.е., Y = H (Z) ^ (-1), у является результатом выборки распределения Р (у).

314331-a158633099c6fd5c-2

ВПР и обратное преобразование и применение основной идеи прямой выборки. В оригинальной распределения р (у), если большая область распространения [а, Ь], то соответствующая кривая в КОР, [ч (а), ч (б)] наклона кривой будет больше. Затем, после того, как обратное преобразование, когда ось у (г) равномерно распределена сэмпл, мульти-часть профиля (ось у части занимающих поли) соответствующая вероятность образец, полученный еще больше,

ограничение

На практике, распределение всех образцов являются более сложными, и решение разрешающие CDF обратной функции не представляется возможным.

Во-вторых, отказаться от выборки

Образцы отвергаются легким распределением выборки исходного алгоритма выборки генерирует общее распределение образца оно трудно непосредственно образец. Так как р (х) не может быть слишком сложным прямой выборки в программе, то это может быть распределение выборки д (х), например, гауссовым распределением, а также способ в соответствии с определенным отвергают некоторые из образцов, для достижения объекта близкого р (х) распределения.

25225434-fd6db018b45d4152a09ea1de2b5304ad

шаги расчета

Установка удобно дискретизации функцию д (х), а константа к, такое, что р (х) ниже общего к * д (х) в. (Смотри выше)

ось х: от Q (х), полученного путем отбора проб распределения;
Направление оси у: от равномерного распределения (0, к * д (а)), полученный путем отбора проб U;
Если он упал прямо в серой области: и> р (а), отказался принять это или отбор проб;
Повторите этот процесс.

шаг расчета (БН)

Априорное распределение вероятностей сеть, указанная генерировать выборочные образцы;
Отклонить все доказательства не соответствует образцу;
В остальных образцах уровня падающих Х = х частые отсчеты для получения расчетной вероятности,

ограничение

Отклоненные слишком много образцов! В качестве доказательства увеличения числа переменных данные согласуются с долей образца е, занимаемых во всех образцах снизились в геометрической прогрессии, так что проблема с этим подходом является комплексом полностью недоступна.
Трудно найти подходящий к * д (а), чтобы принять вероятность может быть низкой.

В-третьих, выборки по значимости (вероятность того, взвешивание)

правдоподобие Весоизмерительное

выборки Важность используется в основном для поиска сложного распределения р (х) среднего , последний не получил образцы.

Простая идея распределения выборки значения Q (X) с помощью простой дискретизации этого простого распределения д (х) Полученные образцов всех. Но это, конечно, не соответствует результирующее распределение выборки р (х), необходимо для каждого дополнительного образца соответствующего весового коэффициента важности. Значение выборки, чтобы р (х0) / д (х0) в качестве значения веса от веса каждого образца. Таким образом, когда образец и распределение р (х) похож на соответствующий вес больше, когда распределение р (х) большая разница, соответствующие весовые коэффициенты малы. Такой подход проба с весом образца важности права подчиняться распределению (г) Q, после того, как результаты веса, помноженного на образце на самом деле с учетом распределения р (г).

314331-0096a433b005eb92-2

Благодаря приведенной выше формулы, мы можем знать значение выборки можно использовать для аппроксимации среднего сложного распределения.

В-четвертых, выборка Гиббса

Рассмотрим пример: E: есть, учиться, играть, время Т: утром, днем, вечером, погода W: солнечно, ветрено, дождь. Образцы (Е, Т, W) отвечать определенное распределение вероятностей. Теперь мы хотим быть выбраны, например: игры + + солнечный день.

Проблема заключается в том, что мы не знаем р (Е, Т, W) , или которые не знают , совместное распределение трех вещей. Конечно, если известно, нет необходимости использовать пробник Гиббса. Тем не менее, мы знаем три вещи условные распределения. Другими словами, р (Е | T, W ), р (Т | Е, W), P (W | Е, Т). Для того, чтобы сделать теперь с помощью этих трех условий , известных распределения выборочного метода Гиббса , а затем получить совместное распределение.
Конкретные методы: Во- первых, сочетание случайной инициализации, то есть обучение + + ветреная ночь, а затем изменить их в соответствии с переменной условной вероятности. В частности, предположу , что мы знаем + ветреную ночь, мы даем E генерирует переменный, например, обучение → есть. Затем мы следуем условной вероятности изменения при переменной, в зависимости от обучения + ветер, ночь превратилась утром. Точно так же, ветер в ветер (конечно, может стать тем же переменным). Такое обучение + ужин + ночь + утром + → ветреные ветреная. Таким же образом , чтобы получить последовательность, каждый из которых содержит три переменные, то есть цепь Маркова. Затем пропустить определенное количество исходных клеток (такие , как 100) и блок сепаратора принимать определенное число (например , прокладку 20 , чтобы принять). Такой образец блока приближается совместное распределение.

25225719-116e5550e9fd448f894cddc6b6ab02b4

В-пятых, образец резервуара

Отбор пробы пласта (коллектор выборка), то есть, п может быть осуществлен как в данном О (п) время случайной вероятности, например: от 1000 средних вероятностных данных 100 экстрагированных. Кроме того, если сумма сбора данных, в частности, большой или растет (что эквивалентно общему количеству неизвестного набора данных), алгоритм может по-прежнему равна вероятности выборки.

шаги алгоритма:

Сначала выберите первые к элементам потока данных, хранящемуся в множестве А;
Из J (к + 1 <= у <= п) элементов каждый раз, когда он начинает сначала с вероятностью р = K / J Выберите осталось ли J-й элемент. Если выбран J, случайным образом выбирается из элемента А и заменяет его с элементом J, в противном случае, непосредственно из элемента;
Повторите шаг 2 до конца последнего множества А, чтобы гарантировать, что оставшиеся к элементам в случайном порядке.

Шесть, алгоритмы MCMC

Случайная выборка стохастического моделирования: Гиббс выборки Гиббса выборки

MCMC алгоритмы резюме обучения

[Акцент] метод отбора проб (б) MCMC алгоритмы введены и соответствующий код реализация

Теорема Маркова цепь сходимости

Цепь Марков теорема: Если непериодическая цепь Маркова , имеющая вероятность перехода матрица Р, и любые из двух состояний находятся в сообщении, то \ (\ lim_ {р \ к \ infty} P_ {Ij} ^ п \) присутствует и не зависит от I, обозначаемая \ (\ lim_ {P \ к \ infty} из P_ ^ {} Ij п- = \ PI (J) \) , мы имеем:

20180604161544272

В котором \ (\ р = [\ пи (1), \ пи (2), ..., \ р (к), ...], \ sum_ {г = 0} ^ {\ infty} \ pi_i = 1 \ р \) называется стационарным распределением цепей Маркова.

Все методы MCMC (цепи Маркова Монте-Карло) основаны на теореме в качестве теоретической основы.

Описание:

Состояние теоремы марковской цепи не требует ограниченно, может быть множество бесконечно;
Теорема «непериодическая» концепция не объясняет, потому что подавляющее большинство цепей Маркова мы сталкиваемся в апериодическом;

20180604161729263

Гладкие и подробные условия

012132441751392

012132476599223

Для нового распределения, как построить соответствующую матрицу перехода?

Для распределения \ (\ PI (X) \) , в соответствии с подробным стабильным состоянием , если конфигурация переноса матрицы Р удовлетворяет условию \ (\ ПИ (I) , из P_ {Ij из} = \ PI (J) от P_ {СО} \) , то \ (\ р (х) \ ) является стационарным распределением переходной цепи Маркова матрицы может быть построены в соответствии с этим условием.

Как правило, начальная матрица перехода \ (Р \) , как правило , не удовлетворяет стационарные условия подробно, мы строим матрицу перехода путем введения нового курса приема \ (P «\) , и так \ (\ р (х) \ ) , чтобы удовлетворить дотошное стабильное состояние. Таким образом, мы можем использовать любую вероятность перехода матрицу (равномерное распределение, гауссово распределение) в качестве вероятности перехода между состояниями.

Если предположить , что вероятности переходов между состояниями одинаковы, то алгоритм при получении скорости может просто использовать \ (\ Pi (J) / \ р (I) \) представлены.

выборки Метрополиса-Гастингс

Для распределения заданной вероятности р (х), мы надеемся иметь удобный способ получения его соответствующий образца. Так как цепь Маркова может сходиться к стационарному распределению, поэтому очень хорошая идея: если мы можем построить матрицу перехода для цепи Маркова Р так, что стационарное распределение цепи Маркова точно р (х), то из любое отклонение по начальной передаче состояния x0 цепи Маркова, чтобы получить последовательность x0, x1, x2, ⋯ х передач, х +-⋯ ,, если цепь Маркова сошлось на этапе п, так что мы получаем π (х) образцов хп, хп + 1 ⋯.

MCMC-что-то-1.jpg

В состоянии цепи Маркова, каждое состояние представляет собой образец \ (x_n \) , то есть назначение всех переменных.

Анализируя источник MCMC может быть известно: то же самое состояние вероятности перехода между гипотезами, то следующий образец на образце будет зависеть от образца. Предполагая , что исходное распределение вероятности , соответствующее образец \ (\ р (х) \ ) мало, скорость принятия высокой вероятности образца 1, с другой стороны, если распределение вероятностей исходного образца \ (\ р (х ) \) велико, то следующая большая вероятностная выборка будет отклонена. Этот механизм гарантирует , что полученный образец подлежит распределению \ (\ PI (Х-) \) .

Из приведенного выше анализа, распределение вероятностей , соответствующий образцу , если начальное состояние очень мало, то алгоритм в начале образцов , полученных в ходе операции (даже очень мало распределения вероятности выборки), весьма вероятно, будут получены, так что алгоритм отбор пробы начали работать образец не соответствует исходному распределению \ (\ PI (х-) \) . До тех пор , как алгоритм выборки с большой вероятностью распределения выборки ( этот случай является конвергенция! ), То после выборки образцов будут в основном подчиняться оригинальное распределение. Конечно, вы должны работать в течение определенного периода времени при прохождении из начального состояния распределения вероятностей для большого государства, этот процесс известен как процесс конвергенции. MCMC алгоритм после сходимости для того, чтобы распределение вероятностей \ (\ р (х) \ ) большое место , чтобы произвести большее количество образцов, то распределение вероятностей \ (\ р (х) \ ) небольшие местные производят меньше образцов.

Процесс переходного состояния марковского пройти многократное использование , чтобы достичь устойчивого состояния, на этот раз образец был относительно близко к реальному распределению. Этот процесс называется Ожог в . Может быть достигнуто в основном путем отбрасывания ожога в передней части образцов N результатов.

сомнение

MCMC конвергенция Что это значит? Этот процесс приводит к тому, что параметры будут обновлены конвергенции? Как определить, когда схождение?

Нет параметров процесса конвергенции будет обновляться конвергенция идей подобный закон больших чисел. Применение алгоритма MCMC выборки, первоначальный небольшого размера выборки, а также распределения может подвергнуть сложное распределение \ (\ р (х) \ ) отличается очень далеко, но так как количество переходов состояний (приложение матрица передачи P), основанным на доказательство теоремы, окончательное распределение выборки будет постепенно подчиняться комплексное распределение \ (\ PI (Х-) \) .
\ (\ Р \) является распределение вероятности каждого состояния ему соответствует? Если да, то изначально выбрал государство, \ (\ р \) Как установить? В MCMC или процесса сертификации, начальная \ (\ р \) распределения вероятностей , как настроить?

При доказательстве MCMC, \ (\ PI \) является распределение вероятности каждого состояния соответствует. Доказательство дано начальное \ (\ р \) следует, чтобы доказать , является ли исходный образец в соответствии с тем, что распределяется, после передачи определенного количества полученных образцов подлежат комплексной распределения \ (\ PI (х-) \) , в фактическое выполнение кода, без этого \ (\ пи \) устанавливается.

Семь, код

import numpy as np
import random
import matplotlib.pyplot as plt
import pandas as pdf

Отклонение выборки

def f(x):
    if 0 <= x and x <= 0.25:
        y = 8 * x
    elif 0.25 < x and x <= 1:
        y = (1 - x) * 8/3
    else:
        y = 0
    return y

def g(x):
    if 0 <= x and x <= 1:
        y = 1
    else:
        y = 0
    return y

def plot(fun):
    X = np.arange(0, 1.0, 0.01)
    Y = []
    for x in X:
        Y.append(fun(x))
    plt.plot(X, Y)
    plt.xlabel("x")
    plt.ylabel("y")
    plt.show()

plot(f)
plot(g)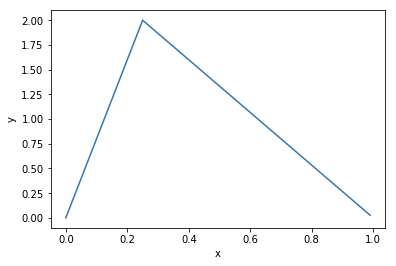

def rejection_sampling(N=10000):
    M = 3
    cnt = 0
    samples = {}

    while cnt < N:
        x = random.random()
        acc_rate = f(x) / (M * g(x))
        u = random.random()
        if acc_rate >= u:
            if samples.get(x) == None:
                samples[x] = 1
            else:
                samples[x] = samples[x] + 1
            cnt = cnt + 1
            
    return samples

s = rejection_sampling(100000)

X = []
Y = []
for k, v in s.items():
    X.append(k)
    Y.append(v)

plt.hist(X, bins=100, edgecolor='None')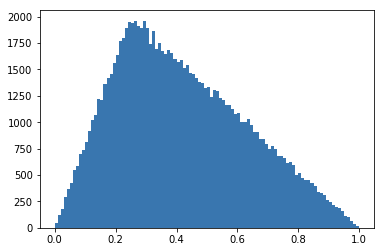

MCMC выборки

Метрополис-Гастингс алгоритм

Ссылка: MCMC алгоритмы , связанные с внедрением и реализацией коды

PI = 3.1415926

def get_p(x):
    # 模拟pi函数
    return 1/(2*PI)*np.exp(- x[0]**2 - x[1]**2)

def get_tilde_p(x):
    # 模拟不知道怎么计算Z的PI，20这个值对于外部采样算法来说是未知的，对外只暴露这个函数结果
    return get_p(x)

def domain_random(): #计算定义域一个随机值
    return np.random.random()*3.8-1.9

def metropolis(x):
    new_x = (domain_random(),domain_random()) #新状态
    #计算接收概率
    acc = min(1,get_tilde_p((new_x[0],new_x[1]))/get_tilde_p((x[0],x[1])))
    #使用一个随机数判断是否接受
    u = np.random.random()
    if u<acc:
        return new_x
    return x

def testMetropolis(counts = 100,drawPath = False):
    plt.figure()
    #主要逻辑
    x = (domain_random(),domain_random()) #x0
    xs = [x] #采样状态序列
    for i in range(counts):
        xs.append(x)
        x = metropolis(x) #采样并判断是否接受
    #在各个状态之间绘制跳转的线条帮助可视化
    X1 = [x[0] for x in xs]
    X2 = [x[1] for x in xs]
    if drawPath: 
        plt.plot(X1, X2, 'k-',linewidth=0.5)
    ##绘制采样的点
    plt.scatter(X1, X2, c = 'g',marker='.')
    plt.show()

testMetropolis(5000)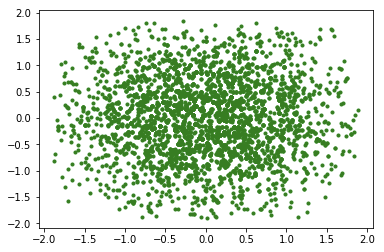

def metropolis(x):
    new_x = domain_random()
    #计算接收概率
    acc = min(1,f(new_x)/f(x))
    #使用一个随机数判断是否接受
    u = np.random.random()
    if u<acc:
        return new_x
    return x

def testMetropolis(counts = 100,drawPath = False):
    plt.figure()
    #主要逻辑
    x = domain_random()
    xs = [x] #采样状态序列
    for i in range(counts):
        xs.append(x)
        x = metropolis(x) #采样并判断是否接受
    #在各个状态之间绘制跳转的线条帮助可视化
    plt.hist(xs, bins=100, edgecolor='None')  
#     plt.plot(xs)
    plt.show()

testMetropolis(100000)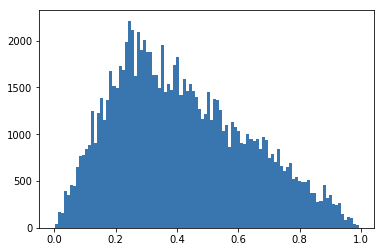

Гиббс выборки

def partialSampler(x,dim):
    xes = []
    for t in range(10): #随机选择10个点
        xes.append(domain_random())
    tilde_ps = []
    for t in range(10): #计算这10个点的未归一化的概率密度值
        tmpx = x[:]
        tmpx[dim] = xes[t]
        tilde_ps.append(get_tilde_p(tmpx))
    #在这10个点上进行归一化操作，然后按照概率进行选择。
    norm_tilde_ps = np.asarray(tilde_ps)/sum(tilde_ps)
    u = np.random.random()
    sums = 0.0
    for t in range(10):
        sums += norm_tilde_ps[t]
        if sums>=u:
            return xes[t]

def gibbs(x):
    rst = np.asarray(x)[:]
    path = [(x[0],x[1])]
    for dim in range(2): #维度轮询，这里加入随机也是可以的。
        new_value = partialSampler(rst,dim)
        rst[dim] = new_value
        path.append([rst[0],rst[1]])
    #这里最终只画出一轮轮询之后的点，但会把路径都画出来
    return rst,path

def testGibbs(counts = 100,drawPath = False):
    plt.figure()

    x = (domain_random(),domain_random())
    xs = [x]
    paths = [x]
    for i in range(counts):
        xs.append([x[0],x[1]])
        x,path = gibbs(x)
        paths.extend(path) #存储路径
        
    p1 = [x[0] for x in paths]
    p2 = [x[1] for x in paths]
    xs1 = [x[0] for x in xs]
    xs2 = [x[1] for x in xs]
    if drawPath: 
        plt.plot(p1, p2, 'k-',linewidth=0.5)
    ##绘制采样的点
    plt.scatter(xs1, xs2, c = 'g',marker='.')
    plt.show()

testGibbs(5000)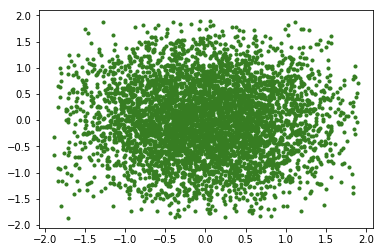

Воспроизводится в: https: //www.cnblogs.com/CSLaker/p/9962912.html