信号与系统(Python) 学习笔记 (8.1) 离散系统z域分析 -- 系统函数 H(z)

• 【总目录】
  • (1) 简介 Intro
  • (2) 傅里叶 Fourier
    • 常用函数的傅里叶变换汇总
  • (3) LTI 系统 与 滤波器
    • 二次抑制载波振幅调制接收系统 Python
  • (4) 取样 Sampling
  • (5) 离散傅里叶 Discrete Fourier
  • (6) 拉普拉斯变换 Laplace Transform
  • (7) 电路与系统函数
    • 连续系统
  • (8) 离散系统z域分析 – z变换
    • 系统函数 H(z)
      

---

8.2. 系统函数 H(z)

8.2.1. 系统函数 H(z) 定义

• 定义：

$F(z) \to \boxed{\underset{x=0}{H(z)}} \to Y_f(z)$

$H(z) = \frac{Y_{zs}(z)}{F(z)}$

• 物理含义:

$h(k) \leftrightarrow H(z) = \sum^{\infty}_{k=0} h(k) z^{-k}$
$H(z) = \mathcal{Z}[h(k)]$

• 计算方法:

  1. $H(z) = \frac{Y_{zs}(z)}{F(z)}$
  2. $H(z) = \mathcal{Z}[h(k)]$
  3. 由系统差分方程求 $H(z)$

• 应用:

  1. 求 $y_{zs}(k) = \mathcal{Z}[Y_{zs}(z)],\; Y_{zs}(z)= H(z)F(z)$ ;
  2. 求 $h(z)= \mathcal{Z}^{-1}[H(z)]$ ;
  3. 求 $f(k) = \mathcal{Z}^{-1}[F(z)], \; F(z) = \frac{Y_{zs}(z)}{H(z)}$ ;
  4. 表示系统特性：频率特性、稳定性等。

• 分解:

$f({\color{red}k}) = \frac{1}{2\pi j} \oint_c \frac{F(z)}{z} z^{ {\color{red}k}} dz, \; -\infty < k < \infty$

• 基本信号 $z^k$ :

$z_0^k \to \boxed{h(k)} \to z_0^k \cdot H(z_0)$

$f(k) \to \boxed{h(k)} \to y_f(k)$

• 任意信号:

$\frac{1}{2\pi j} \frac{F(z)}{z}\cdot z^k \to \frac{1}{2\pi j} \frac{F(z)}{z} \cdot z^k H(z)$
$\oint_c\frac{1}{2\pi j} \frac{F(z)}{z}\cdot z^k dz \to \oint_c\frac{1}{2\pi j} \frac{F(z)}{z} \cdot z^k H(z) dz$
$\oint_c\frac{1}{2\pi j} \frac{F(z)}{z}\cdot z^k dz \to \oint_c\frac{1}{2\pi j} \frac{ {\color{blue}F(z)\cdot H(z)} }{z} \cdot z^k dz$
$Y_f(z) = F(z) \cdot H(z)$

• 回顾 转换成时域
  $f(k)\star h(k) \leftrightarrow F(z) \cdot H(z)$

8.2.2. 系统特性

离散系统的零点与极点

• 类比

$\begin{aligned}H(z) & = \displaystyle \frac{B(z)}{A(z)}\\ & = \displaystyle \frac{b_m z^m + b_{m-1}z^{m-1} + \cdots + b_1 z + b_0}{z^n + a_{n-1}z^{n-1} + \cdots +a_1z+a_0}\\ & = \frac{b_m(z-\zeta_1)(z-\zeta_2)\cdots(z-\zeta_m)}{(z-P_1)(z-P_2)\cdots(z-P_n)} \\ &= \frac{b_m \prod^{m}_{j=1}(z-\zeta_j)}{\prod^{n}_{i=1}(z-P_i)}, \; m\leq n \end{aligned}$

• $H(z)$ 的零点:

$\zeta_i, \; i =1,2,\cdots, m$

• $H(z)$ 的极点:

$P_i, \; i =1,2,\cdots, m$

• 零/极点的种类：
  • 实数、
  • 复数 (复数零、极点必共轭 )
  • 一阶、二阶及二阶以上极点

零、极点与h(k)的关系

• 极点在单位圆内

  • 在实轴上:

    1. 一阶极点:
       $\frac{Az}{z-a}\leftrightarrow A {\color{blue}a^k\downarrow} \varepsilon(k),\; \lvert a \rvert <1$
    2. 二阶极点:
       $\frac{Az}{(z-a)^2}\leftrightarrow A{\color{blue}ka^{k-1}\downarrow} \varepsilon(k),\; \lvert a \rvert <1$

  • 不在实轴上:

    1. 一阶极点:
       $\frac{Az}{z-r e^{j\beta}} + \frac{A^*z}{z-re^{-j\beta}}\leftrightarrow 2\lvert A \rvert {\color{blue}r^k\downarrow} \cos(\beta k + \theta) \varepsilon(k),\; r<1$
    2. 二阶极点:
       $\frac{Az}{(z-r e^{j\beta})^2} + \frac{A^*z}{(z-re^{-j\beta})^2}\leftrightarrow 2\lvert A \rvert {\color{blue}r^{k-1}\downarrow} \cos(\beta (k-1) + \theta) \varepsilon(k),\; r<1$

  • 结论: 对应 $h(k)$按指数规律衰减；

• 极点在单位圆上

  • 在实轴上:

    1. 一阶极点:
       $\frac{Az}{z\pm 1}\leftrightarrow A {\color{blue}(\pm 1^k)} \varepsilon(k)$
    2. 二阶极点:
       $\frac{Az}{(z\pm 1)^2}\leftrightarrow A {\color{red}k\uparrow}{\color{blue}(\pm 1^{k-1})} \varepsilon(k)$

  • 不在实轴上:

    1. 一阶极点:
       $\frac{Az}{z-r e^{j\beta}} + \frac{A^*z}{z-re^{-j\beta}}\leftrightarrow 2\lvert A \rvert \cos(\beta k + \theta) \varepsilon(k),\; r<1$
    2. 二阶极点:
       $\frac{Az}{(z-r e^{j\beta})^2} + \frac{A^*z}{(z-re^{-j\beta})^2}\leftrightarrow 2\lvert A \rvert {\color{red}k\uparrow} \cos(\beta (k-1) + \theta) \varepsilon(k),\; r<1$

  • 结论: 一阶极点对应 $h(k)$为稳态分量；二阶及二阶以上极点对应 $h(k)$增长。

• 极点在单位圆外

  • 在实轴上:

    1. 一阶极点:
       $\frac{Az}{z-a}\leftrightarrow A {\color{blue}a^k\uparrow} \varepsilon(k),\; \lvert a \rvert >1$
    2. 二阶极点:
       $\frac{Az}{(z-a)^2}\leftrightarrow A{\color{blue}ka^k\uparrow} \varepsilon(k),\; \lvert a \rvert >1$

  • 不在实轴上:

    1. 一阶极点:
       $\frac{Az}{z-r e^{j\beta}} + \frac{A^*z}{z-re^{-j\beta}}\leftrightarrow 2\lvert A \rvert {\color{blue}r^k\uparrow} \cos(\beta k + \theta) \varepsilon(k),\; r>1$
    2. 二阶极点:
       $\frac{Az}{(z-r e^{j\beta})^2} + \frac{A^*z}{(z-re^{-j\beta})^2}\leftrightarrow 2\lvert A \rvert {\color{blue}r^{k-1}\uparrow} \cos(\beta (k-1) + \theta) \varepsilon(k),\; r>1$

  • 结论: 对应 $h(k)$按指数规律增长。

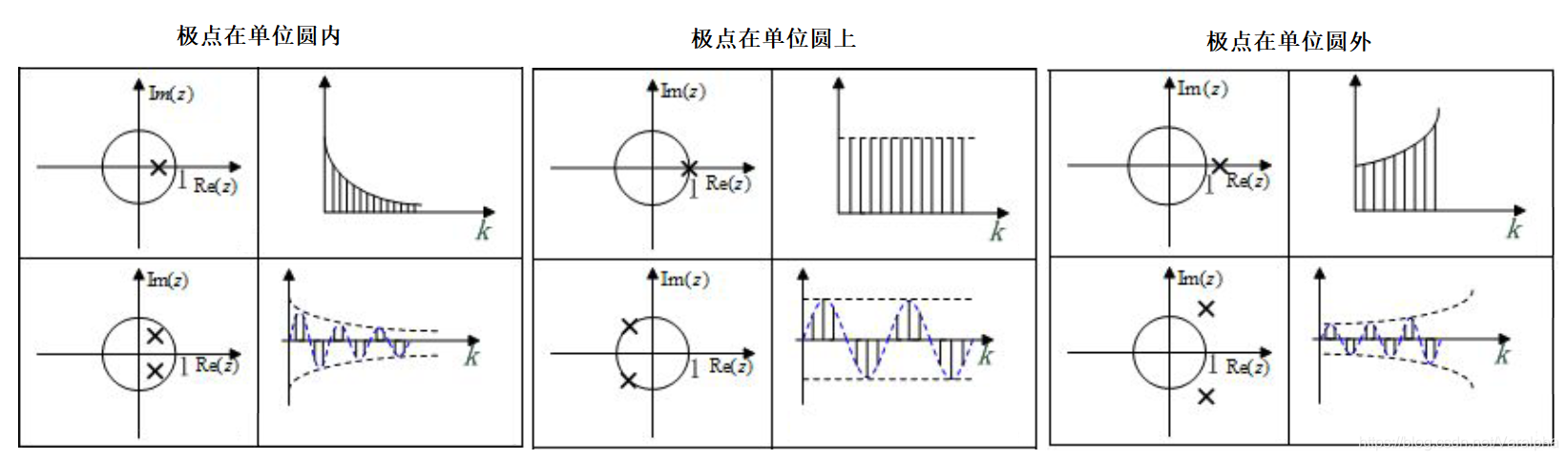
8.2.3. 离散系统稳定性判据（因果系统）

• 离散系统稳定的时域充要条件:(绝对可和)

$\sum^{\infty}_{k=-\infty} \lvert h(k)\rvert < \infty$

• 离散系统稳定性的Z域充要条件:

  • 若LTI离散系统的系统函数 $H(z)$ 的收敛域包含单位圆，则系统为稳定系统。
  • 若LTI离散因果系统稳定，要求其系统函数 $H(z)$ 的极点全部在单位圆内。
  • $\lvert p_j \rvert <1$

• 离散因果系统稳定性判定－－朱里准则（Jury stability criterion）
  $\begin{aligned}H(z) = \displaystyle \frac{B(z)}{A(z)} = \displaystyle \frac{b_m z^m + b_{m-1}z^{m-1} + \cdots + b_1 z + b_0}{a_nz^n + a_{n-1}z^{n-1} + \cdots +a_1z+a_0}\end{aligned}$
  

  • 要判断 $A(z)=0$ 的所有根的绝对值是否都小于 $1$ 。

  • 朱里准则指出: $A(z)=0$ 的所有根都在单位圆内的充要条件是:

    1. $A(1)>0$
    2. $(-1)^nA(-1)>0$
    3. $a_n>\lvert a_0\rvert \; c_{n-1}>\lvert c_0 \rvert \cdots r_2>\lvert r_0\rvert$
       对奇数行，其第1个元素必大于最后一个元素的绝对值。
    • 特例: 对二阶系统:
      $A(z) = a_2z^2 + a_1z + a_0$
      易得 $A(1)>0, \; A(-1),\; a_2>\vert a_0\vert$

8.2.4. 系统的方框图

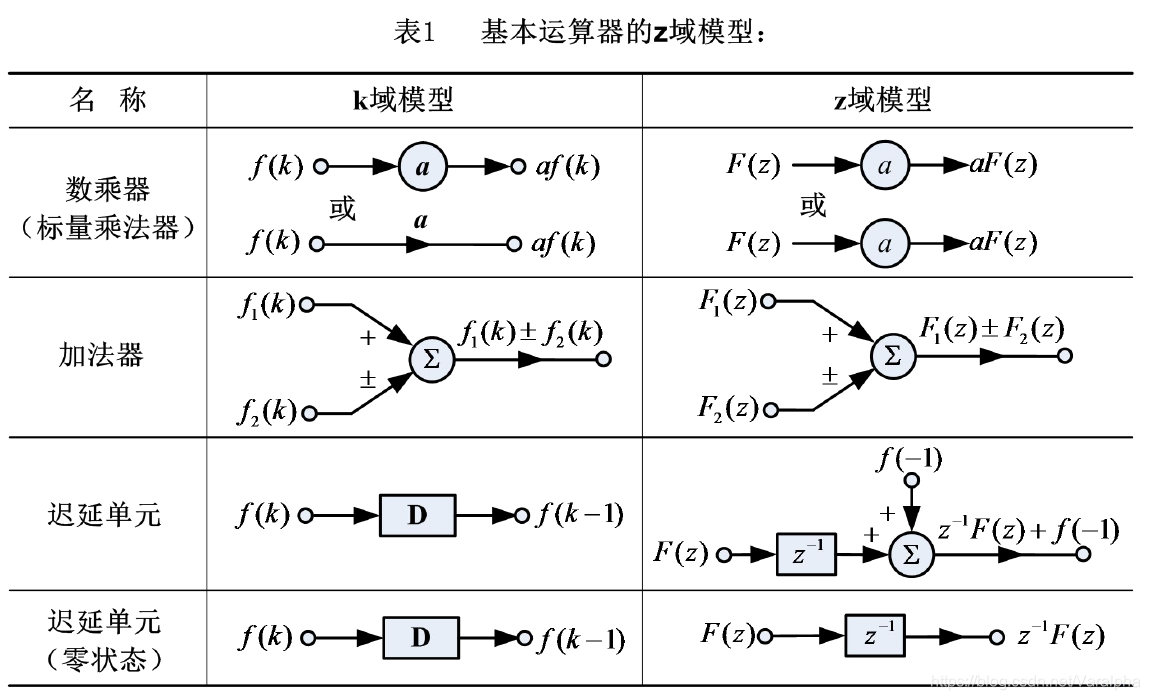
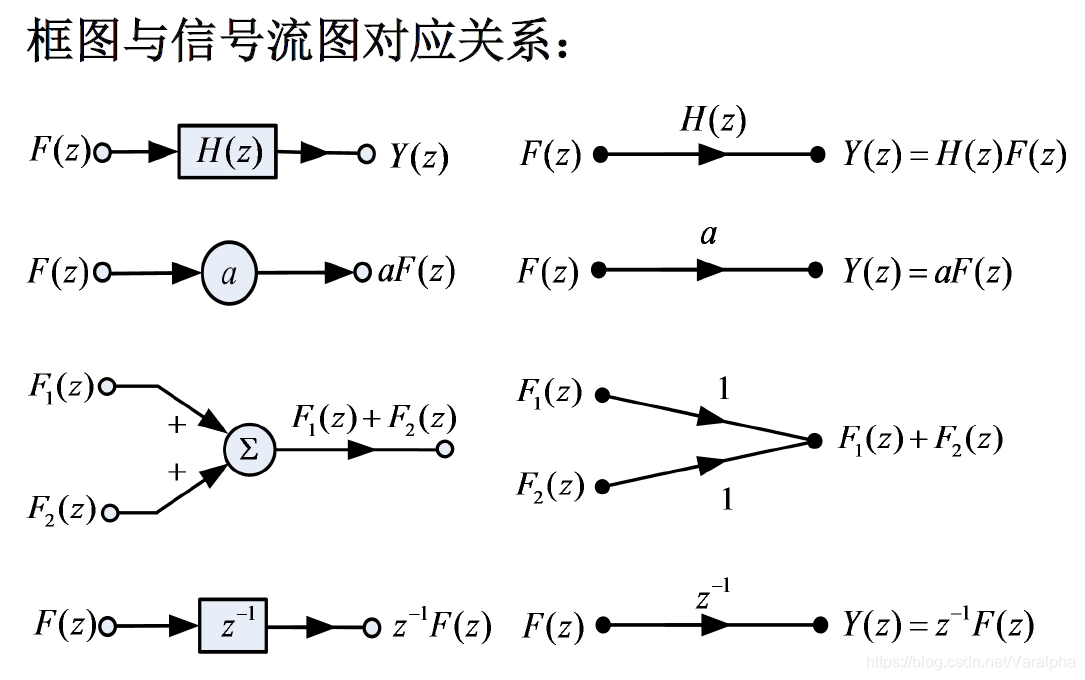
8.2.5. 系统的流图

• 系统流图

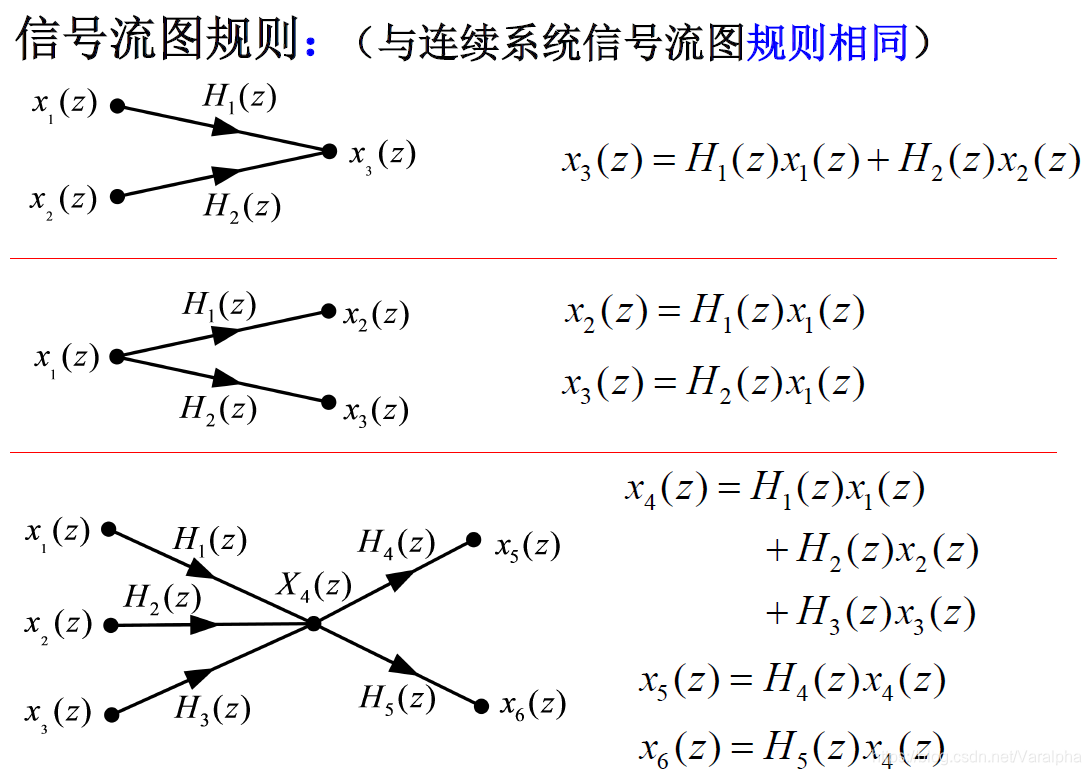
To TOP 至目录