Task4

条件随机场

马尔可夫过程

定义

假设一个随机过程中， $t_n$ 时刻的状态 $x_n$的条件发布，只与其前一状态 $x_{n-1}$ 相关，即：

$P(x_n|x_1,x_2,...,x_{n-1}) = P(x_n|x_{n-1})$

则将其称为 马尔可夫过程。

隐马尔科夫算法

定义

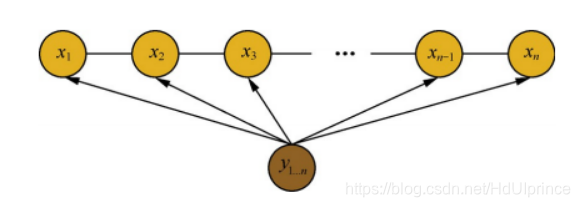
隐马尔科夫算法是对含有未知参数（隐状态）的马尔可夫链进行建模的生成模型，如下图所示：

在隐马尔科夫模型中，包含隐状态 和 观察状态，隐状态 $x_i$ 对于观察者而言是不可见的，而观察状态 $y_i$ 对于观察者而言是可见的。隐状态间存在转移概率，隐状态 $x_i$到对应的观察状态 $y_i$ 间存在输出概率。

假设

1. 假设隐状态 $x_i$ 的状态满足马尔可夫过程，i时刻的状态 $x_i$ 的条件分布，仅与其前一个状态 $x_{i-1}$相关，即：

$P(x_i|x_1,x_2,...,x_{i-1}) = P(x_i|x_{i-1})$

2. 假设观测序列中各个状态仅取决于它所对应的隐状态，即：

$P(y_i|x_1,x_2,...,x_{i-1},y_1,y_2,...,y_{i-1},y_{i+1},...) = P(y_i|x_{i})$

存在问题

在序列标注问题中，隐状态（标注）不仅和单个观测状态相关，还和观察序列的长度、上下文等信息相关。例如词性标注问题中，一个词被标注为动词还是名词，不仅与它本身以及它前一个词的标注有关，还依赖于上下文中的其他词。

条件随机场 （以线性链条件随机场为例）

定义

给定 $X=(x_1,x_2,...,x_n)$ ， $Y=(y_1,y_2,...,y_n)$ 均为线性链表示的随机变量序列，若在给随机变量序列 X 的条件下，随机变量序列 Y 的条件概率分布 $P(Y|X)$ 构成条件随机场，即满足马尔可夫性：

扫描二维码关注公众号，回复： 11165287 查看本文章

$P(y_i|x_1,x_2,...,x_{i-1},y_1,y_2,...,y_{i-1},y_{i+1}) = P(y_i|x,y_{i-1},y_{i+1})$

则称为 $P(Y|X)$ 为线性链条件随机场。

通过去除了隐马尔科夫算法中的观测状态相互独立假设，使算法在计算当前隐状态 $x_i$时，会考虑整个观测序列，从而获得更高的表达能力，并进行全局归一化解决标注偏置问题。

参数化形式

$p\left(y | x\right)=\frac{1}{Z\left(x\right)} \prod_{i=1}^{n} \exp \left(\sum_{i, k} \lambda_{k} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right)$

其中：

$Z(x)$ 为归一化因子，是在全局范围进行归一化，枚举了整个隐状态序列 $x_{1…n}$的全部可能，从而解决了局部归一化带来的标注偏置问题。

$Z(x)=\sum_{y} \exp \left(\sum_{i, k} \lambda_{x} t_{k}\left(y_{i-1}, y_{i}, x, i\right)+\sum_{i, l} \mu_{l} s_{l}\left(y_{i}, x, i\right)\right)$

$t_k$ 为定义在边上的特征函数，转移特征，依赖于前一个和当前位置

$s_1$ 为定义在节点上的特征函数，状态特征，依赖于当前位置。

简化形式

因为条件随机场中同一特征在各个位置都有定义，所以可以对同一个特征在各个位置求和，将局部特征函数转化为一个全局特征函数，这样就可以将条件随机场写成权值向量和特征向量的内积形式，即条件随机场的简化形式。

step 1

将转移特征和状态特征及其权值用统一的符号表示，设有k1个转移特征， $k_2$个状态特征， $K=k_1+k_2$,记

$f_{k}\left(y_{i-1}, y_{i}, x, i\right)=\left\{\begin{array}{lc} t_{k}\left(y_{i-1}, y_{i}, x, i\right), & k=1,2, \cdots, K_{1} \\ s_{l}\left(y_{i}, x, i\right), & k=K_{1}+l ; l=1,2, \cdots, K_{2} \end{array}\right.$

step 2

对转移与状态特征在各个位置i求和，记作

$f_{k}(y, x)=\sum_{i=1}^{n} f_{k}\left(y_{i-1}, y_{i}, x, i\right), \quad k=1,2, \cdots, K$

step 3

将 $\lambda_{x}$ 和 $\mu_{l}$ 用统一的权重表示，记作

$w_{k}=\left\{\begin{array}{ll} \lambda_{k}, & k=1,2, \cdots, K_{1} \\ \mu_{l}, & k=K_{1}+l ; l=1,2, \cdots, K_{2} \end{array}\right.$

step 4

转化后的条件随机场可表示为：

$\begin{aligned} P(y | x) &=\frac{1}{Z(x)} \exp \sum_{k=1}^{K} w_{k} f_{k}(y, x) \\ Z(x) &=\sum_{y} \exp \sum_{k=1}^{K} w_{k} f_{k}(y, x) \end{aligned}$

step 5

若 $w$ 表示权重向量：

$w = (w_1,w_2,...,w_K)^T$

以 $F(y,x)$ 表示特征向量，即

$F(y, x)=\left(f_{1}(y, x), f_{2}(y, x), \cdots, f_{K}(y, x)\right)^{\mathrm{T}}$
则，条件随机场写成内积形式为：

$\begin{array}{c} P_{w}(y | x)=\frac{\exp (w \cdot F(y, x))}{Z_{w}(x)} \\ Z_{w}(x)=\sum_{y} \exp (w \cdot F(y, x)) \end{array}$

学习问题

这里主要介绍一下 BFGS 算法的思路。

输入：特征函数 $f_1,f_2,...,f_n$：经验分布 $\widetilde{P}(X,Y)$；

输出：最优参数值 $\widehat{w}$，最优模型 $P_{\widehat{w}}(y|x)$。

1. 选定初始点 w^{(0)}， 取 $B_0$ 为正定对称矩阵，k = 0;
2. 计算 $g_k = g(w^(k))$，若 $g_k = 0$ ，则停止计算，否则转 (3) ；
3. 利用 $B_k p_k = -g_k$ 计算 $p_k$；
4. 一维搜索：求 $\lambda_k$使得

$f\left(w^{(k)}+\lambda_{k} p_{k}\right)=\min _{\lambda>0} f\left(w^{(k)}+\lambda p_{k}\right)$

5. 设 $w^{(k+1)} = w^{(k)} + \lambda_k * p_k$

6. 计算 $g_{k+1}$ = g(w^{(k+1)}),

   若 $g_k = 0$， 则停止计算；否则，利用下面公式计算 $B_{k+1}$:

$\begin{aligned} &B_{k+1}=B_{k}+\frac{y_{k} y_{k}^{\mathrm{T}}}{y_{k}^{\mathrm{T}} \delta_{k}}-\frac{B_{k} \delta_{k} \delta_{k}^{\mathrm{T}} B_{k}}{\delta_{k}^{\mathrm{T}} B_{k} \delta_{k}}\\ &y_{k}=g_{k+1}-g_{k}, \quad \delta_{k}=w^{(k+1)}-w^{(k)} \end{aligned}$
7. 令 $k=k+1$，转步骤（3）；

预测问题

对于预测问题，常用的方法是维特比算法，其思路如下：

输入：模型特征向量 $F(y,x)$ 和权重向量 $w$，输入序列（观测序列） $x={x_1,x_2,...,x_n}$；

输出：条件概率最大的输出序列（标记序列） $y^{*}= (y_1^*,y_2^*,...,y_n^*)$，也就是最优路径；

1. 初始化

$\delta_{1}(j)=w \cdot F_{1}\left(y_{0}=\operatorname{start}, y_{1}=j, x\right), \quad j=1,2, \cdots, m$
$\Psi_{i}(l)=\arg \max _{1 \leqslant j \leqslant m}\left\{\delta_{t-1}(j)+w \cdot F_{i}\left(y_{i-1}=j, y_{i}=l, x\right)\right\}, \quad l=1,2, \cdots, m$

2. 递推，对 $i=2,3,...,n$

$\delta_{i}(l)=\max _{1 \in j \leqslant m}\left\{\delta_{t-1}(j)+w \cdot F_{i}\left(y_{i-1}=j, y_{i}=l, x\right)\right\}, \quad l=1,2, \cdots, m$

3. 终止

$\begin{array}{c} \max _{y}(w \cdot F(y, x))=\max _{1 \leq j \leqslant m} \delta_{n}(j) \\ y_{n}^{*}=\arg \max _{1 \leqslant j \leqslant m} \delta_{n}(j) \end{array}$

4. 返回路径

$y_{i}^{*}=\Psi_{i+1}\left(y_{i+1}^{*}\right), \quad i=n-1, n-2, \cdots, 1$

求得最优路径 $y^{*}= (y_1^*,y_2^*,...,y_n^*)$

例子说明

利用维特比算法计算给定输入序列 $x$ 对应的最优输出序列 $y^*$：

$\max \sum_{i=1}^{3} w \cdot F_{i}\left(y_{i-1}, y_{i}, x\right)$

1. 初始化

$\begin{array}{l} \delta_{1}(j)=w \cdot F_{1}\left(y_{0}=\operatorname{start}, y_{1}=j, x\right), \quad j=1,2 \\ i=1, \quad \delta_{1}(1)=1, \quad \delta_{1}(2)=0.5 \end{array}$

2. 递推，对 $i=2,3,...,n$

$\begin{array}{c} i=2 \quad \delta_{2}(l)=\max \left\{\delta_{1}(j)+w \cdot F_{2}(j, l, x)\right\} \\ \delta_{2}(1)=\max \left\{1+\lambda_{2} t_{2}, 0.5+\lambda_{4} t_{4}\right\}=1.6, \quad \Psi_{2}(1)=1 \\ \delta_{2}(2)=\max \left\{1+\lambda_{1} t_{1}+\mu_{2} s_{2}, 0.5+\mu_{2} s_{2}\right\}=2.5, \quad \Psi_{3}(2)=1 \\ i=3^{2} \delta_{3}(l)=\max _{j}\left\{\delta_{2}(j)+w \cdot F_{3}(j, l, x)\right\} \\ \delta_{3}(1)=\max \left\{1.6+\mu_{5} s_{5}, 2.5+\lambda t_{3}+\mu_{3} s_{3}\right\}=4.3, \quad \Psi_{3}(1)=2 \\ \delta_{3}(2)=\max \left\{1.6+\lambda t_{1}+\mu_{4} s_{4}, 2.5+\lambda_{5} t_{5}+\mu_{4} s_{4}\right\}=3.2, \quad \Psi_{3}(2)=1 \end{array}$

3. 终止

$\begin{array}{c} \max _{y}(w \cdot F(y, x))=\max \delta_{3}(l)=\delta_{3}(1)=4.3 \\ y_{3}^{*}=\arg \max _{1} \delta_{3}(l)=1 \end{array}$
4. 返回路径

$\begin{array}{l} y_{2}^{*}=\Psi_{3}\left(y_{3}^{*}\right)=\Psi_{3}(1)=2 \\ y_{1}^{*}=\Psi_{2}\left(y_{2}^{*}\right)=\Psi_{2}(2)=1 \end{array}$

求得最优路径 $y^{*}= (y_1^*,y_2^*,...,y_n^*) = (1,2,1)$