关于树状数组
树状数组,即 Binary Indexed Tree ,主要用于维护查询区间和
属于 log 型数据结构
和线段树比较
都是 log 级别
树状数组常数、耗费的空间都比线段树小
树状数组无法完成复杂的区间操作,功能有限
树状数组介绍
二叉树大家一定不陌生

然而真实的树状数组省去了一些空间
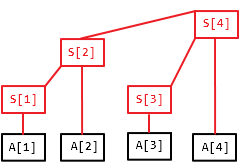
其中黑色的是原数组,红色的是树状数组
根据图可以看出 S[] 的由来
S[1] = A[1]
S[2] = A[1] + A[2]
S[3] = A[3]
S[4] = A[1] + A[2] + A[3] + A[4]
按照上面的规律:
S[5] = A[5]
S[6] = A[5] + A[6]
······
可以发现:这颗树是有规律的
S[i] = A[i-2k+1] + A[i-2k+2] + ··· + A[i]
其中 k 是 i 在 2 进制下末尾连续 0 的个数
比如 i=4=100(2) 则 k=2
那如何求和呢,如要求位置 6 的和,就应该是 S[6]+S[4]
根据上式可以算出每个位置的前缀和 V[i]=S[i]+S[i-2k1]+S[(i-2k1)-2k2]+ ···
新的问题来了: 2k 怎么求?
有两种方法: i&(i^(i-1)) 和 i&-i ,他们统一叫做 lowbit
lowbit 原理
lowbit 相当于求二进制从末尾到第一个 1 这一段
如 lowbit(1010B)=10B
方法 1
i-1 就是 i 在二进制中从末尾到末尾第一个 1 全部取反
如 20D=10100B 19D=10011B
把它们位异或一下,使得末尾有若干个 1 ,并去掉了前面相同的部分,如 10100B^10011B=00111B
再与原数位与一下,由于除了原数末尾第一个 1 以外都不同,所以其余都是 0
如 10100B&00111B=100B ,就是 lowbit 了
方法 2
然而现实中用的更多还是这个也许这个好记
-x 即为 x 的反码加一
而反码在加一时由于取反了,后面有一段都是 1 ,所以就会一直进位直到遇到 0 并使其变成 1
由于取反了,只有那一位 1 是相同的,这样只要位与一下,只留下那个 1 就行了
树状数组的操作
既然 get 到了精髓,后面的操作也简单了许多
约定
| 变量名 | 意义 |
|---|---|
| n | 原数组长度 |
| t[] | 树状数组 |
单点修改
上面说了 S[i] = A[i-2k+1] + A[i-2k+2] + ··· + A[i]
那既然 A[i] 修改了, S[i+2k] 、 S[i+2k+2k] ··· 都被修改了
inline void add(int p,int v){
for(;p<=n;p+=p&-p)
t[p]+=v;
}
单点查询
前面也给出公式了,直接循环
inline int sum(int p){
register int ans=0;
for(;p>0;p-=p&-p)
ans+=t[p];
return ans;
}
区间查询
有了前缀和自然可以求区间和
直接返回sum(r)-sum(l-1)
例题
单点修改 + 区间查询
洛谷 P3374
前面已经讲过了
#include<bits/stdc++.h>
using namespace std;
inline char nc(){
static char buf[100000],*S=buf,*T=buf;
return S==T&&(T=(S=buf)+fread(buf,1,100000,stdin),S==T)?EOF:*S++;
}
inline int read(){
static char c=nc();register int f=1,x=0;
for(;c>'9'||c<'0';c=nc()) c==45?f=-1:1;
for(;c>'/'&&c<':';c=nc()) x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
char fwt[100000],*ohed=fwt;
const char *otal=ohed+100000;
inline void pc(char ch){
if(ohed==otal) fwrite(fwt,1,100000,stdout),ohed=fwt;
*ohed++=ch;
}
inline void write(int x){
if(x<0) pc('-'),x=-x;
if(x>9) write(x/10);
pc(x%10+'0');
}
int n,m,opt,x,y,t[500002];
inline void add(int p,int v){
for(;p<=n;p+=p&-p)
t[p]+=v;
}
inline int sum(int p){
register int ans=0;
for(;p>0;p-=p&-p)
ans+=t[p];
return ans;
}
int main(){
n=read(),m=read();
for(register int i=1;i<=n;i++){
x=read();
add(i,x);
}
while(m--){
opt=read(),x=read(),y=read();
if(opt==1) add(x,y);
else write(sum(y)-sum(x-1)),pc('\n');
}
fwrite(fwt,1,ohed-fwt,stdout);
}
区间修改 + 单点查询
虽然看上去没大变化,但是如果按照之前的思路,复杂度为 \(O(mn\ log\ n)\) ,比普通数组还差
所以需要运用差分的思想,设 d[i] 为 a[i] 的差分数组,且 d[i]=a[i]-a[i-1]
那么 \(a_i = \sum\limits_{j=1}^i d_j\)
因为是单点查询,所以我们考虑直接维护 d 这个数组的前缀和
怎么区间修改?运用差分思想,可以先从 l 开始加上那个值,再从 r 开始减去那个值,最后求和时就相当于区间修改了
洛谷 P3368
#include<bits/stdc++.h>
using namespace std;
inline char gc(){
static char buf[100000],*S=buf,*T=buf;
return S==T&&(T=(S=buf)+fread(buf,1,100000,stdin),S==T)?EOF:*S++;
}
inline int read(){
static char c=gc();register int f=1,x=0;
for(;c>'9'||c<'0';c=gc()) c==45?f=-1:1;
for(;c>'/'&&c<':';c=gc()) x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
char fwt[100000],*ohed=fwt;
const char *otal=ohed+100000;
inline void pc(char ch){
if(ohed==otal) fwrite(fwt,1,100000,stdout),ohed=fwt;
*ohed++=ch;
}
inline void write(int x){
if(x<0) x=-x,pc('\n');
if(x>9) write(x/10);
pc(x%10+'0');
}
int n,m,opt,x,y,k,lst,t[500002];
inline void add(int p,int v){
for(;p<=n;p+=p&-p)
t[p]+=v;
}
inline int sum(int p){
register int ans=0;
for(;p>0;p-=p&-p)
ans+=t[p];
return ans;
}
int main(){
n=read(),m=read();
for(register int i=1;i<=n;i++){
x=read();
add(i,x-lst);
lst=x;
}
while(m--){
opt=read(),x=read();
if(opt==1){
y=read(),k=read();
add(x,k),add(y+1,-k);
}
else write(sum(x)),pc('\n');
}
fwrite(fwt,1,ohed-fwt,stdout);
}
区间修改 + 区间查询
还是运用差分思想,但是如何在差分数组中求前缀和呢?
已知 \(sum_i = \sum\limits_{j=1}^i a_j\)
把 a[j] 换成差分数组,得到 \(sum_i = \sum\limits_{j=1}^i \sum\limits_{k=1}^j d_k\)
可以看出每个元素出现的次数是递减的,变换一下,得 \(i*(d_1+d_2+d_3+···)-(0*d_1+1*d_2+2*d_3+···)\)
写成求和公式: \((i*\sum\limits_{j=1}^i d_j)-(\sum\limits_{j=1}^i (j-1)*d_j)\)
这时我们发现:后面那一部分可以用树状数组存下来,快速求和
洛谷 P3372
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline char gc(){
static char buf[100000],*S=buf,*T=buf;
return S==T&&(T=(S=buf)+fread(buf,1,100000,stdin),S==T)?EOF:*S++;
}
inline ll read(){
static char c=gc();register ll f=1,x=0;
for(;c>'9'||c<'0';c=gc()) c==45?f=-1:1;
for(;c>'/'&&c<':';c=gc()) x=(x<<3)+(x<<1)+(c^48);
return x*f;
}
char fwt[100000],*ohed=fwt;
const char *otal=ohed+100000;
inline void pc(char ch){
if(ohed==otal) fwrite(fwt,1,100000,stdout),ohed=fwt;
*ohed++=ch;
}
inline void write(ll x){
if(x<0) x=-x,pc('\n');
if(x>9) write(x/10);
pc(x%10+'0');
}
ll x,y,ls,rs,tmp,t1[100005],t2[100005];
int n,m,opt,lst,k;
inline void add(int p,int v,ll t[]){
for(;p<=n;p+=p&-p)
t[p]+=v;
}
inline ll sum(int p,ll t[]){
ll ans=0;
for(;p>0;p-=p&-p)
ans+=t[p];
return ans;
}
int main(){
n=read(),m=read();
for(register int i=1;i<=n;i++){
x=read(),tmp=x-lst;
add(i,tmp,t1);
add(i,tmp*(i-1),t2);
lst=x;
}
while(m--){
opt=read(),x=read(),y=read();
if(opt==1){
k=read();
add(x,k,t1);
add(x,k*(x-1),t2);
add(y+1,-k,t1);
add(y+1,-k*y,t2);
}
else{
rs=y*sum(y,t1)-sum(y,t2);
ls=(x-1)*sum(x-1,t1)-sum(x-1,t2);
write(rs-ls),pc('\n');
}
}
fwrite(fwt,1,ohed-fwt,stdout);
}
The End