FFT在matlab中的使用方法

FFT在matlab中的用法

一、FFT的物理意义

​ FFT是离散傅立叶变换的快速算法，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外，FFT可以将一个信号的频谱提取出来，这在频谱分析方面也是经常用的。 虽然很多人都知道FFT是什么，可以用来做什么，怎么去做，但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。 一个模拟信号，经过ADC采样之后，就变成了数字信号。采样定理告诉我们，采样频率要大于信号频率的两倍，这些我就不在此罗嗦了。 采样得到的数字信号，就可以做FFT变换了。N个采样点，经过FFT之后，就可以得到N个点的FFT结果。为了方便进行FFT运算，通常N取2的整数次方。

二、计算序列的FFT变换

求序列{2，3，3，2}的DFT变换。

>> N=4;
>> n=0:N-1;
>> xn=[2 3 3 2];
>> xk=fft(xn)

运算结果如下：

xk =

      10.0000 + 0.0000i  -1.0000 - 1.0000i   0.0000 + 0.0000i  -1.0000 + 1.0000i

带入公式检验：
$X[k]=\sum_{n=0}^{N-1}X[n]W_N^{nk}$

$X[0]=2W_4^{0}+3W_4^{0}+3W_4^{0}+2W_4^{0}=10$

$X[1]=2W_4^{0}+3W_4^{1}+3W_4^{2}+2W_4^{3}=-1-i$

$X[2]=2W_4^{0}+3W_4^{2}+3W_4^{4}+2W_4^{6}=0$

$X[3]=2W_4^{0}+3W_4^{3}+3W_4^{6}+2W_4^{9}=-1+i$

公式运算结果与matlab仿真结果一致。

​ xk与xn的维数相同，共有4个元素。xk的第一个数对应于直流分量，即频率值为0，在傅里叶级数的叠加中，它仅仅影响全部波形相对于数轴整体向上或是向下而不改变波的形状。

三、计算三角信号的FFT变换

1、分析采样点N的数量对FFT结果的影响

​ 做n个点的FFT，表示在时域上对原来的信号取了n个点来做频谱分析，n点FFT变换的结果仍为n个点。

信号一：y=0.5sin(2pi20t)+2sin(2pi40t)

​ 可以很容易的看出信号的由频率为20和40的两个分量组成，其中最高频率为40，根据奈科斯特定律，

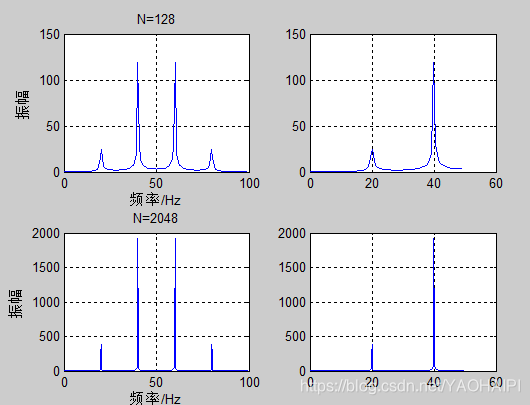
在这里我将抽样信号fs设定为100HZ，采样点N分别设定为128和2048。

​ N=128

>> fs=100;
>> N=128;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
>> x=fft(y,N);
>> m=abs(x);
>> f=n*fs/N;
>> subplot(2,2,1),plot(f,m);
>> xlabel('频率/Hz');
>> ylabel('振幅');title('N=128');
>> grid on;
>> subplot(2,2,2),plot(f(1:N/2),m(1:N/2));
>> grid on;

​ N=2048

>> fs=100;
>> N=2048;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
>> x=fft(y,N);
>> m=abs(x);
>> f=n*fs/N;
>> subplot(2,2,3),plot(f,m);
>> xlabel('频率/Hz');
>> ylabel('振幅');title('N=2048');
>> grid on;
>> subplot(2,2,4),plot(f(1:N/2),m(1:N/2));
>> grid on;

分析结果：

​ 这里的fs是采样频率。而我们通常只关心0-pi中的频谱，因为根据奈科斯特定律，只有f=fs/2范围内的信号才是被采样到的有效信号。那么，在w的范围内，得到的频谱肯定是关于n/2对称的。

​ 用100Hz做了128个点FFT之后，因为频率分辨率是100/128（25/32）Hz，如果原来的信号在2Hz或者1Hz有分量，你在频谱上是看不见的，这就表示你越想频谱画得逼真，就必须取越多的点数来做FFT，n就越大，你在时域上就必须取更长的信号样本来做分析。但是无论如何，由于离散采样的原理，你不可能完全准确地画出原来连续时间信号的真实频谱，只能无限接近（就是n无限大的时候），这个就叫做频率泄露。在采样频率fs不变得情况下，频率泄漏可以通过取更多的点来改善，也可以通过做FFT前加窗来改善，这就是另外一个话题了。

​ 第k个点的实际频率的计算为f(k)=k*(fs/n)

运行结果：

2、对FFT输出结果的探究

​ 从上一节“分析采样点N的数量对FFT结果的影响”我们可以看出不管采样点数目是多少，其频率为20的分量和频率为40的分量的振幅之比依然是1：4。这是为什么呢？我们知道FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值，就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢？

信号二：y=2+0.5sin(2pi20t)+2sin(2pi40t)

我以128HZ的采样频率对其采样，采样点N=128。我们的信号有3个频率分量0HZ、20HZ、40HZ。

>> fs=128;
>> N=128;
>> n=0:N-1;
>> t=n/fs;
>> y=2+0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
>> x=fft(y,N)

输出结果：

x =

   1.0e+02 *

  Columns 1 through 7

   2.5600 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i

  Columns 8 through 14

  -0.0000 + 0.0000i  -0.0000 - 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i  -0.0000 - 0.0000i

  Columns 15 through 21

   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i  -0.0000 + 0.0000i   -0.0000 - 0.3200i

  Columns 22 through 28

   0.0000 - 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i

  Columns 29 through 35

   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i

  Columns 36 through 42

   0.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 1.2800i   0.0000 - 0.0000i

  Columns 43 through 49

   0.0000 - 0.0000i   0.0000 - 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i  -0.0000 + 0.0000i

  Columns 50 through 56

   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i

  Columns 57 through 63

  -0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 - 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i

  Columns 64 through 70

   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 - 0.0000i

  Columns 71 through 77

   0.0000 - 0.0000i  -0.0000 + 0.0000i  -0.0000 - 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i

  Columns 78 through 84

   0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i

  Columns 85 through 91

  -0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 1.2800i   0.0000 - 0.0000i   0.0000 - 0.0000i

  Columns 92 through 98

  -0.0000 - 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i  -0.0000 + 0.0000i  -0.0000 - 0.0000i

  Columns 99 through 105

   0.0000 - 0.0000i  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 - 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i

  Columns 106 through 112

   0.0000 - 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.3200i  -0.0000 - 0.0000i   0.0000 + 0.0000i   0.0000 - 0.0000i

  Columns 113 through 119

  -0.0000 + 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 + 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 + 0.0000i

  Columns 120 through 126

  -0.0000 + 0.0000i  -0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i   0.0000 + 0.0000i  -0.0000 - 0.0000i   0.0000 - 0.0000i

  Columns 127 through 128

   0.0000 + 0.0000i  -0.0000 + 0.0000i

可以发现：

第1个点：2.5600 + 0.0000i 模值256

第2个点：-0.0000 - 0.0000i

第20个点：-0.0000 + 0.0000i

第21个点： -0.0000 - 0.3200i 模值32

第22个点：-0.0000 + 0.0000i

第40个点：0.0000 + 0.0000i

第41个点：-0.0000 - 1.2800i 模值128

第42个点：0.0000 + 0.0000i

可以发现只有在第1、21、41点处才有幅值，画出其频谱图观察。

>> m=abs(x);
>> f=n*fs/N;
>> plot(f,m);
>> xlabel('频率/Hz');
>> ylabel('振幅');title('N=128');
>> grid on;

运行结果：

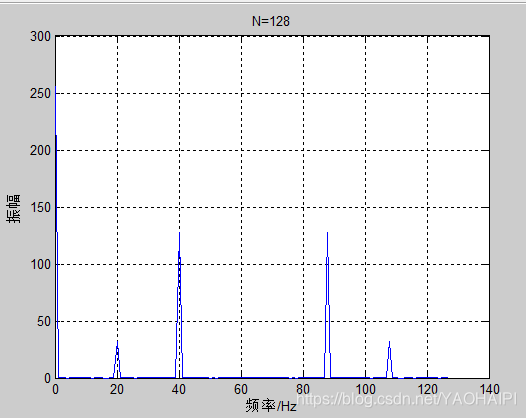
​ 可以看出频率0HZ、20HZ、40HZ对应点的幅值分别为256、36、128。这跟原始信号的幅度有什么关系呢？

结论：

​ 假设原始信号的峰值为A，那么FFT的结果的每个点（除了第一个点直流分量之外）的模值就是A的N/2倍。 而第一个点就是直流分量，它的模值就是直流分量的N倍。因此我们可以计算出原始信号的幅值。

根据公式：直流分量的真实幅值为256/128=2，正确

​ 20HZ分量的真实幅值为36/（128/2）=0.5，正确

​ 40HZ分量的真实幅值为128/（128/2）=2，正确

3、信号补零对FFT的影响

​ 在前面我们数据个数总是2得整数次幂，当数据个数不是2的整数次幂时会自动补零，以保持数据个数为2的整数次幂，那么补零会对FFT产生什么样的影响呢？

信号一：y=0.5sin(2pi20t)+2sin(2pi40t)

（1）数据个数N=32，FFT所用的采样点数NFFT=32；

>> fs=100;
>> N=32;
>> NFFT=32;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
>> x=fft(y,NFFT);
>> m=abs(x);
>> f=(0:NFFT-1)*fs/NFFT;
>> subplot(2,2,1),plot(f(1:NFFT/2),m(1:NFFT/2)*2/NFFT);
>> xlabel('频率/Hz');ylabel('振幅');
>> title('N=32 NFFT=32');grid on;

（2）数据个数N=32，FFT所用的采样点数NFFT=128；

>> N=32;
>> NFFT=128;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
>> x=fft(y,NFFT);
>> m=abs(x);
>> f=(0:NFFT-1)*fs/NFFT;
>> subplot(2,2,2),plot(f(1:NFFT/2),m(1:NFFT/2)*2/NFFT);
>> xlabel('频率/Hz');ylabel('振幅');
>> title('N=32 NFFT=128');grid on;

（3）数据个数N=300，FFT所用的采样点数NFFT=256；

>> N=300;
>> NFFT=256;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
>> x=fft(y,NFFT);
>> m=abs(x);
>> f=(0:NFFT-1)*fs/NFFT;
>> subplot(2,2,3),plot(f(1:NFFT/2),m(1:NFFT/2)*2/NFFT);
>> xlabel('频率/Hz');ylabel('振幅');
>> title('N=300 NFFT=256');grid on;

（4）数据个数N=140，FFT所用的采样点数NFFT=512。

>> N=140;
>> NFFT=512;
>> n=0:N-1;
>> t=n/fs;
>> y=0.5*sin(2*pi*20*t)+2*sin(2*pi*40*t);
>> x=fft(y,NFFT);
>> m=abs(x);
>> f=(0:NFFT-1)*fs/NFFT;
>> subplot(2,2,4),plot(f(1:NFFT/2),m(1:NFFT/2)*2/NFFT);
>> xlabel('频率/Hz');ylabel('振幅');
>> title('N=140 NFFT=512');grid on;

运行结果：

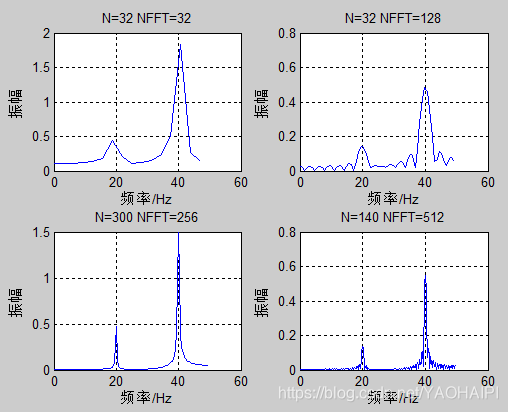
结论：

（1）当采样点数量为32时，由于数量比较少，频率分辨率比较低，画出的频谱图不是很逼真，但没有由于添零而导致的其他频率成分。

（2）由于采样点的数目比信号数据个数多，所以信号必须在时间域内加零。致使振幅谱中出现很多其他成分，这是加零造成的。其振幅由于加了多个零而明显减小。

（3）当数据个数超过频率采样点的个数时，FFT会自动切断。

（4）信号也在时域上补零了，但是由于数据的个数比较多，FFT振幅谱看起来比较逼真。

总结：

​ 如果采样数据比较少，运用FFT变换时，不能很准确的分辨出其中的频率成分。添加零后可增加频谱中的数据个数，谱的密度增高了，但仍不能分辨其中的频率成分，还会导致振幅的下降，即谱的分辨率没有提高。只有数据点数足够多时才能分辨其中的频率成分。