matlab克里格插值

前言

为履行前期承若，现在公开matlab的克里格插值的代码。

原理介绍

普通克里格法：假定 $Z(x)$是满足本征假设的一个随机过程，该随机过程有 $n$个观测值 $z(xi)$，要预测未采样点x0处的值，则线性预测值 $Z^{*}(x_0)$可以表示如下：
$Z^{*}(x_0)=\sum_{i=1}^n\lambda_iz(x_i)$
Kriging是在使预测无偏并有最小方差的基础上，去确定最优的权重值，满足以下两个条件：
(1)无偏性条件： $E[Z^{*}(x_0)-Z(x_))]=0$
(2)最优条件： $var[Z^*(x_0)-Z(x_0)]=min$
有如下
$E\left[Z^{*}\left(x_{0}\right)-Z\left(x_{0}\right)\right]=E\left[\sum_{i=1}^{n} \lambda_{i} z\left(x_{i}\right)-Z\left(x_{0}\right)\right]=\sum_{i=1}^{n} \lambda_{i} E\left[Z\left(x_{i}\right)\right]-E\left[Z\left(x_{0}\right)\right]$
根据本征假设 $E[Z(x_i)]=E[Z(x_0)]=m$
上式进一步表示：
$\sum_{i=1}^{n} \lambda_{i} E\left[Z\left(x_{i}\right)\right]-E\left[Z\left(x_{0}\right)\right]=\sum_{i=1}^{n} \lambda_{i} m-m=m\left(\sum_{i=1}^{n} \lambda_{i}-1\right)=0$
因此要满足如下条件：
$\sum_{i=1}^n\lambda_i=1$
普通克里格插值的条件如下：
1.在研究区域内，区域化变量 $Z(x)$的增量的数学期望对任意 $x$和 $h$存在且等于0
$E[Z(x)-Z(x+h)]=0$
2.在研究区域内，区域化变量的增量[ $Z(x)-Z(x+h)]$的方差对任意x和h存在且平稳
$\operatorname{Var}[Z(x)-Z(x+h)]=E\left[\{Z(x)-Z(x+h)\}^{2}\right]=2 r(h)$

在本证假设条件下
$\begin{array}{l} \operatorname{var}\left[Z^{*}\left(x_{0}\right)-Z\left(x_{0}\right)\right]=E\left[\left\{Z *\left(x_{0}\right)-Z\left(x_{0}\right)\right\}^{2}\right]=E\left[\left\{\sum_{i=1}^{n} \lambda_{i} z\left(x_{i}\right)-Z\left(x_{0}\right)\right\}^{2}\right] \\ =2 \sum_{i=0}^{n} \lambda_{i} \gamma\left(x_{i}, x_{0}\right)-\sum_{i=1}^{n} \sum_{j=1}^{n} \lambda_{i} \lambda_{j} \gamma\left(x_{i}, x_{j}\right) \end{array}$
根据方差最小原则，借助拉格朗日乘子，普通克里格的预测方程组为
$\left\{\begin{array}{l} \sum_{i=1}^{n} \lambda_{i}=1 \\ \sum_{i=1}^{n} \lambda_{i} \gamma\left(x_{i}, x_{j}\right)+\varphi\left(x_{0}\right)=\gamma\left(x_{j}, x_{0}\right) \end{array}\right.$
预测方差为
$\sigma^2(x_0)=\sum_{i=1}^n\lambda_i\gamma(x_i,x_0)+\phi$

克里格公式也可以用矩阵的形式表示，对点状克里格，有：
$A \bullet\left[\begin{array}{l} \lambda \\ \varphi \end{array}\right]=B$
对应的矩阵如下：
$\left[\begin{array}{ccccc} \gamma\left(s_{1}, s_{1}\right) & \gamma\left(s_{1}, s_{2}\right) & \cdots & \gamma\left(s_{1}, s_{n}\right) & 1 \\ \gamma\left(s_{2}, s_{1}\right) & \gamma\left(s_{2}, s_{2}\right) & \cdots & \gamma\left(s_{2}, s_{n}\right) & 1 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ \gamma\left(s_{n}, s_{1}\right) & \gamma\left(s_{n}, p_{2}\right) & \cdots & \gamma\left(p_{n}, s_{n}\right) & 1 \\ 1 & 1 & \cdots & 1 & 0 \end{array}\right] \times\left[\begin{array}{c} \lambda_{1} \\ \lambda_{2} \\ \vdots \\ \lambda_{n} \\ \mu \end{array}\right]=\left[\begin{array}{c} \gamma\left(s_{1}, s_{0}\right) \\ \gamma\left(s_{2}, s_{0}\right) \\ \vdots \\ \gamma\left(s_{n}, s_{0}\right) \\ 1 \end{array}\right]$

计算实例

以实验数据为例，对于不规则样点来进行克里格插值，首先要在预定的空间范围下设置网格，确定出左下角的xy起始坐标，将其进行坐标系平移，可以减少计算复杂度，将每个格网的中心点设置为待插值样点，以每个样点为待插值样点，搜索最近的 $n$个点，计算第 $i$行第 $j$列的格网的中心坐标是
$(xmin+gridsize/2+(j-1)*gridsize,ymin+gridsize/2+(m-i)*gridsize)$
基于我前面缩写mink函数搜索得到最近的 $n$个点，计算他们之间的距离代入到协方差函数之中
得到每个点的 $A$与 $B$矩阵，基于矩阵左除的方法对齐进行求解 $\lambda、\mu$
结果展示

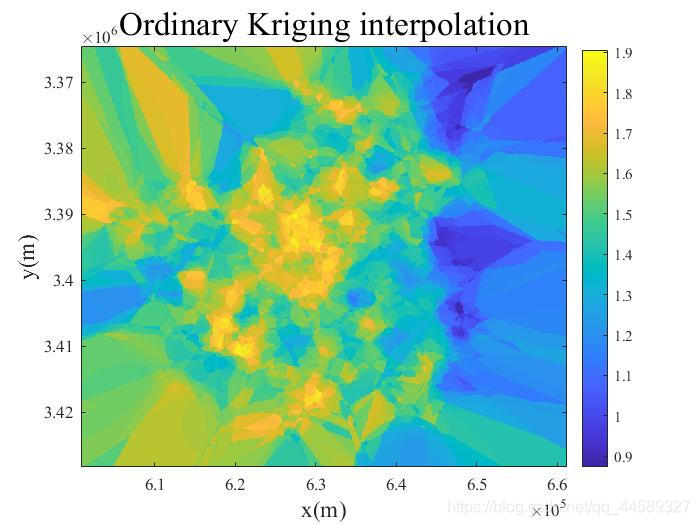
最终插值效果如上图所示

总结

本次总结主要在代码的简介度较高，以较快的速度来实现比较简单的克里格插值的这一算法。本次代码均在附录中展示，供大家学习，从代码层次对算法进一步了解。

附录

其中covfun_automatch函数需要自己写，根据自己变异函数模型来写对应的协方差函数

%输入插值格网大小girdsize，邻近点个数num_neighbor，插值的空间范围即沙洋县shp图层
%输入模型参数result_coef,其中1，2，3，4分别为c0,c1,a,m,块金值，基态值，变程，模型参数(1为球状，2为指数，3为高斯)
clear;
clc;
digits(20);   %设定默认的精度
tic;
result_coef=[0.0377,0.0814,42541,2];num_neighbor=4;gridsize=100;%输入参数
data=xlsread('F:\geostatistical_test\test\data_and_materials\delete_repeat.xlsx');
%data(:,1),data(:,2)对应于xy坐标，data(:,3)为对应的属性
Map=shaperead('F:\geostatistical_test\test\data_and_materials\沙洋边界\sy_xzbj.shp'); %读取沙洋县边获取空间范围
xyrange=[];
for i=1:size(Map,1)
    xyrange=[xyrange;Map(i).BoundingBox];
end
maxxy=max(xyrange);minxy=min(xyrange);xylength=maxxy-minxy;%xylength是最小外接矩形的长x和宽y
minx=minxy(1);miny=minxy(2);%取出最小xy坐标
data(:,1)=data(:,1)-minx;data(:,2)=data(:,2)-miny;%这一步是让左下角的xy坐标为0，这样计算距离就比较快
row_col=ceil(xylength./gridsize);%生成网格的大小，row_col(1)为所需列数，row_col(2)为所需行数
xc=zeros(row_col(2),row_col(1));yc=zeros(size(xc));%xc,yc分别存放格网中心的坐标xy
colmat=repmat(1:row_col(1),row_col(2),1);rowmat=repmat((1:row_col(2))',1,row_col(1));
xc=gridsize/2+(colmat-1).*gridsize;yc=gridsize/2+(row_col(2)-rowmat).*gridsize;
%这一行是将最小外接矩形的左下角xmin，ymin，与格网大小建立关系，在第i行第j列的格网的中心坐标是
% xmin+gridsize/2+(j-1)*gridsize,ymin+gridsize/2+(m-i)*gridsize,因为matlab索引从左上角开始，因此，是m-i
result=zeros(size(xc));sigma2=zeros(size(xc));
for i=1:row_col(2)
    for j=1:row_col(1)
        xy=[xc(i,j),yc(i,j)];%对第i，j个点寻找最近距离的点
        %计算样点离xy距离平方
        D2=(data(:,1)-xy(1)).^2+(data(:,2)-xy(2)).^2;
        [D,tag]=mink(D2,num_neighbor);%tag表示最近的4个点D表示对应的距离平方
        Dc_neighbor=sqrt(D);
        tag_neighbor=tag;
        %取出在邻域内的样点序号(tag_neighbor)以及对应插值点离样点的距离Dc_neighbor
        D_neighbor=squareform(pdist(data(tag,1:2)));
        %这一步利用的是matlab索引均为矢量的优势，会对里面矢量每个元素穷尽组合来组成矩阵，这里正好
        %可以生成插值点邻域内采样点点对之间的距离矩阵D_neighbor
        covD_neighbor=covfun_automatch(D_neighbor,result_coef);%生成采样点间对应的协方差矩阵
        covDc_neighbor=covfun_automatch(Dc_neighbor,result_coef);%%生成采样点与插值点之间对应的协方差矩阵
        A=[covD_neighbor,ones(size(covD_neighbor,1),1)];
        A=[A;ones(1,size(A,2))];
        A(end,end)=0;
        B=[covDc_neighbor;1];
        lambdau=A\B;%lambdau矩阵得到的最终的各个点的权重与u值
        lambda=lambdau(1:end-1);
        u=lambdau(end);
        result(i,j)=sum(lambda.*data(tag_neighbor,3));
        %这里soil_properties(tag_neighbor-1)减1的原因是前面距离矩阵上是加上了插值的点，因此要获取原始的
        %在data数据里的索引只需要将每个tag_neighbor-1即可
        sigma2(i,j)=mean(diag(covD_neighbor))-sum(lambda.*covDc_neighbor)+u;
        %克里格方差计算公式
    end
end
t=toc%运行时间
data_validij=[row_col(2)-round((data(:,2)-gridsize/2)./gridsize),round((data(:,1)-gridsize/2)./gridsize)+1];
%求出验证点对应的在格网中的行列号i，j索引，第一列为i，第二列为j
valid_predict_result=diag(result(data_validij(:,1),data_validij(:,2)));%这里仍然利用的是matlab行列索引均为矢量的优势，这样对角线上的元素就是我们想要找到一一对应的元素
%因此要用到diag函数得到了验证点对应的插值结果
valid_actual_value=data(:,3);%验证点的真实值
[R,RMSE,erroravg]=test_kriging(valid_actual_value,valid_predict_result);
%返回相关系数R，均方根误差RMSE，平均误差erroravg
figure;
imagesc([minx,minx+row_col(2)*gridsize],[miny,miny+row_col(1)*gridsize],result);colorbar;%定义xy范围画出工具条
title('Ordinary Kriging interpolation','FontSize',20);xlabel('x(m)','FontSize',14);ylabel('y(m)','FontSize',14);
set(gca,'Fontname','times new Roman');
figure;
imagesc([minx,minx+row_col(2)*gridsize],[miny,miny+row_col(1)*gridsize],sigma2);c1=colorbar;%定义xy范围画出工具条
title('Kriging Estimated Variance','FontSize',20);xlabel('x(m)','FontSize',14);ylabel('y(m)','FontSize',14);
set(gca,'Fontname','times new Roman');