文章目录
简介
最近越来越发现数学的重要性,几乎所有的问题都抽象成为一个复杂的模型,然后通过数学的技巧来进行转化,得到一个可以求解的数学问题。可见数学的重要性。
然后对于模式识别来说,数学更是解决问题的基础。这里我总结和罗列了一些数学基础方法。也算是给自己做一个总结。
牛顿迭代法近似求解方程根
应用:多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。方法使用函数f(x)的Taylor级数的前面几项来寻找方程f(x) = 0的根。
牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f(x) = 0的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根。该方法广泛应用于科学计算的计算机编程中。
具体方法:
设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0)+f’(x0)(x-x0),求出L与x轴交点的横坐标 x1 = x0-f(x0)/f’(x0),称x1为r的一次近似值。过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴交点的横坐标 x2 = x1-f(x1)/f’(x1),称x2为r的二次近似值。重复以上过程,得r的近似值序列,其中 :
x(k+1)=x(k)-f(x(k))/f’(x(k))
称为r的k+1次近似值,上式称为牛顿迭代公式。
解法:
解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。把f(x)在x0点附近展开成Taylor级数 f(x) = f(x0)+(x-x0)f‘(x0)+(x-x0)^2*f’(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即Taylor展开的前两项,则有f(x0)+f’(x0)(x-x0)=f(x)=0 。设f‘(x0)≠0,则其解为x1=x0-f(x0)/f’(x0) 。这样,得到牛顿法的一个迭代序列:x(k+1)=x(k)-f(x(k))/f’(x(k))。
梯度
应用:
在单变量的实值函数的情况,梯度就是导数。若实值函数为线性函数,梯度就是该直线的斜率。
在二元函数的情形,设函数z=f(x,y)在平面区域D内具有一阶连续偏导数,则f(x,y)在对应点P(x,y)∈D上的梯度为一个二维向量:

在工程应用中,为了方便起见,有时将梯度的幅度简称为梯度。
在图像处理与分析中,为了降低图像的运算量,常用绝对值代替平方根运算,即:

拉格朗日乘数法
应用:
在某些约束条件下,使函数f(x)取到极值的自变量x0的值。根据约束条件下的不同,可以分为如下几种情况:(1)一个等式约束方程的情况;(2)多个等式约束方程的情况;(3)多个不等式约束方程的情况。这里仅介绍第(1)种情况。
若约束条件可以表示可以表示为g(x)=0的形式,那么我们可按如下方法求出f(x)的极值。
首先,构造Lagrange函数:

然后,对Lagrange乘数关于x求偏导数,并令其值等于零:
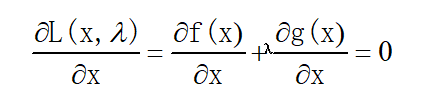
这样就把约束条件下的最优化问题转化为无约束条件的方程求解问题。
通过求解上面方程,就能得到λ的值及相应的极值点x0(通常情况下,λ∂g/∂x不等于0)。最后把x0代入到f(x)函数,就能得到约束条件下f(·)的极值。
Fish准则函数的机制求解

其中 Sw为类内离散度矩阵, Sb为类间离散度矩阵。
采用Langrage乘数法对J(W)求极值,以得到最优的权向量W*。
求解过程:



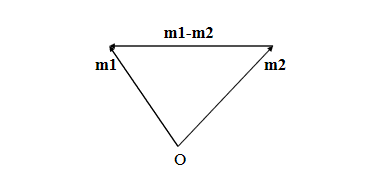

所以最终有:
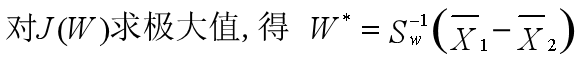
大家共勉~~
祝我早日开学