《Reinforcement Learning: An Introduction》 Chapter 2 Multi-arm Bandits 笔记

Sample-average Method

Sample-average Method 以平均值的方式描述了Q值：

\[Q_t(a) = \frac{R_1+R_2+...+R_{N_{t}(a)}}{N_{t}(a)} \]

\(N_t(a)\)表示动作a选被选择的次数。\(N_t(a)=0\)时，\(Q_t(a)\)为预定义一些初始值；\(N_t(a) \rightarrow \infty\)，根据大数定理，\(Q_t(a)\)收敛到动作a的实际值\(q(a)\)。

原文如下：

\(\epsilon-greedy\)

\(\epsilon-greedy\) 是以一个概率\(\epsilon\)选择非贪婪策略的动作。下图为\(\epsilon\)取不同值的效果图：

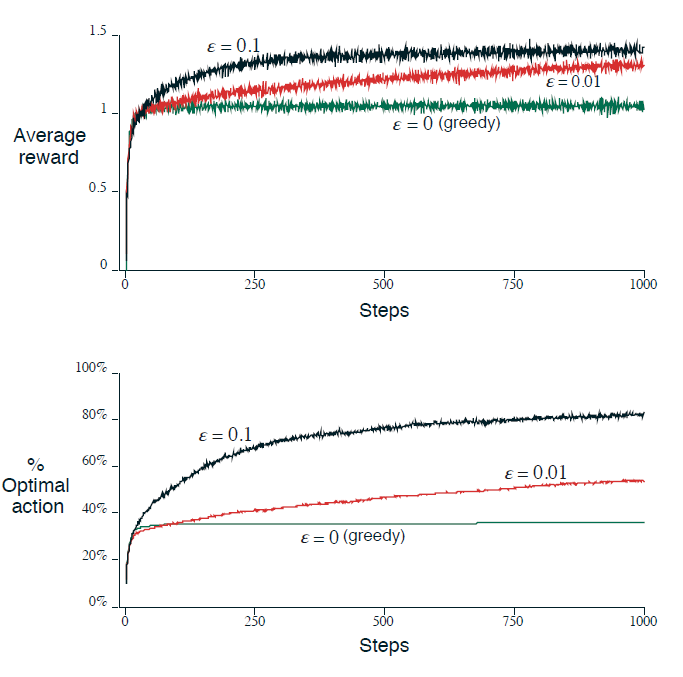
Notice that:

\(\epsilon=0.01\) 的效果提升很慢，但是最后效果会比 \(\epsilon=0.1\) 的效果要好。

（之前在Github随便找的一个代码的 \(\epsilon\) 是随迭代次数的增加而减少，最后为一个较小的固定值再迭代一定次数）

Incremental Implementation

给出了一个 Sample-average Method 的Q值递推式:

\[\begin{aligned} Q_{k+1}&=\frac{1}{k}\sum_{i=1}^kR_i\\ &=\frac{1}{k}\left(R_k+\sum_{i=1}^{k-1}R_i\right)\\ &=Q_k+\frac{1}{k}\Big[R_k-Q_k\Big] \end{aligned} \qquad （1） \]

一般形式：

\[NewEstimae \leftarrow OldEstimate + StepSize\Big[Target-OldEstimate\Big] \]

\([Target-OldEstimate]\)可以看做是估计误差。

Tracking a Nonstationary Problem

用step-size参数 \(\alpha \in (0,1]\) 替换\(\frac{1}{k}\),重写等式（1):

\[\begin{aligned} Q_{k+1} & = Q_k + \alpha \Big[R_k-Q_k \Big]\\ & = \alpha R_k + (1 - \alpha) Q_k\\ & = (1-\alpha)^kQ_1 + \sum_{i=1}^k\alpha(1-\alpha)^{k-i}R_i \end{aligned} \qquad （2） \]

Theorem 1

如果序列\(\{\alpha_k(a)\}\)满足以下条件，则等式（2）必收敛：

\[\sum_{k=1}^\infty\alpha_k(a)=\infty \quad and \quad \sum_{k=1}^\infty\alpha_k^2(a) \lt \infty （3） \]

第一个条件保证了步长足够大，以克服任意初始值。

第二个条件保证步长足够小，以保证收敛。

此处... 应该要有个Proof，但是呢... 他没写，俺也不知道，也不感兴趣。因为...

Note

通常， 满足条件（3）的步长序列收敛很慢或者需要大量调试才能获得一个较好的收敛速率。
并且，满足条件（3）的序列一般用于理论工作，几乎不在实践中使用。

Optimistic Initial Values

顾名思义，选择一个乐观的初始解。 性能对比图如下：

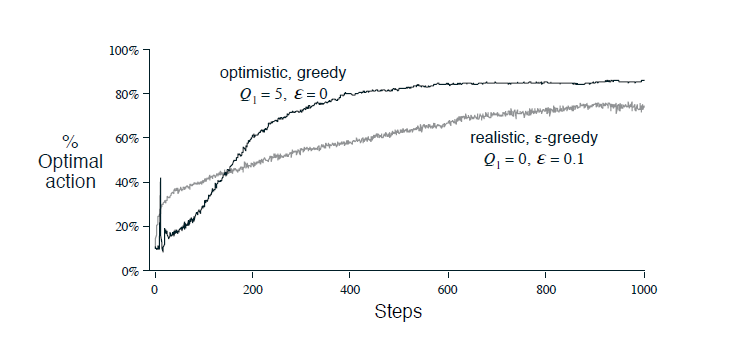
Note

这不是一个普遍有用的方法！！！ 比如，在不稳定问题上不太有用，因为它的探索动力本质上是暂时的（我的理解，因为虽然拉高了初值，只会在开始后一段时间有点用吧，并没有在本质上增加探索。）

Upper-Confidence-Bound Action Selection

选择动作时，根据等式（4）：

\[A_t = \arg\max\limits_{a} \Bigg[Q_t(a) + c\sqrt{\frac{lnt}{N_t(a)}} \Bigg] \]

如果\(N_t(a)=0\),选取Q值最大的动作。

Why？

考虑整个强化学习过程，有以下两个Observation：

1. 设当前采取某个动作a，实际得到的reward是r。估计的reward为：\(r'=\frac{\sum reward_i}{N_t(a)}\),则有当\(N_t(a) \rightarrow +\infty\)时，\(r' \rightarrow r\)
2. 由于采取的是估计值，则一定存在一个差值\(\Delta\)，使得\(r'-\Delta \le r \le r' + \Delta\)。

UCB 假设每次获得的reward是\(r' + \Delta\)。根据reward估计值的计算公式可知：

1. 如果多采取一次动作a, \(\Delta\)会逐渐变小。\(（N_t(a)变大，r'更接近r）\)
2. 如果多采用其它动作\(a^-\), \(\Delta\)会逐渐变大。

根据Chernoff-Hoeffding Bound（\(P\{\vert \overline{X}-E(X) \vert \le \delta \} \ge 1-2e^{-2n\delta^2}\)）

令\(\delta=c\sqrt{\frac{lnt}{N_t(a)}}\)，\(P\{\vert r'-r \vert\ \le c\sqrt{\frac{lnt}{N_t(a)}}\} \ge 1 - \frac{2}{t^{2c^2}}\)
即 \(r'-\delta \le r \le r' + \delta\)以\(1 - \frac{2}{t^{2c^2}}\)的概率成立， \(t \uparrow\)，\(P \rightarrow 1\) （详细的话，参考这个网页）

Performance:

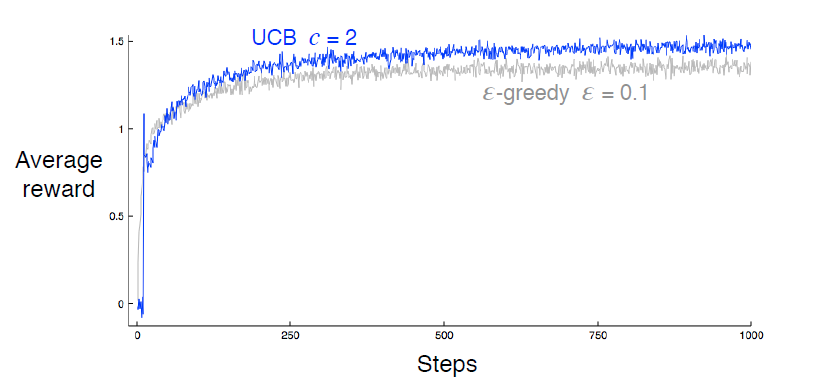
Gradient Bandits

本质是随机梯度上升。 改Q值为偏好度（preference）\(H_t(a)\)，根据概率进行动作选择，偏好度大的概率大。
概率计算公式如下：

\[Pr\{A_t = a\} = \frac{e^{H_t(a)}}{\sum_{b=1}^ne^{H_t(b)}}=\pi_t(a) \]

这里\(\pi_t(a)\)不表示策略，表示概率。
更新公式：

\[\begin{aligned} H_{t+1}(A_t) &= H_t(A_t) + \alpha(R_t - \overline{R_t})(1-\pi_t(A_t)), \\ H_{t+1}(a) &= H_t(a) + \alpha(R_t - \overline{R_t})\pi_t(a)), \quad \forall a \neq A_t. \end{aligned} \]

\(A_t\)为选择的动作。

证明过程就不写了，见书P57。 性能图如下：

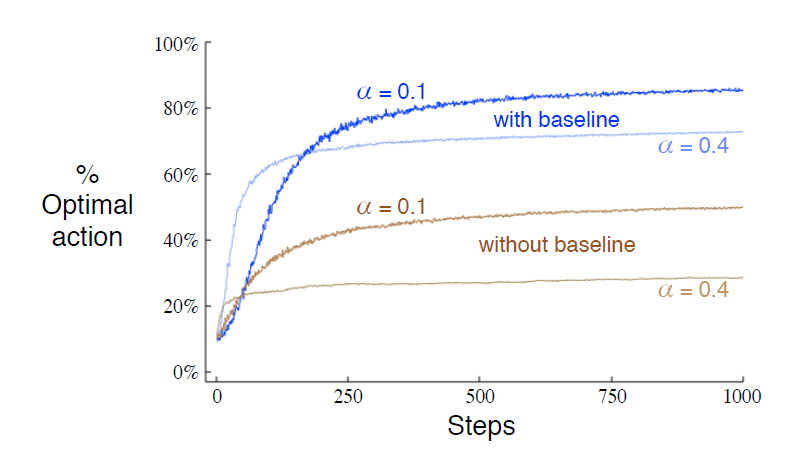
这里的baseline表示\(\overline{R_t}\)，without baseline就是\(\overline{R_t} = 0\)。

Summary

就贴个图吧

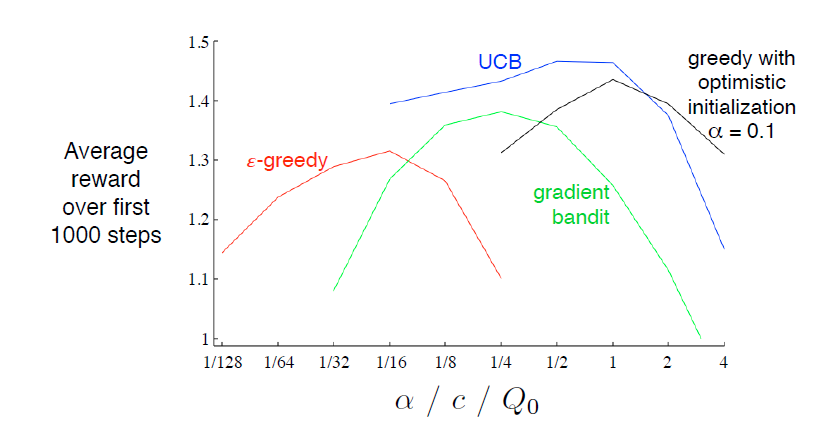
最后高亮了一句话，
In assessing an method, we should attend not just to how well it does at its best parameter setting, but also to how sensitive it is to its parameter value.