2020牛客暑期多校训练营（第一场）题解 Continue...

A B-Suffix Array

一.题目大意

\quad 对于字符串 $t_1{t}_2...t_k$，定义 $B(t_1{t}_2...t_k)=b_1{b}_2...b_k$

\quad \quad 如果存在 $j<i$ 且 $t_i=t_j$，则 $b_i=\underset{1\le j<i\le n,t_i=t_j}{\min }(i-j)$.

\quad \quad 否则，$b_i=0$.

\quad 给出字符串 $s=s_1{s}_2...s_n$，求 $s$ 的后缀所生成的函数 $B$ 的后缀数组.

\quad 1 ≤ n ≤ 1 0 5 , ∑ n ≤ 1 0 6 , t i ∈ { ′ a ′ , ′ b ′ } 1\leq n\leq 10^5, \sum n \leq 10^6, t_{i} \in \{'a','b'\} 1≤n≤105,∑n≤106,ti​∈{ ′a′,′b′}.

二.分析

\quad PPT题解做法自然不是我这等菜鸡能想到的，在这里讲一个我能想出来的做法吧.

\quad 首先，很容易想到：$s$ 的所有后缀的 $B$ 函数的结果中 $b_1$ 都为 $0$.

\quad 不失一般性，针对 $s$ 的第 $i$ 个后缀再延伸一下，不妨设 $s_i={}^{\prime }{a}^{\prime }$.

\quad 记 $p=\underset{i<j\le n,s_j={}^{\prime }{b}^{\prime }}{\min }(j-i+1)$，那么对于 $s$ 的第 $i$ 个后缀来说， $b_1{b}_2...b_{p-1}{b}_p=01...10$.

\quad 因此，我们把 $s$ 的第 $i$ 个后缀的函数 $B$ 的结果分为两部分 $X_i{Y}_i$，其中 $X_i=b_1{b}_2...b_p=01...10$，$Y_i=b_{p+1}...b_{n-i+1}$.

\quad 于是，当我们要比较 $B(s_i...s_n)$ 与 $B(s_j...s_n)$ 的字典序大小时，我们可以先比较 $X_i$ 和 $X_j$，若两者相同再去比较 $Y_i$ 和 $Y_j$.

\quad 由于 $X_i$ 的特性，不难得到：$X_i$ 与 $X_j$ 字典序的大小关系 $⟺$ $X_i$ 与 $X_j$ 长度的大小关系.

\quad 因此，我们可以预处理出以字符串 $s$ 的第 $i$ 个后缀开头的连续相同的子串的最长长度 + 1，记为 $dis[i]$，则 $dis[i]$ 即为 $X_i$ 的长度.

例如字符串 $s="aababbba"$，则 d i s [ ] = { 3 , 2 , 2 , 2 , 4 , 3 , 2 , 2 } dis[]=\{3, 2, 2, 2, 4, 3, 2, 2\} dis[]={ 3,2,2,2,4,3,2,2}.

\quad 由此，我们可以 $O(n)$ 预处理出 $dis[]$ 数组，$O(1)$ 查询 $X_i$ 与 $X_j$ 的字典序大小关系.

\quad 那么只有当 $X_i$ 与 $X_j$ 相等时，我们才去比较 $Y_i$ 与 $Y_j$. 但是怎样去比较 $Y_i$ 和 $Y_j$ 的关系呢？

\quad 不难理解，在 $X_i$ 等于 $X_j$ 的前提下，$B(s_i...s_n)$ 与 $B(s_j...s_n)$ 第一个不同的位置为 $B(s_i...s_n)[dis[i]+lcp]$ 和 $B(s_j...s_n)[dis[j]+lcp]$. 其中，$lcp$ 表示 $B(s_i...s_n)[dis[i]...n-i+1]$ 与 $B(s_j...s_n)[dis[j]...n-j+1]$ 的最长公共前缀的长度.

\quad 换句话说，在 $X_i$ 等于 $X_j$ 的前提下，$B(s_i...s_n)$ 与 $B(s_j...s_n)$ 第一个不同的位置为 $B(s_1...s_n)[i+dis[i]+lcp]$ 和 $B(s_1...s_n)[j+dis[j]+lcp]$. 其中，$lcp$ 表示 $B(s_1...s_n)[i+dis[i]...n-i+1]$ 与 $B(s_1...s_n)[j+dis[j]...n-j+1]$ 的最长公共前缀的长度. 思考一下，为什么这样是对的呢？

\quad 这是因为 $s[i+dis[i]-1]$ 是自 $s[i]$ 后面且与 $s[i]$ 不同的最近的一个字符，所以无论 $s_1...s_{i-1}$ 如何取值，都不会影响 $B(s_1...s_n)[i+dis[i]...n-i+1]$. 因而上面是成立的.

\quad 到这里，思路讲得就差不多了，说一下代码步骤：

\quad 1. 求出 $B(s_1{s}_2...s_n)$，记为数组 $b[]$.

\quad 2. 求出数组 $dis[]$.

\quad 3. 对编号数组 $ans[]$ 排序，当 $X_i\ne X_j$ 时，比较 $dis[i]$ 和 $dis[j]$；否则，比较 $B(s_1...s_n)[i+dis[i]+lcp]$ 和 $B(s_1...s_n)[j+dis[j]+lcp]$，其中 $lcp$ 表示 $B(s_1...s_n)[i+dis[i]...n-i+1]$ 与 $B(s_1...s_n)[j+dis[j]...n-j+1]$ 的最长公共前缀的长度，可通过后缀数组求得.

三.代码实现

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

const int M = (int)2e5;//M 应当开到最大字符串长度的两倍，否则(1)处下标访问可能越界。
const int Mlog = 20;

/*
1.  rk[i]表示下标i的排名（排名从0开始）。
2.  sa[i]表示第i小的后缀的下标（i从0开始）。
3.  height[i]表示sa[i - 1]与sa[i]的最长公共前缀。
*/
struct Suffix_Array
{
    
    
    int s[M + 5];
    int sa[M + 5], rk[M + 5], height[M + 5];
    int t[M + 5], t2[M + 5], c[M + 5], n;

    void init()
    {
    
    
        memset(t, 0, sizeof(int) * (2 * n + 10));//为了保证(1)处访问越界时得到的数组值恒为0，应当将t和t2数组清空
        memset(t2, 0, sizeof(int) * (2 * n + 10));
    }

    void build_sa(int m = 256)
    {
    
    
        int *x = t, *y = t2;
        for(int i = 0; i < m; ++i) c[i] = 0;
        for(int i = 0; i < n; ++i) c[x[i] = s[i]]++;
        for(int i = 1; i < m; ++i) c[i] += c[i - 1];
        for(int i = n - 1; i >= 0; --i) sa[--c[x[i]]] = i;
        for(int k = 1; k <= n; k <<= 1)
        {
    
    
            int p = 0;
            for(int i = n - 1; i >= n - k; --i) y[p++] = i;
            for(int i = 0; i < n; ++i) if(sa[i] >= k) y[p++] = sa[i] - k;
            for(int i = 0; i < m; ++i) c[i] = 0;
            for(int i = 0; i < n; ++i) c[x[y[i]]]++;
            for(int i = 1; i < m; ++i) c[i] += c[i - 1];
            for(int i = n - 1; i >= 0; --i) sa[--c[x[y[i]]]] = y[i];
            swap(x, y);
            p = 1;
            x[sa[0]] = 0;
            for(int i = 1; i < n; ++i)
                x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + k] == y[sa[i] + k] ? p - 1 : p++;//(1)
            if(p >= n) break;
            m = p;
        }
    }

    void get_height()
    {
    
    
        int k = 0;
        for(int i = 0; i < n; ++i) rk[sa[i]] = i;
        for(int i = 0; i < n; ++i)
        {
    
    
            if(rk[i] > 0)
            {
    
    
                if(k) --k;
                int j = sa[rk[i] - 1];
                while(i + k < n && j + k < n && s[i + k] == s[j + k]) ++k;
                height[rk[i]] = k;
            }
        }
    }

    int d[M + 5][Mlog + 5], Log[M + 5];

    void RMQ_init()
    {
    
    
        Log[0] = -1;
        for(int i = 1; i <= n; ++i) Log[i] = Log[i / 2] + 1;
        for(int i = 0; i < n; ++i) d[i][0] = height[i];
        for(int j = 1; j <= Log[n]; ++j)
        {
    
    
            for(int i = 0; i + (1<<j) - 1 < n; ++i)
            {
    
    
                d[i][j] = min(d[i][j - 1], d[i + (1<<(j-1))][j - 1]);
            }
        }
    }

    int lcp(int i, int j)//返回下标i开始的后缀与下标j开始的后缀的最长公共前缀。
    {
    
    
        if(i == j) return n - i;
        if(rk[i] > rk[j]) swap(i, j);
        int x = rk[i] + 1, y = rk[j];
        int k = Log[y - x + 1];
        return min(d[x][k], d[y - (1<<k) + 1][k]);
    }

    pair <int, int> Locate(int l, int r)//返回一个最长的区间[L, R]使得sa中下标从L到R的所有后缀都以s[l, r]为前缀。
    {
    
    
        int pos = rk[l], length = r - l + 1;
        int L = 0, R = pos, M;
        while(L < R)
        {
    
    
            M = (L + R) >> 1;
            if(lcp(l, sa[M]) >= length) R = M;
            else                        L = M + 1;
        }
        int tmp = L;
        L = pos, R = n - 1;
        while(L < R)
        {
    
    
            M = (L + R + 1) >> 1;
            if(lcp(l, sa[M]) >= length) L = M;
            else                        R = M - 1;
        }
        return make_pair(tmp, L);
    }
}SA;

int n; char s[M + 5];
int b[M + 5];
int dis[M + 5];
int ans[M + 5];

bool cmp(int i, int j)
{
    
    
    if(dis[i] != dis[j]) return dis[i] < dis[j];
    if(i + dis[i] >= n && j + dis[j] >= n) return i > j;
    if(i + dis[i] >= n)  return 1;
    if(j + dis[j] >= n)  return 0;
    int lcp = SA.lcp(i + dis[i], j + dis[j]);
    return b[i + dis[i] + lcp] < b[j + dis[j] + lcp];
}

void work()
{
    
    
    scanf("%s", s);
    int pa = -1, pb = -1; b[n] = 0;
    for(int i = 0; i < n; ++i)
    {
    
    
        if(s[i] == 'a')
        {
    
    
            if(~pa) b[i] = i - pa;
            else    b[i] = 0;
            pa = i;
        }
        else if(s[i] == 'b')
        {
    
    
            if(~pb) b[i] = i - pb;
            else    b[i] = 0;
            pb = i;
        }
    }
    SA.n = n;
    for(int i = 0; i < n; ++i) SA.s[i] = b[i];
    SA.init();
    SA.build_sa(n);
    SA.get_height();
    SA.RMQ_init();
    dis[n - 1] = 2;
    for(int i = n - 2; i >= 0; --i)
    {
    
    
        if(s[i] == s[i + 1]) dis[i] = dis[i + 1] + 1;
        else                 dis[i] = 2;
    }
    for(int i = 0; i < n; ++i) ans[i] = i;
    sort(ans, ans + n, cmp);
    for(int i = 0; i < n; ++i) printf("%d%c", ans[i] + 1, i == n - 1 ? '\n' : ' ');
}

int main()
{
    
    
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    while(~scanf("%d", &n)) work();
    return 0;
}

D Quadratic Form

一.题目大意

\quad 给定一个 $n\times n$ 的正定矩阵 $A$ 和一个大小为 $n$ 的列向量 $b$.

\quad 让你找出一个 $n$ 维列向量 $x=(x_1{x}_2...x_n)$，并且满足

\quad \quad 1. $x_1,x_2,...,x_n\in \mathbb{R}$.

\quad \quad 2. ${\sum }_{i=1}^n{\sum }_{j=1}^n{A}_{i,j}{x}_i{x}_j\le 1$.

\quad \quad 3. ${\sum }_{i=1}^n{b}_i{x}_i最大化$.

\quad 输出 $({\sum }_{i=1}^n{b}_i{x}_i{)}^2$ ，对 $998244353$ 取模.

\quad $1\le n\le 200,\sum n\le 10^4,det(A)\not\equiv 0(mod998244353)$.

二.分析

\quad 借鉴了这位大佬的讲解，下面只是转述一下.

\quad 此题为在满足一定约束条件下多元函数求最值问题，考虑使用拉格朗日乘数法.

\quad 做拉格朗日函数 $L(x_1,x_2,...,x_n,\lambda )={\sum }_{i=1}^n{b}_i{x}_i+\lambda ({\sum }_{i=1}^n{\sum }_{j=1}^n{A}_{i,j}{x}_i{x}_j-1)$.

\quad 对 $x_1,x_2,...,x_n,\lambda$ 分别求偏导并令其为 $0$，得到

\quad $\{\begin{array}{r}{b}_1+2\lambda \sum _{i=1}^n{A}_{1,i}{x}_i=0\\ b_2+2\lambda \sum _{i=1}^n{A}_{2,i}{x}_i=0\\ .......................\\ b_n+2\lambda \sum _{i=1}^n{A}_{n,i}{x}_i=0\\ \sum _{i=1}^n\sum _{j=1}^n{A}_{i,j}{x}_i{x}_j=1\end{array}⟹\{\begin{array}{r}b+2\lambda Ax=0①\\ x^{T}Ax=1②\end{array}$

\quad 由 ① 得 $x=-\frac{1}{2\lambda }{A}^{-1}b③$.

\quad 由 $x^{T}b=b^{T}x$ 并将 ③ 代入可得 $x^T=-\frac{1}{2\lambda }{b}^T{A}^{-1}④$.

\quad 将 ③，④ 代入 ② 整理可得 $\frac{1}{4{\lambda }^2}{b}^T{A}^{-1}b=1⑤$.

\quad 题目所求为 $({\sum }_{i=1}^n{b}_i{x}_i{)}^2$，即为 $(b^{T}x{)}^2$.

$\begin{array}{rl}(b^{T}x{)}^2& \stackrel{③}{=}(b^T\times (-\frac{1}{2\lambda }{A}^{-1}b){)}^2\\ & =\frac{1}{4{\lambda }^2}(b^T{A}^{-1}b)(b^T{A}^{-1}b)\\ & \stackrel{⑤}{=}{b}^T{A}^{-1}b\end{array}$

三.代码实现

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

const int M = (int)2e2;
const ll mod = (ll)998244353;

int n;

struct Matrix
{
    
    
    ll D[M + 5][M + 5];
}A, B, BT, AInv, C, ANS;

int is[M + 5], js[M + 5];

ll quick(ll a, ll b, ll p)
{
    
    
    ll s = 1;
    while(b)
    {
    
    
        if(b & 1) s = s * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return s;
}

ll inv(ll n, ll p)
{
    
    
    return quick(n, p - 2, p);
}

int Inv()
{
    
    
    for(int i = 1; i <= n; ++i) is[i] = js[i] = 0;
    for(int i = 1; i <= n; ++i) for(int j = 1; j <= n; ++j) AInv.D[i][j] = A.D[i][j];
    for(int k = 1; k <= n; ++k)
    {
    
    
        for(int i = k; i <= n; ++i)
        {
    
    
            for(int j = k; j <= n; ++j)
            {
    
    
                if(AInv.D[i][j])
                {
    
    
                    is[k] = i, js[k] = j;
                    break;
                }
            }
        }
        for(int i = 1; i <= n; ++i) swap(AInv.D[k][i], AInv.D[is[k]][i]);
        for(int i = 1; i <= n; ++i) swap(AInv.D[i][k], AInv.D[i][js[k]]);
        if(!AInv.D[k][k]) return -1;
        AInv.D[k][k] = inv(AInv.D[k][k], mod);
        for(int j = 1; j <= n; ++j) if(j != k) AInv.D[k][j] = AInv.D[k][j] * AInv.D[k][k] % mod;
        for(int i = 1; i <= n; ++i)
        {
    
    
            if(i != k)
            {
    
    
                ll tmp = AInv.D[i][k];
                AInv.D[i][k] = 0;
                for(int j = 1; j <= n; ++j) AInv.D[i][j] = ((AInv.D[i][j] - tmp * AInv.D[k][j] % mod) % mod + mod) % mod;
            }
        }
    }
    for(int k = n; k >= 1; --k)
    {
    
    
        for(int i = 1; i <= n; ++i) swap(AInv.D[js[k]][i], AInv.D[k][i]);
        for(int i = 1; i <= n; ++i) swap(AInv.D[i][is[k]], AInv.D[i][k]);
    }
    return 1;
}

void mul(const Matrix& A, int Ar, int Ac, const Matrix& B, int Br, int Bc, Matrix& C)
{
    
    
    for(int i = 1; i <= n; ++i) for(int j = 1; j <= n; ++j) C.D[i][j] = 0;
    for(int i = 1; i <= Ar; ++i)
    {
    
    
        for(int j = 1; j <= Bc; ++j)
        {
    
    
            for(int k = 1; k <= Ac; ++k)
            {
    
    
                C.D[i][j] = (C.D[i][j] + A.D[i][k] * B.D[k][j] % mod) % mod;
            }
        }
    }
}

char ch; int f; ll x;

ll read()
{
    
    
    x = 0, f = 1;
    ch = getchar();
    while(!isdigit(ch))
    {
    
    
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(isdigit(ch))
    {
    
    
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int main()
{
    
    
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    while(~scanf("%d", &n))
    {
    
    
        for(int i = 1; i <= n; ++i) for(int j = 1; j <= n; ++j) A.D[i][j] = (read() % mod + mod) % mod;
        for(int i = 1; i <= n; ++i) B.D[i][1] = (read() % mod + mod) % mod;
        for(int i = 1; i <= n; ++i) BT.D[1][i] = B.D[i][1];
        Inv();
        mul(BT, 1, n, AInv, n, n, C);
        mul(C, 1, n, B, n, 1, ANS);
        printf("%lld\n", (ANS.D[1][1] % mod + mod) % mod);
    }
    return 0;
}

F Infinite String Comparision

一.题目大意

\quad 对于字符串 $x$，定义 $x^{\infty }$ 为 $x$ 重复无限次的字符串

\quad 给定字符串 $a$ 和 $b$，求 $a^{\infty }$ 与 $b^{\infty }$ 字典序的相对大小（$1\le |a|,|b|\le 10^5$）

二.分析

\quad PPT题解是这么写的~~，说实话没看懂（周期引理怎么转化到这道题上的？有明白的大佬请留言）~~

Infinite String Comparision

• Compare the string a^{infty} and b^{infty} directly
• By the Periodicity Lemma, if there is no mismatches in the first a + b - gcd(a, b) characters, the two string are identical

\quad 其实直接比 $n+m$ 次就好啦~~，嗯，感觉是对的！~~

三.代码实现

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

const int M = (int)1e3;
const int inf = 0x3f3f3f3f;
const ll mod = (ll)998244353;
const double eps = 1e-8;

int n, m;
string s, t;

void work()
{
    
    
    n = s.size(), m = t.size();
    int cnt = n + m, i = 0, j = 0;
    while(cnt-- > 0)
    {
    
    
        if(s[i] < t[j]) {
    
    cout << "<" << endl; return;}
        else if(s[i] > t[j]) {
    
    cout << ">" << endl; return;}
        i = (i + 1) % n, j = (j + 1) % m;
    }
    cout << "=" << endl;
}

int main()
{
    
    
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    while(cin >> s >> t) work();
    return 0;
}

I 1 or 2

一.题目大意

\quad 给定 $n$ 个点，$m$ 条边的无向图和 $d[i]$ 数组。问是否能选出某些边使得 $i$ 号点的度为 $d[i]$，输出 “Yes” 或 “No”.

二.分析

\quad 按照度 $d[i]$ 拆点，之后再拆边，跑一般图最大匹配看是否为完美匹配.

\quad 用下面这个数据举例

4 4
1 2 1 0
1 2
1 4
2 3
3 4

\quad 那么拆点、拆边后的图变为

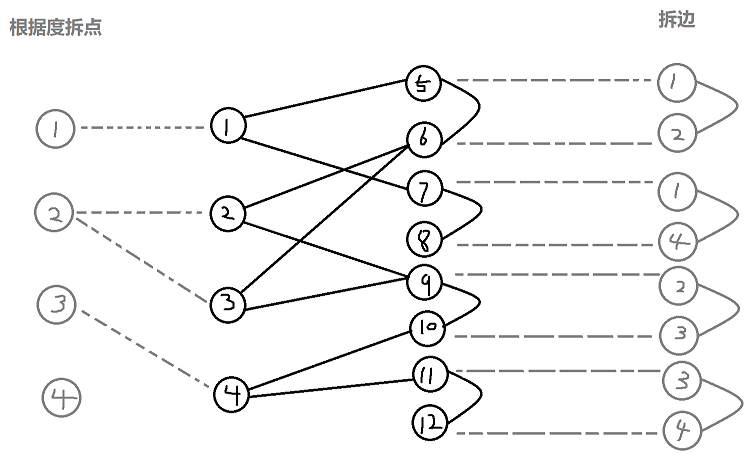
\quad 在黑图上跑一般图最大匹配，结果如下图所示，其中红边为匹配边

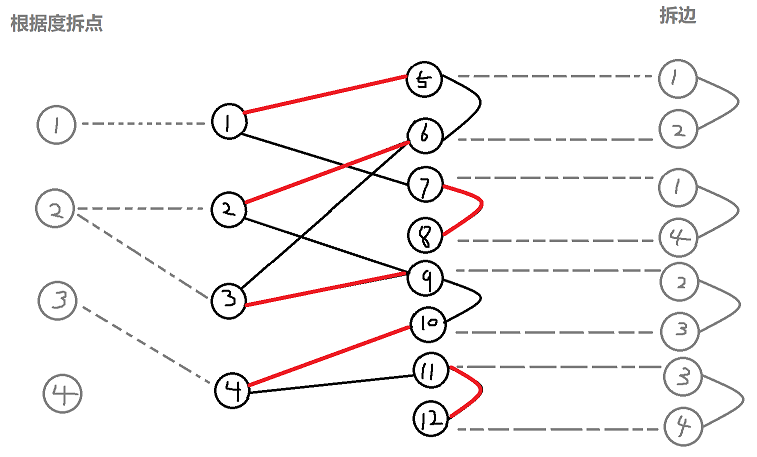
\quad 最后如果为完美匹配，则输出"Yes"，否则为"No".

\quad 思考一下这样为什么是对的？

\quad 因为如果黑图中存在完美匹配，则说明每个点的每个度都与且仅与一条边相应的端点相连，满足题目要求。拆点得到的点与拆边得到的点之前的红线表示相应灰边对相应灰点的度的贡献为1，拆边得到的点与拆边得到的点之前的红线则表示相应灰边对灰点的度的贡献为0，可以删去；反之同理。

三.代码实现

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

const int M = (int)3e2;
const int N = (int)1e3;
const int inf = 0x3f3f3f3f;
const ll mod = (ll)998244353;
const double eps = 1e-8;

int n, m, cnt;
int head[M + 5];
struct enode
{
    
    
    int v, nx;
}Edge[N + 5];

void init()
{
    
    
    cnt = 0;
    for(int i = 1; i <= n; ++i)
    {
    
    
        head[i] = -1;
    }
}

void add(int u, int v)
{
    
    
    Edge[cnt].v = v;
    Edge[cnt].nx = head[u];
    head[u] = cnt++;
}

struct MP
{
    
    
    int ma[M + 5], st[M + 5], pr[M + 5], fa[M + 5], q[M + 5], v[M + 5];
    int ti, u, t;

    void init()
    {
    
    
        ti = u = t = 0;
        for(int i = 0; i <= n; ++i)
        {
    
    
            ma[i] = st[i] = pr[i] = fa[i] = q[i] = v[i] = 0;
        }
    }

    int lca(int x, int y)
    {
    
    
        for(ti++; ; swap(x, y))
        {
    
    
            if(!x) continue;
            if(v[x] == ti) return x;
            v[x] = ti;
            x = fa[pr[ma[x]]];
        }
    }

    void up(int x, int y, int f)
    {
    
    
        while(fa[x] != f)
        {
    
    
            pr[x] = y;
            if(st[ma[x]] > 0) st[q[++t] = ma[x]] = 0;
            if(fa[x] == x) fa[x] = f;
            if(fa[ma[x]] == ma[x]) fa[ma[x]] = f;
            x = pr[y = ma[x]];
        }
    }

    int match(int x)
    {
    
    
        for(int i = 1; i <= n; ++i) fa[i] = i, st[i] = -1;
        st[q[t = 1] = x] = 0;
        for(int l = 1, v; l <= t; ++l)
        {
    
    
            for(int i = head[q[l]]; ~i; i = Edge[i].nx)
            {
    
    
                v = Edge[i].v;
                if(st[v] < 0)
                {
    
    
                    st[v] = 1;
                    pr[v] = q[l];
                    if(!ma[v])
                    {
    
    
                        for(int j = q[l], k = v; j; j = pr[k = u])
                        {
    
    
                            u = ma[j];
                            ma[j] = k;
                            ma[k] = j;
                        }
                        return 1;
                    }
                    st[q[++t] = ma[v]] = 0;
                }
                else if(fa[v] != fa[q[l]] && !st[v])
                {
    
    
                    int f = lca(v, q[l]);
                    up(q[l], v, f); up(v, q[l], f);
                    for(int j = 1; j <= n; ++j) fa[j] = fa[fa[j]];
                }
            }
        }
        return 0;
    }

    int solve()
    {
    
    
        int ans = 0;
        for(int i = 1; i <= n; ++i) ans += !ma[i] && match(i);
        return ans;
        /* ans为一般图最大匹配点对数
        ma[i]为i号点对应的匹配点，0表示未匹配*/
    }
}mp;

int nn;
vector <int> de[M + 5];

int main()
{
    
    
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    while(~scanf("%d %d", &n, &m))
    {
    
    
        nn = 0;
        for(int i = 1, d; i <= n; ++i)
        {
    
    
            scanf("%d", &d);
            de[i].clear();
            while(d--) de[i].push_back(++nn);
        }
        n = nn + 2 * m;
        init();
        for(int i = 1, u, v; i <= m; ++i)
        {
    
    
            scanf("%d %d", &u, &v);
            add(nn + 1, nn + 2), add(nn + 2, nn + 1);
            ++nn; for(auto x: de[u]) add(x, nn), add(nn, x);
            ++nn; for(auto x: de[v]) add(x, nn), add(nn, x);
        }
        mp.init();
        int ans = mp.solve();
        puts(ans * 2 == n ? "Yes" : "No");
    }
    return 0;
}

J Easy Integration

一.题目大意

\quad $10^5$次查询${\int }_0^1(x-x^2{)}^{n}dx$，$1\le n\le 10^6$.

二.分析

$\begin{array}{rl}{\int }_0^1{x}^n(1-x{)}^{n}dx& ={\int }_0^1{x}^n(1-x{)}^{n}dx\\ & =\frac{1}{n+1}{\int }_0^1(1-x{)}^{n}d{x}^{n+1}=\frac{n}{n+1}{\int }_0^1{x}^{n+1}(1-x{)}^{n-1}dx\\ & =\frac{n}{(n+1)(n+2)}{\int }_0^1(1-x{)}^{n}d{x}^{n+2}=\frac{n(n-1)}{(n+1)(n+2)}{\int }_0^1{x}^{n+2}(1-x{)}^{n-2}dx\\ & \stackrel{迭代}{=}\frac{(n)(n-1)...(1)}{(n+1)(n+2)...(2n)}{\int }_0^1{x}^{2n}dx\\ & =\frac{(n)(n-1)...(1)}{(n+1)(n+2)...(2n)(2n+1)}\\ & =\frac{(n!{)}^2}{(2n+1)!}\end{array}$

三.代码实现

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;

const int M = (int)2e6 + 1;
const int inf = 0x3f3f3f3f;
const ll mod = (ll)998244353;
const double eps = 1e-8;

ll fac[M + 5];

ll quick(ll a, ll b, ll p)
{
    
    
    ll s = 1;
    while(b)
    {
    
    
        if(b & 1) s = s * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return s;
}

ll inv(ll n, ll p)
{
    
    
    return quick(n, p - 2, p);
}

int main()
{
    
    
//    freopen("input.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
    fac[0] = 1; for(int i = 1; i <= M; ++i) fac[i] = fac[i - 1] * i % mod;
    int n;
    while(~scanf("%d", &n))
    {
    
    
        ll s = 1;
        s = s * fac[n] % mod * fac[n] % mod;
        s = s * inv(fac[2 * n + 1], mod) % mod;
        printf("%lld\n", s);
    }
    return 0;
}