从零手写VIO的第五次作业总结

文章目录

基础作业
提升作业

作业题目：

基础作业

MakeHessian()

海塞矩阵计算原理

在这里插入图片描述
分析：

这里残差的信息矩阵 $\varSigma$ ,使用的是一个2×2的单位矩阵,在edge.cc文件里有定义

    Eigen::MatrixXd information(residual_dimension, residual_dimension);
    information.setIdentity();
    information_ = information;

代码

void Problem::MakeHessian() {
    
    
    TicToc t_h;
    // 直接构造大的 H 矩阵
    ulong size = ordering_generic_;
    MatXX H(MatXX::Zero(size, size));
    VecX b(VecX::Zero(size));
    // 遍历所有残差
    for (auto &edge: edges_) {
    
    

        edge.second->ComputeResidual(); // r
        edge.second->ComputeJacobians();// j

        auto jacobians = edge.second->Jacobians();  // 该边的雅克比
        auto verticies = edge.second->Verticies();  // 该边的三个顶点
        assert(jacobians.size() == verticies.size());
        for (size_t i = 0; i < verticies.size(); ++i) {
    
    
            auto v_i = verticies[i];
            if (v_i->IsFixed()) continue;    // Hessian 里不需要添加它的信息，也就是它的雅克比为 0

            auto jacobian_i = jacobians[i];
            ulong index_i = v_i->OrderingId();  // 该边的顶点v_i在H中的Orderingid 表示在H中的位置
            ulong dim_i = v_i->LocalDimension();

            MatXX JtW = jacobian_i.transpose() * edge.second->Information();    // JT*Σ-1
            for (size_t j = i; j < verticies.size(); ++j) {
    
    
                auto v_j = verticies[j];

                if (v_j->IsFixed()) continue;

                auto jacobian_j = jacobians[j];
                ulong index_j = v_j->OrderingId();
                ulong dim_j = v_j->LocalDimension();

                assert(v_j->OrderingId() != -1);
                MatXX hessian = JtW * jacobian_j;
                // 所有的信息矩阵叠加起来
                // TODO:: home work. 完成 H index 的填写.
                // H.block(?,?, ?, ?).noalias() += hessian;
                H.block(index_i,index_j, dim_i,dim_j).noalias()+=hessian;
                if (j != i) {
    
    
                    // 对称的下三角
                    // TODO:: home work. 完成 H index 的填写.
                    // H.block(?,?, ?, ?).noalias() += hessian.transpose();
                    H.block(index_j,index_i, dim_j,dim_i).noalias()+=hessian.transpose();
                }
            }
            // b
            b.segment(index_i, dim_i).noalias() -= JtW * edge.second->Residual();
        }

    }
    Hessian_ = H;
    b_ = b;
    t_hessian_cost_ += t_h.toc();


//    Eigen::JacobiSVD<Eigen::MatrixXd> svd(H, Eigen::ComputeThinU | Eigen::ComputeThinV);
//    std::cout << svd.singularValues() <<std::endl;

    if (err_prior_.rows() > 0) {
    
    
        b_prior_ -= H_prior_ * delta_x_.head(ordering_poses_);   // update the error_prior
    }
    Hessian_.topLeftCorner(ordering_poses_, ordering_poses_) += H_prior_;
    b_.head(ordering_poses_) += b_prior_;

    delta_x_ = VecX::Zero(size);  // initial delta_x = 0_n;

}

H矩阵分析
对于雅克比 $J_i$ ,其 $H$ 如下图所示

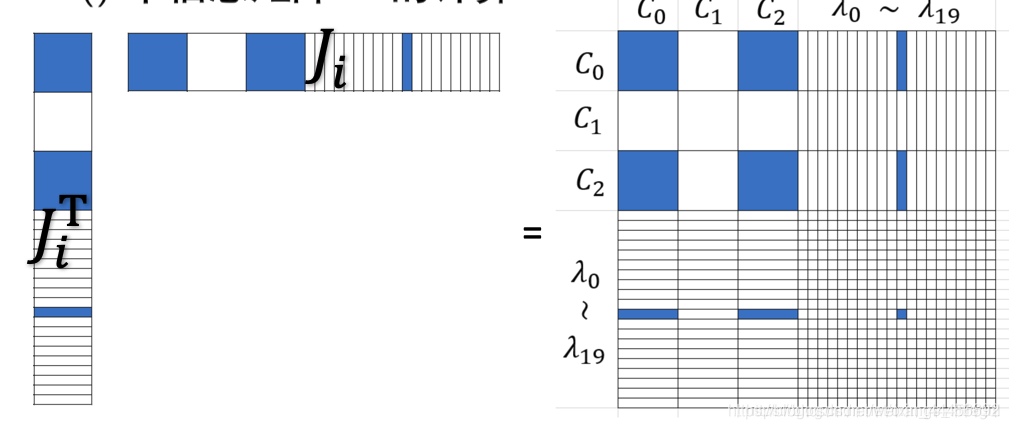
图片参考：https://blog.csdn.net/orange_littlegirl/article/details/103369583#t1

将40个edge所对应的40个 $H_{38×38}$ 连加即可得到总的信息矩阵H。
在这里插入图片描述

SolveLinearSystem()

舒尔补解加速解方程原理

在这里插入图片描述

计算分析

在这里插入图片描述

代码

void Problem::SolveLinearSystem() {
    
    

    if (problemType_ == ProblemType::GENERIC_PROBLEM) {
    
    

        // 非 SLAM 问题直接求解
        // PCG solver
        MatXX H = Hessian_;
        for (ulong i = 0; i < Hessian_.cols(); ++i) {
    
    
            H(i, i) += currentLambda_;
        }
//        delta_x_ = PCGSolver(H, b_, H.rows() * 2);
        delta_x_ = Hessian_.inverse() * b_;

    } else {
    
    

        // SLAM 问题采用舒尔补的计算方式
        // step1: schur marginalization --> Hpp, bpp
        int reserve_size = ordering_poses_;
        int marg_size = ordering_landmarks_;
        MatXX Hmm = Hessian_.block(reserve_size,reserve_size, marg_size, marg_size);
        MatXX Hpm = Hessian_.block(0,reserve_size, reserve_size, marg_size);
        MatXX Hmp = Hessian_.block(reserve_size,0, marg_size, reserve_size);
        VecX bpp = b_.segment(0,reserve_size);
        VecX bmm = b_.segment(reserve_size,marg_size);

        // Hmm 是对角线矩阵，它的求逆可以直接为对角线块分别求逆，如果是逆深度，对角线块为1维的，则直接为对角线的倒数，这里可以加速
        MatXX Hmm_inv(MatXX::Zero(marg_size, marg_size));
        for (auto landmarkVertex : idx_landmark_vertices_) {
    
    
            int idx = landmarkVertex.second->OrderingId() - reserve_size;
            int size = landmarkVertex.second->LocalDimension();
            Hmm_inv.block(idx, idx, size, size) = Hmm.block(idx, idx, size, size).inverse();
        }

        // TODO:: home work. 完成舒尔补 Hpp, bpp 代码
        MatXX Hpp = Hessian_.block(0,0,reserve_size,reserve_size);
        MatXX tempH = Hpm * Hmm_inv;
        H_pp_schur_ = Hpp - tempH * Hmp;
        b_pp_schur_ = bpp - tempH * bmm;

        // step2: solve Hpp * delta_x = bpp
        VecX delta_x_pp(VecX::Zero(reserve_size));
        // PCG Solver
        for (ulong i = 0; i < ordering_poses_; ++i) {
    
    
            H_pp_schur_(i, i) += currentLambda_;
        }

        int n = H_pp_schur_.rows() * 2;                       // 迭代次数
        delta_x_pp = PCGSolver(H_pp_schur_, b_pp_schur_, n);  // 哈哈，小规模问题，搞 pcg 花里胡哨
        delta_x_.head(reserve_size) = delta_x_pp;
        //        std::cout << delta_x_pp.transpose() << std::endl;

        // TODO:: home work. step3: solve landmark
        VecX delta_x_ll(marg_size);
        // delta_x_ll = ???;
        delta_x_ll = Hmm_inv * (bmm- Hmp*delta_x_pp);   //Hmp*delta_x_pp + Hmm*delata_x_ll = bmm
        delta_x_.tail(marg_size) = delta_x_ll;      // 至此我们解出delta_x_ = [delata_x_pp; delata_x_ll]

    }

}

程序执行结果：
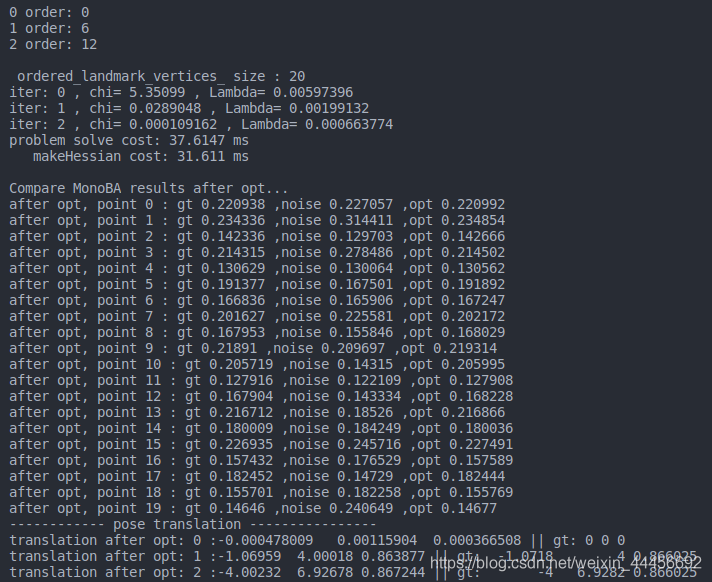
在这里插入图片描述
可以看到，相机位姿和空间点的逆深度估计的都比较好

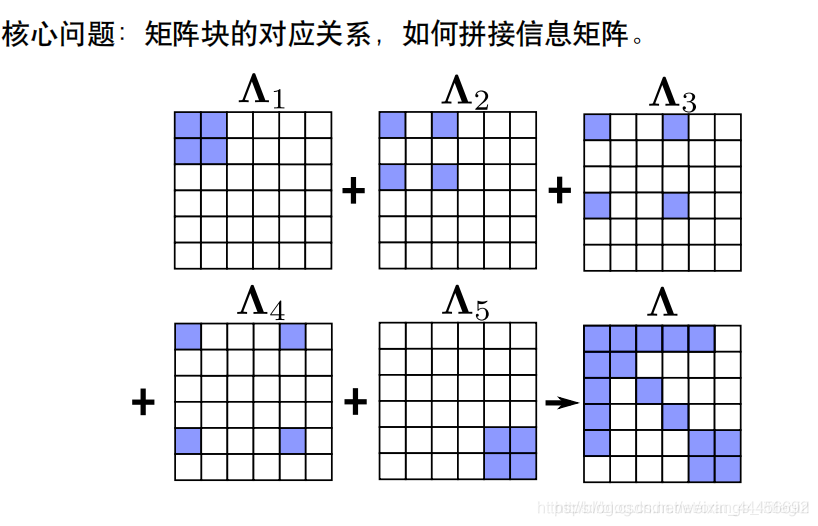
TestMarginalize()

滑动窗口算法原理

案例：
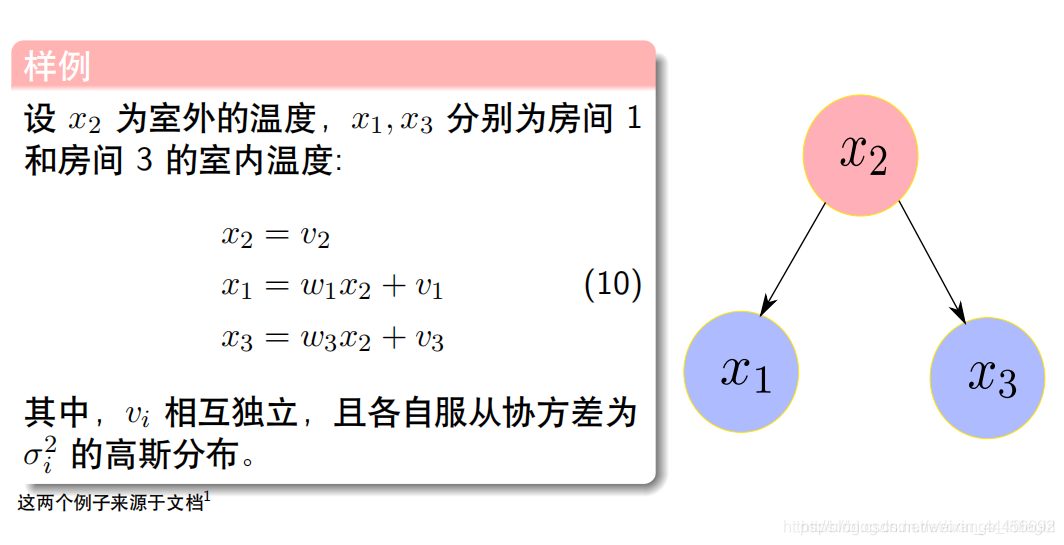
信息矩阵

对应代码

 	double delta1 = 0.1 * 0.1;
    double delta2 = 0.2 * 0.2;
    double delta3 = 0.3 * 0.3;

    int cols = 3;
    MatXX H_marg(MatXX::Zero(cols, cols));
    H_marg << 1./delta1, -1./delta1, 0,
            -1./delta1, 1./delta1 + 1./delta2 + 1./delta3, -1./delta3,
            0.,  -1./delta3, 1/delta3;

求解思路

首先将 $x_2$ 在信息矩阵的位置移动到右下角,信息矩阵利用交换法则
然后利用舒尔补marg掉Amm, H_prior = Arr - Arm * Amm_inv * Amr
$\Lambda = \Lambda_{\alpha \alpha}-\Lambda_{\alpha \beta}\Lambda_{\beta \beta}^{-1}\Lambda_{\beta \alpha}$

代码

void Problem::TestMarginalize() {
    
    

    // Add marg test
    int idx = 1;            // marg 中间那个变量
    int dim = 1;            // marg 变量的维度
    int reserve_size = 3;   // 总共变量的维度
    double delta1 = 0.1 * 0.1;
    double delta2 = 0.2 * 0.2;
    double delta3 = 0.3 * 0.3;

    int cols = 3;
    MatXX H_marg(MatXX::Zero(cols, cols));
    H_marg << 1./delta1, -1./delta1, 0,
            -1./delta1, 1./delta1 + 1./delta2 + 1./delta3, -1./delta3,
            0.,  -1./delta3, 1/delta3;
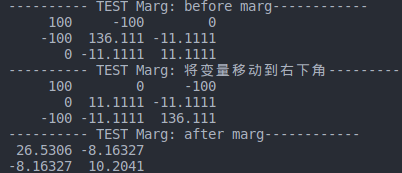
    std::cout << "---------- TEST Marg: before marg------------"<< std::endl;
    std::cout << H_marg << std::endl;

    // TODO:: home work. 将变量移动到右下角
    /// 准备工作： move the marg pose to the Hmm bottown right
    // 将 row i 移动矩阵最下面 也就是将第2行和第3行交换
    Eigen::MatrixXd temp_rows = H_marg.block(idx, 0, dim, reserve_size);
    Eigen::MatrixXd temp_botRows = H_marg.block(idx + dim, 0, reserve_size - idx - dim, reserve_size);
    // H_marg.block(?,?,?,?) = temp_botRows;
    // H_marg.block(?,?,?,?) = temp_rows;
    H_marg.block(idx, 0, reserve_size - idx - dim, reserve_size) = temp_botRows;
    H_marg.block(reserve_size - dim, 0, dim, reserve_size) = temp_rows;


    // 将 col i 移动矩阵最右边 也就是将第二列和第三列交换
    Eigen::MatrixXd temp_cols = H_marg.block(0, idx, reserve_size, dim);
    Eigen::MatrixXd temp_rightCols = H_marg.block(0, idx + dim, reserve_size, reserve_size - idx - dim);
    H_marg.block(0, idx, reserve_size, reserve_size - idx - dim) = temp_rightCols;
    H_marg.block(0, reserve_size - dim, reserve_size, dim) = temp_cols;

    std::cout << "---------- TEST Marg: 将变量移动到右下角------------"<< std::endl;
    std::cout<< H_marg <<std::endl;

    /// 开始 marg ： schur
    double eps = 1e-8;
    int m2 = dim;
    int n2 = reserve_size - dim;   // 剩余变量的维度
    Eigen::MatrixXd Amm = 0.5 * (H_marg.block(n2, n2, m2, m2) + H_marg.block(n2, n2, m2, m2).transpose());

    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);
    Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd(
            (saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() *
                              saes.eigenvectors().transpose();

    // TODO:: home work. 完成舒尔补操作
    //Eigen::MatrixXd Arm = H_marg.block(?,?,?,?);
    //Eigen::MatrixXd Amr = H_marg.block(?,?,?,?);
    //Eigen::MatrixXd Arr = H_marg.block(?,?,?,?);
    Eigen::MatrixXd Arm = H_marg.block(0, n2, n2, m2);
    Eigen::MatrixXd Amr = H_marg.block(n2, 0, m2, n2);
    Eigen::MatrixXd Arr = H_marg.block(0, 0, n2, n2);


    Eigen::MatrixXd tempB = Arm * Amm_inv;
    Eigen::MatrixXd H_prior = Arr - tempB * Amr;

    std::cout << "---------- TEST Marg: after marg------------"<< std::endl;
    std::cout << H_prior << std::endl;
}

程序执行结果：

提升作业

整理中……

参考：手写VIO学习总结（五）

从零手写VIO(五)