文章目录

章节安排
- 1. 数学基础部分（1~6）
- 2. SLAM技术部分（7~14）
第一讲前言和简介
第二讲初识SLAM
第三讲三维空间刚体运动
第四讲李群和李代数
第五讲相机与图像

章节安排

1. 数学基础部分（1~6）

第一讲介绍这本书的基本信息，习题部分主要包括一些自测题。
第二讲为 SLAM 系统概述，介绍一个 SLAM 系统由哪些模块组成，各模块的具体工作是什么。实践部分介绍编程环境的搭建过程以及 IDE 的使用。
第三讲介绍三维空间运动，接触旋转矩阵、四元数、欧拉角的相关知识，并且在 Eigen 当中使用它们。
第四讲为李群和李代数。学习李代数的定义和使用方式，然后通过 Sophus 操作它们。
第五讲介绍针孔相机模型以及图像在计算机中的表达。用 OpenCV 来调取相机的内外参数。
第六讲介绍非线性优化，包括状态估计理论基础、最小二乘问题、梯度下降方法。完成一个使用 Ceres 和 g2o 进行曲线拟合的实验。

2. SLAM技术部分（7~14）

第七讲为特征点法的视觉里程计。该讲内容比较多，包括特征点的提取与匹配、对极几何约束的计算、PnP 和 ICP 等。在实践中，用这些方法去估计两个图像之间的运动。
第八讲为直接法的视觉里程计。学习光流和直接法的原理，然后利用 g2o实现一个简单的 RGB-D 直接法。
第九讲为视觉里程计的实践章，将搭建一个视觉里程计框架，综合应用先前学过的知识，实现它的基本功能。从中会碰到一些问题，例如优化的必要性、关键帧的选择等。
第十讲为后端优化，主要为 Bundle Adjustment 的深入讨论，包括基本的 BA以及如何利用稀疏性加速求解过程。将用 Ceres 和 g2o 分别书写一个 BA 程序。
第十一讲主要讲后端优化中的位姿图。位姿图是表达关键帧之间约束的一种更紧凑的形式。将用 g2o 和 gtsam 对一个位姿球进行优化。
第十二讲为回环检测，主要介绍以词袋方法为主的回环检测。使用dbow3 书写字典训练程序和回环检测程序。
第十三讲为地图构建。我们会讨论如何使用单目进行稠密深度图的估计（以及这是多么不可靠），然后讨论 RGB-D 的稠密地图构建过程。书写极线搜索与块匹配的程序，然后在 RGB-D 中遇到点云地图和八叉树地图的构建问题。
第十四讲主要介绍当前的开源 SLAM 项目以及未来的发展方向。

第一讲前言和简介

什么是SLAM：
SLAM 是 Simultaneous Localization and Mapping 的缩写，中文译作“同时定位与地图构建”。它是指搭载特定传感器的主体，在没有环境先验信息的情况下，于运动过程中建立环境的模型，同时估计自己的运动。

第二讲初识SLAM

相机：

以二维投影形式记录三维世界的信息
丢掉了一个维度——距离

三种视觉SLAM中主要的相机：

单目相机：没有深度，必须通过移动相机产生深度（近处物体的像运动快，远处物体的像运动慢）
双目相机：通过两个眼睛的视差计算深度（近处物体差别大，远处物体差别小），计算量很大
RGBD相机：通过物理方法测量深度，知道每个点的深度
主动测量，功耗很大
结构光TOF
深度值比较准确
量程小，易受干扰（很多RGBD用的是红外光，会受太阳光干扰，因此室外还是要用单目和双目，RGBD不太行）

视觉SLAM框架

传感器信息读取：在视觉 SLAM 中主要为相机图像信息的读取和预处理。如果在机器人中,还可能有码盘、惯性传感器等信息的读取和同步。
视觉里程计 (Visual Odometry, VO)：视觉里程计任务是估算相邻图像间相机的运动,以及局部地图的样子。VO 又称为前端(Front End)。
分为基于特征点法的视觉里程计（第七讲）和基于直接法的视觉里程计（第八讲）
后端非线性优化（Optimization）：后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对他们进行优化，得到全局一致的地图。由于在VO之后，又被称为后端（Back End）
（只要前端里有误差的东西，都可以放到后端进行优化）
主流方式：前期是以滤波器为代表的滤波的方法（EKF），现在是以图优化为代表的优化的方法
第六讲整体介绍，第十讲和第十一讲详细介绍图优化、捆集调整、位姿图
回环检测（Loop Closure Detection）：回环检测机器人是否到达过先前的位置，如果检测到回环，它会把信息提供给后端进行处理。
主流方法：词袋模型（十二讲）
建图（mapping）：它根据估计的轨迹，建立与任务要求对应的地图
（十三讲）

SLAM问题的数学描述

运动方程：

通常，机器人会携带一个测量自身运动的传感器，比如说码盘或惯性传感器。这个传感器可以测量有关运动的读数，但不一定直接是位置之差，还可能是加速度、角速度等信息
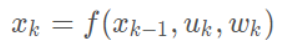
在这里插入图片描述
其中Xk是当前位置，Xk-1是上一时刻位置，uk是输入，wk是噪声
运动方程只有在带有运动传感器的时候才存在
观测方程：
观测方程描述的是，当小萝卜在 xk 位置上看到某个路标点 yj，产生了一个观测数据 zk,j
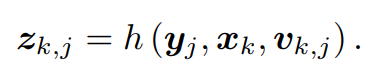
在这里插入图片描述
观测方程的数量是不一定的，取决于xk那个时刻看到了多少个路标y

cmake

CmakeList.txt

常用框架如下
目录结构如下：
├── test目录
│ ├── CMakeLists.txt
│ ├── bin目录(存放生成的可执行文件)
│ ├── include目录
│ │ ├── file1.h
│ ├── src 目录
│ │ ├── main.cpp
│ │ ├── file1.cpp
│ ├── build目录

# 声明要求的 cmake 最低版本
#这行命令是可选的，我们可以不写这句话，但在有些情况下，如果 CMakeLists.txt 文件中使用了一些高版本 cmake 特有的一些命令的时候，就需要加上这样一行，提醒用户升级到该版本之后再执行 cmake。
cmake_minimum_required( VERSION 2.8 )

# 声明一个 cmake 工程名称
project( 01 )

# 设置编译模式，可以选择Debug或者Release
set( CMAKE_BUILD_TYPE "Debug" )
set(CMAKE_CXX_FLAGS_DEBUG "$ENV{CXXFLAGS} -O0 -Wall -g2 -ggdb")
set(CMAKE_CXX_FLAGS_RELEASE "$ENV{CXXFLAGS} -O3 -Wall")

# 添加一个可执行程序
# 语法：add_executable( 程序名 源代码文件 ）
add_executable( main src/main.cpp )
#将可执行文件输出到文件夹bin中，方便管理
set(EXECUTABLE_OUTPUT_PATH  ${
    
    PROJECT_SOURCE_DIR}/bin)

# 包含头文件所在目录
include_directories(${
    
    PROJECT_SOURCE_DIR}/include)

# 添加一个库，默认为静态链接库
# add_library( namesp src/namesp.cpp )
# 添加一个动态共享库
add_library( file1_shared SHARED src/file1.cpp )

# 将库文件链接到可执行程序上
target_link_libraries( main file1_shared )

其他

在写.h文件的时候，可以使用编译预处理指令#pragma once代替ifndef #define，他们的效果是一样的，但是更简洁

使用#progma once
#pragma once  
// Code placed here is included only once per translation unit 

使用宏定义方式
#ifndef HEADER_H_ 
#define HEADER_H_  
// Code placed here is included only once per translation unit  
#endif // HEADER_H_

第三讲三维空间刚体运动

本讲主要介绍：一个刚体在三维空间中的运动是如何描述的
- 理论部分：介绍旋转矩阵、四元数、欧拉角的意义，以及它们是如何运算和转换的
- 实践部分：将介绍线性代数库 Eigen。它提供了 C++ 中的矩阵运算，并且它的 Geometry 模块还提供了四元数等刚体运动的描述。

3.1 旋转矩阵

向量的运算

对于向量a,b
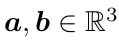
在这里插入图片描述

内积：

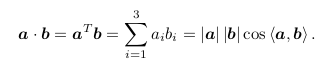
内积可以描述向量间的投影关系
外积

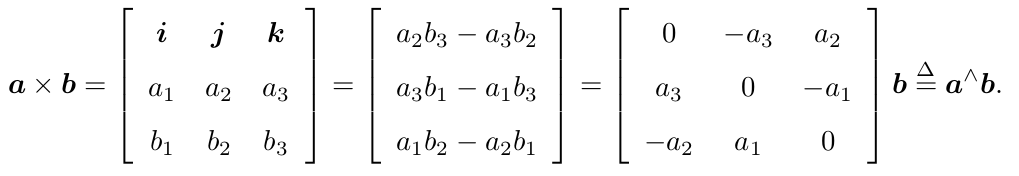
外积的方向垂直于这两个向量,大小为 |a| |b| sin ⟨a, b⟩,是两个向量张成的四边形的有向面积.
我们引入了^符号,把 a 写成一个矩阵.这样就把外积 a × b,写成了矩阵与向量的乘法 a ∧ b,把它变成了线性运算.
注意：外积只对三维向量存在定义,我们还能用外积表示向量的旋转

欧式变换

欧氏变换：相机运动是一个刚体运动，它保证了同一个向量在各个坐标系下的长度和夹角都不会发生变化。这种变换称为欧氏变换
旋转矩阵：
旋转矩阵R的充要条件：
①R是一个正交阵，矩阵的逆和转置相等
②|R| = 1

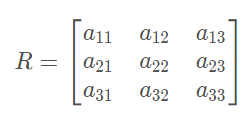
3.2 齐次坐标和变换矩阵

齐次坐标：我们把一个三维向量的末尾添加 1，变成了四维向量，称为齐次坐标。对于这个四维向量，我们可以把旋转和平移写在一个矩阵里面，使得整个关系变成了线性关系。
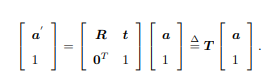
变换矩阵：上式中的T称为变换矩阵

3.3 旋转向量和欧拉角

旋转向量

使用矩阵方式(旋转矩阵和变换矩阵)表示三维刚体运动的缺陷：

SO(3) 的旋转矩阵有九个量，但一次旋转只有三个自由度。因此这种表达方式是冗余的。同理，变换矩阵用十六个量表达了六自由度的变换。
旋转矩阵自身带有约束：它必须是个正交矩阵，且行列式为 1。变换矩阵也是如此。当我们想要估计或优化一个旋转矩阵/变换矩阵时，这些约束会使得求解变得更困难。

旋转向量：任意旋转都可以用一个旋转轴和一个旋转角来刻画。于是，我们可以使用一个向量，其方向与旋转轴一致，而长度等于旋转角。这种向量，称为旋转向量。

罗德里格斯公式:
罗德里格斯公式实现了从旋转向量到旋转矩阵的转换
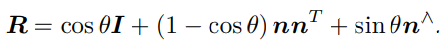
在这里插入图片描述

欧拉角

它使用了三个分离的转角，把一个旋转分解成三次绕不同轴的旋转。
欧拉角当中比较常用的一种，是用“偏航-俯仰-滚转”（yaw-pitch-roll）三个角度来描述一个旋转。
欧拉角存在“万向锁”问题：在俯仰角为±90◦ 时，第一次旋转与第三次旋转将使用同一个轴，使得系统丢失了一个自由度。

四元数

旋转矩阵用九个量描述三自由度的旋转，具有冗余性；欧拉角和旋转向量是紧凑的，但具有奇异性。
引入一种和数学中复数类似的数，
数学中的复数：乘上复数 i 相当于逆时针把一个复向量旋转 90 度。
四元数正是在表达三维空间旋转时的一种类似的代数

优点：它既是紧凑的，也没有奇异性。
缺点：四元数不够直观，运算较为复杂

定义：

一个四元数 q 拥有一个实部和三个虚部。

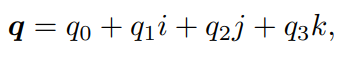
其中 i, j, k 为四元数的三个虚部。这三个虚部满足关系式：

由于它的这种特殊表示形式，有时人们也用一个标量和一个向量来表达四元数：

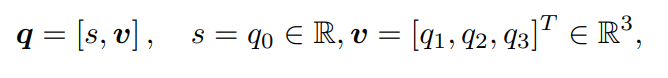
这里，s 称为四元数的实部，而 v 称为它的虚部。如果一个四元数虚部为 0，称之为实四元数。反之，若它的实部为 0，称之为虚四元数。

3.4 Eigen库

环境需求

Eigen库的安装
使用以下命令

sudo apt-get install libeigen3-dev

在CmakeLists里包含eigen头文件
添加下面这一行，(一般来说路径都是这个)

include_directories( "/usr/include/eigen3" )

在cpp文件里包含头文件

// Eigen 部分
#include <Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>

基本语法

#include <iostream>
using namespace std;
#include <ctime>//包含计时的函数，在本程序中用来对比两种方程求解方法的运算速度
// Eigen 部分
#include <Eigen/Core>
// 稠密矩阵的代数运算（逆，特征值等）
#include <Eigen/Dense>

#define MATRIX_SIZE 50

/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/

int main( int argc, char** argv )
{
    
    
    // Eigen 中所有向量和矩阵都是Eigen::Matrix，它是一个模板类。它的前三个参数为：数据类型，行，列
    // 声明一个2*3的float矩阵
    Eigen::Matrix<float, 2, 3> matrix_23;
    // 同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Eigen::Matrix
    // 例如 Vector3d 实质上是 Eigen::Matrix<double, 3, 1>，即三维向量
    Eigen::Vector3d v_3d;
	// 这是一样的
    Eigen::Matrix<float,3,1> vd_3d;
    // Matrix3d 实质上是 Eigen::Matrix<double, 3, 3>
    Eigen::Matrix3d matrix_33 = Eigen::Matrix3d::Zero(); //初始化为零
    // 如果不确定矩阵大小，可以使用动态大小的矩阵
    Eigen::Matrix< double, Eigen::Dynamic, Eigen::Dynamic > matrix_dynamic;
    // 更简单的
    Eigen::MatrixXd matrix_x;
    // 这种类型还有很多，我们不一一列举

    // 下面是对Eigen阵的操作
    // 输入数据（初始化）
    matrix_23 << 1, 2, 3, 4, 5, 6;
    // 输出
    cout << matrix_23 << endl;

    // 用()访问矩阵中的元素
    for (int i=0; i<2; i++) {
    
    
        for (int j=0; j<3; j++)
            cout<<matrix_23(i,j)<<"\t";
        cout<<endl;
    }

    // 矩阵和向量相乘（实际上仍是矩阵和矩阵）
    v_3d << 3, 2, 1;
    vd_3d << 4,5,6;
    // 但是在Eigen里你不能混合两种不同类型的矩阵，像这样是错的
    // Eigen::Matrix<double, 2, 1> result_wrong_type = matrix_23 * v_3d;
    // 应该显式转换
    Eigen::Matrix<double, 2, 1> result = matrix_23.cast<double>() * v_3d;
    cout << result << endl;

    Eigen::Matrix<float, 2, 1> result2 = matrix_23 * vd_3d;
    cout << result2 << endl;

    // 同样你不能搞错矩阵的维度
    // 试着取消下面的注释，看看Eigen会报什么错
    // Eigen::Matrix<double, 2, 3> result_wrong_dimension = matrix_23.cast<double>() * v_3d;

    // 一些矩阵运算
    // 四则运算就不演示了，直接用+-*/即可。
    matrix_33 = Eigen::Matrix3d::Random();      // 随机数矩阵
    cout << matrix_33 << endl << endl;

    cout << matrix_33.transpose() << endl;      // 转置
    cout << matrix_33.sum() << endl;            // 各元素和
    cout << matrix_33.trace() << endl;          // 迹
    cout << 10*matrix_33 << endl;               // 数乘
    cout << matrix_33.inverse() << endl;        // 逆
    cout << matrix_33.determinant() << endl;    // 行列式

    // 特征值
    // 实对称矩阵可以保证对角化成功
    Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> eigen_solver ( matrix_33.transpose()*matrix_33 );
    cout << "Eigen values = \n" << eigen_solver.eigenvalues() << endl;
    cout << "Eigen vectors = \n" << eigen_solver.eigenvectors() << endl;
    // 解方程
    // 我们求解 matrix_NN * x = v_Nd 这个方程
    // N的大小在前边的宏里定义，它由随机数生成
    // 直接求逆自然是最直接的，但是求逆运算量大

    Eigen::Matrix< double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
    matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
    Eigen::Matrix< double, MATRIX_SIZE,  1> v_Nd;
    v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );

    clock_t time_stt = clock(); // 计时
    // 直接求逆
    Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;
    cout <<"time use in normal inverse is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;
    
	// 通常用矩阵分解来求，例如QR分解，速度会快很多
    time_stt = clock();
    x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
    cout <<"time use in Qr decomposition is " <<1000*  (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;

    return 0;
}

第四讲李群和李代数

群

群的定义
群（Group）是一种集合加上一种运算的代数结构。我们把集合记作 A，运算记作 ·，那么群可以记作 G = (A, ·)。群要求这个运算满足以下几个条件：
1.封闭性: ∀a1, a2 ∈ A, a1 · a2 ∈ A.
2.结合律: ∀a1, a2, a3 ∈ A, (a1 · a2) · a3 = a1 · (a2 · a3).
3.幺元: ∃a0 ∈ A, s.t. ∀a ∈ A, a0 · a = a · a0 = a.
4.逆: ∀a ∈ A, ∃a⁻¹ ∈ A, s.t. a · a⁻¹ = a0.
群的例子：
实数关于加法是一个群，封闭性和结合律不必说，这个群的幺元是0，逆就是数a的相反数。
常见的群
一般线性群 GL(n) 指 n × n 的可逆矩阵，它们对矩阵乘法成群。
特殊正交群 SO(n) 也就是所谓的旋转矩阵群，其中 SO(2) 和SO(3) 最为常见。
特殊欧氏群 SE(n) 也就是前面提到的 n 维欧氏变换，如 SE(2) 和 SE(3)。

李群

李群
李群是指具有连续（光滑）性质的群。
像整数群 Z 那样离散的群没有连续性质，所以不是李群。而 SO(n) 和 SE(n)，它们在实数空间上是连续的。
李群的例子
三维旋转矩阵构成了特殊正交群 SO(3)，而变换矩阵构成了特殊欧氏群 SE(3)

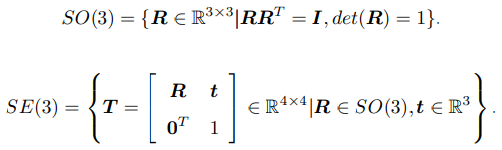
李代数

李代数
每个李群都有与之对应的李代数。李代数描述了李群的局部性质。通用的李代数的定义如下：
李代数由一个集合 V，一个数域 F 和一个二元运算 [, ] 组成。如果它们满足以下几条性质，称 (V, F, [ , ]) 为一个李代数，记作 g。
1.封闭性： ∀X,Y ∈ V, [X,Y ] ∈ V.
2.双线性： ∀X,Y , Z ∈ V, a, b ∈ F, 有：[aX + bY , Z] = a[X, Z] + b[Y , Z], [Z, aX + bY ] = a[Z, X] + b[Z,Y ].
3.自反性： ∀X ∈ V, [X, X] = 0.
4.雅可比等价： ∀X,Y , Z ∈ V, [X, [Y , Z]] + [Z, [Y , X]] + [Y , [Z, X]] = 0.

其中的二元运算被称为李括号。李括号表达了两个元素的差异。
李代数的例子：三维向量 R³ 上定义的叉积 × 是一种李括号，因此 g = (R³, R, ×) 构成了一个李代数。

李代数so(3)

李代数so(3)是定义在R³上的三维向量，记作 ϕ
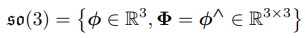
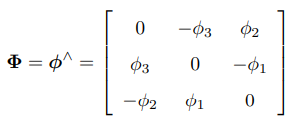
李代数so(3)的李括号为
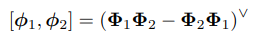
李群SO(3)与李代数so(3)的映射关系为指数映射

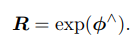
李代数se(3)

与so(3)类似，se(3)是定义在R⁶空间上的六维向量，记作ξ。
它的前三维为平移，记作 ρ；后三维为旋转，记作 ϕ，实质上是 so(3) 元素。
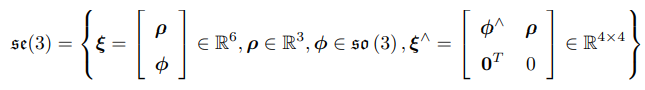
李代数的上尖∧
在 se(3) 中，同样使用 ∧ 符号，将一个六维向量转换成四维矩阵，但这里不再表示反对称.
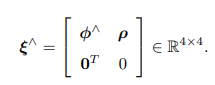
李代数的李括号

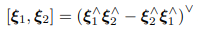
其中下尖∨与上尖∧相反，表示“从矩阵到向量”的关系

指数与对数映射

SO(3)和so(3)

从so(3)到SO(3)的指数映射
ϕ 是三维向量，我们可以定义它的模长和它的方向，分别记作 θ 和 a，于是有 ϕ = θa，则从so(3)到SO(3)的指数映射可以表示为：

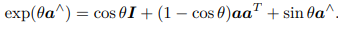
这个式子是不是看起来很眼熟，没错它就是我们在上一章学过的罗德里格斯公式
从SO(3)到so(3)的对数映射
按照定义可以写出如下的映射关系(但通常我们不这么算)

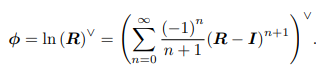
通常我们用上一章中讲过的这种计算方式

SE(3)和se(3)

从se(3)到SE(3)的指数映射

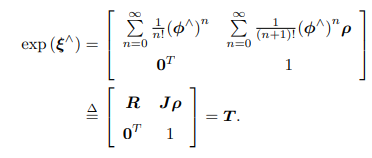
其中

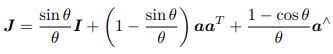
我们看到，平移部分经过指数映射之后，发生了一次以 J 为系数矩阵的线性变换
从SE(3)到se(3)的指数映射
ξ=ln(T) ^∨
根据变换矩阵 T 求 so(3) 上的对应向量也有更省事的方式：从左上的 R 计算旋转向量，而右上的 t 满足：t = Jρ
由于 J 可以由 ϕ 得到，所以这里的 ρ 亦可由此线性方程解得。

SO(3), SE(3), so(3), se(3) 的对应关系

在这里插入图片描述

李代数求导与扰动模型

BCH 公式与近似形式

BCH公式
注意，对于矩阵，以下这个式子并不成立

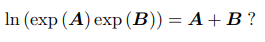
两个李代数指数映射乘积的完整形式，由 Baker-Campbell-Hausdorff 公式（BCH 公式）给出。由于它完整的形式较复杂，我们给出它展开式的前几项

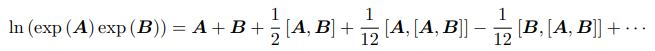
其中 [,] 为李括号。
SO(3)上的近似形式

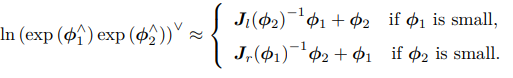
当ϕ1为小量时称为左乘，ϕ2为小量时称为右乘
左乘 BCH 近似雅可比 J_l：

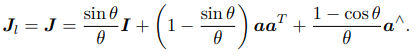
它的逆为

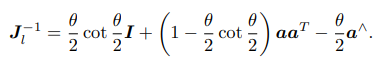
右乘雅可比J_r仅需要对自变量取负号即可
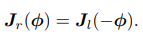
SE(3)上的近似形式

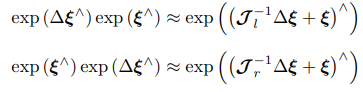
BCH近似的意义

假定对某个旋转 R，对应的李代数为 ϕ。我们给它左乘一个微小旋转，记作 ∆R，对应的李代数为 ∆ϕ。那么，在李群上，得到的结果就是 ∆R · R，而在李代数上，根据 BCH近似，为：J_l^-1(ϕ)∆ϕ + ϕ。合并起来，可以简单地写成：
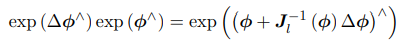
在这里插入图片描述
反之在李代数上进行加法：

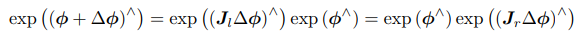
SO(3) 李代数上的求导

有两种模型，导数模型和扰动模型

导数模型：用李代数表示姿态，然后对根据李代数加法来对李代数求导。
扰动模型：对李群左乘或右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。

假设我们对一个空间点 p 进行了旋转，得到了 Rp

导数模型
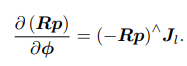
扰动模型(左乘为例)

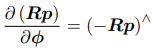
SE(3)上的李代数求导(扰动模型)

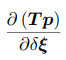
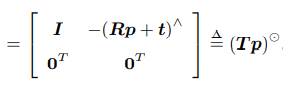
在这里插入图片描述

第五讲相机与图像

5.1 针孔相机模型

5.1.1 推导过程

在这里插入图片描述

O − x − y − z 为相机坐标系；实际物体点P在相机坐标系中的坐标为[X,Y,Z]^T，投影到O’-X’-Y’平面上的点P’坐标为[X’,Y’,Z’]^T，则有
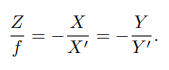
我们把像投影到前方（这样可以去掉负号）

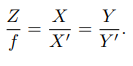
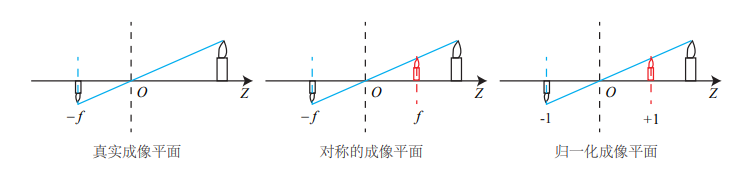
整理得
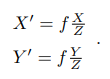
相机坐标系到像素坐标系
设像素坐标为[u,v]^T

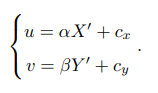
进一步地

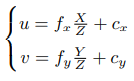
最终得到

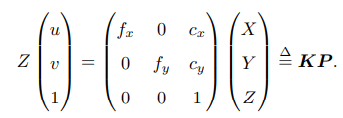
其中K称为内参数矩阵
内参：通常认为，相机的内参在出厂之后是固定的，不会在使用过程中发生变化，我们把它看做相机的固有属性，所以称为内参。
将相机坐标P转换为世界坐标P_W

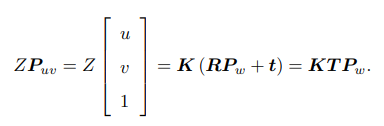
其中T称为外参数矩阵
注意：上式隐含了一次从齐次坐标到非齐次坐标的转换(KTP_W是一个41的，而等号左边是31的)
P点的归一化处理
将P点归一化到Z=1的归一化平面上，的到归一化坐标P_C

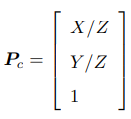
5.1.2 参和外参的含义

内参矩阵K表示了从归一化的相机坐标到像素坐标的变换
外参矩阵T（或R,t）表示了从世界坐标到相机坐标的变换

5.2 相机的畸变

畸变通常包含两种：径向畸变和切向畸变

5.2.1 径向畸变

来源
由透镜形状引起的畸变称之为径向畸变
主要类型
主要包括，桶形畸变和枕形畸变

桶形畸变是由于图像放大率随着离光轴的距离增加而减小，而枕形畸变却恰好相反。
在这两种畸变中，穿过图像中心和光轴有交点的直线还能保持形状不变。
矫正公式

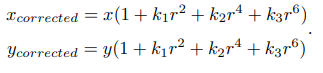
本公式都是指归一化平面上的点，其中 r 表示点 p 离坐标系原点的距离

5.2.2 切向畸变

来源
切向畸变来源于透镜和成像面不平行
矫正公式

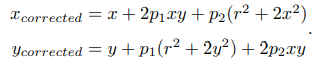
本公式都是指归一化平面上的点，其中 r 表示点 p 离坐标系原点的距离，θ 表示和水平轴的夹角

5.2.3 畸变的矫正

将三维空间点投影到归一化图像平面。设它的归一化坐标为 [x, y]^T
对归一化平面上的点进行径向畸变和切向畸变纠正
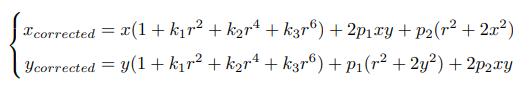
将纠正后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置

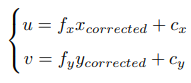
5.3 单目相机成像过程

首先，世界坐标系下有一个固定的点 P，世界坐标为 P_W；
由于相机在运动，它的运动由 R, t 或变换矩阵 T ∈ SE(3) 描述。P 的相机坐标为：P˜_c = RP_W + t。
（这里应该是P_c头顶上有个波浪，但是笔者太菜，打不出来，大家知道就好）
这时的 P˜_c仍有 X, Y, Z 三个量，把它们投影到归一化平面 Z = 1 上，得到 P 的归一化相机坐标：P_c = [X/Z, Y /Z, 1]^T
最后，P 的归一化坐标经过内参后，对应到它的像素坐标：P_uv = KP_c

5.4 双目相机

双目相机成像模型

O_L, O_R为左右光圈中心，蓝色框为成像平面，f 为焦距。u_L 和 u_R 为成像平面的坐标。请注意按照图中坐标定义，u_R 应该是负数，所以图中标出的距离为 −u_R。
距离计算公式

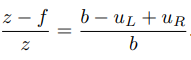
整理得

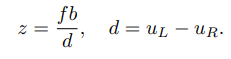
这里 d 为左右图的横坐标之差，称为视差（Disparity）
双目相机量程
由于视差最小为一个像素，于是双目的深度存在一个理论上的最大值，由 fb 确定。因此通常来说想要测的远，相机就会更大

5.5 RGBD相机

目前的 RGB-D 相机按原理可分为两大类：

通过红外结构光（Structured Light）来测量像素距离的。例子有 Kinect 1 代、ProjectTango 1 代、Intel RealSense 等；
通过飞行时间法（Time-of-flight, ToF）原理测量像素距离的。例子有 Kinect 2 代和一些现有的 ToF 传感器等。

本讲当中还有关于图像的基本知识和OpenCV的相关知识，可以参见笔者另一篇文章OpenCV相关知识.

视觉SLAM十四讲笔记

文章目录

章节安排

1. 数学基础部分（1~6）

2. SLAM技术部分（7~14）

第一讲 前言和简介

第二讲 初识SLAM

相机：

视觉SLAM框架

SLAM问题的数学描述

cmake

CmakeList.txt

其他

第三讲 三维空间刚体运动

3.1 旋转矩阵

向量的运算

欧式变换

3.2 齐次坐标和变换矩阵

3.3 旋转向量和欧拉角

旋转向量

欧拉角

四元数

3.4 Eigen库

环境需求

基本语法

第四讲 李群和李代数

群

李群

李代数

李代数so(3)

李代数se(3)

指数与对数映射

SO(3)和so(3)

SE(3)和se(3)

SO(3), SE(3), so(3), se(3) 的对应关系

李代数求导与扰动模型

BCH 公式与近似形式

BCH近似的意义

SO(3) 李代数上的求导

SE(3)上的李代数求导(扰动模型)

第五讲 相机与图像

5.1 针孔相机模型

5.1.1 推导过程

5.1.2 参和外参的含义

5.2 相机的畸变

5.2.1 径向畸变

5.2.2 切向畸变

5.2.3 畸变的矫正

5.3 单目相机成像过程

5.4 双目相机

5.5 RGBD相机

猜你喜欢

第一讲前言和简介

第二讲初识SLAM

第三讲三维空间刚体运动

第四讲李群和李代数

第五讲相机与图像