[4G&5G专题-33]：物理层-浅谈ZC序列的原理以及在LTE PSS中的应用

第1章 ZC序列概述

1.1序列的定义

1.2 复指数回顾

2.3 把ZC符号序列，映射到PSS的子载波上（调制）

2.4 ZC符号的相位调制与普通相位调制的比较

第1章 ZC序列概述

1.1序列的定义

数学上，序列是被排成一列的对象（或事件）；

每个元素不是在其他元素之前，就是在其他元素之后。

如果排列的对象是二进制比特0或1，称为二进制序列。二进制序列是坐标轴上的0和1两个点组成的序列，不同点可以重叠。

如果排列的对象是整数，那么称为整数序列。整数序列是横或纵坐标轴上的一个个的点组成的序列，点可以重叠。

如果排列的对象是复数，那么称为复数序列。复数序列是平面坐标中的一个个的点组成的序列，点可以重叠。

1.2 复指数回顾

（1）复数的极坐标形式

$a+bi=rcos\theta +irsin\theta=r(cos\theta +isin\theta )=re^{i\theta }$
r：模 $\theta$ ：幅角

（2）欧拉公式

$e^{i\theta }=cos\theta +isin\theta$
输入的是实数 $\theta$ ，输出的是复数，它的一般形式是 $u(\theta )+iv(\theta )$ ，这种函数叫实变量复（数）值函数。

欧拉函数首先是一个复数函数；其次，实部和虚部满足一定的关系，即平方和等于1。

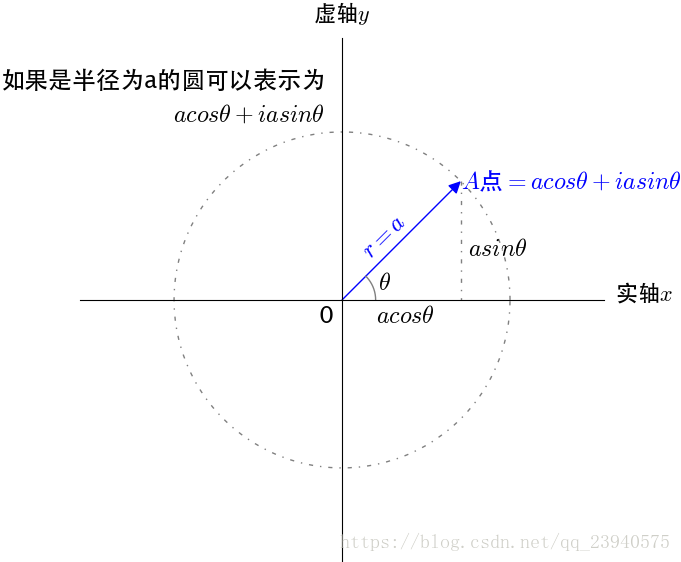
欧拉序列：是有单位圆上的一个个点组成的、特殊的、复数序列。

1.3 ZC序列概述

在4G LTE系统中，PSS、SSS、cellRS、DMRS、SRS、PRACH、PUCCH等物理层信号，基本上都涉及到了ZC（Zadoff –Chu）序列信号。

在5G NR系统中，除了采用M序列来生成抵抗大频偏场景的PSS和SSS信号，其它信号也同样涉及到了Zadoff –Chu序列。

Zadoff –Chu序列，顾名思义，就是Zadoff 和Chu共同发现的序列。

ZC序列并不是一个二进制序列，而是一个欧拉复数序列。

也就是说，ZC序列并不是横坐标或纵坐标上一个个点的序列，也不是平面坐标上的任意一个个点的序列，而是复平面坐标上的单位圆上的一个个点组成的序列。

1.5 ZC序列的数学公式

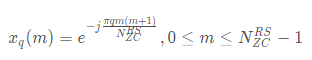
其中m是序列的序号，q和N都是可调参数，则圆上的点与坐标轴的夹角为：

$\phi = \frac{\pi * q*m(m+1) }{N}$

在q和N确定的情况下, ZC序列的点如下图所示：

1.6 ZC序列与复指数相位调制的关系

如果把ZC序列的一个个点，作为复指数信号的调制信号，就会得到相位调制的信号。

载波信号：任意频率的复指数信号

调制信号的幅度A：恒定不变, 落在单位元上。

调制信号的相位：满足 $\phi = \frac{\pi * q*m(m+1) }{N}$

1.7 ZC序列的特点

（1）恒包络

任意长度的ZC序列的信号的幅值是恒定的，这也意味着功率恒定，这个好处就是射频器件不用忽大忽小的改变能量。

（2）理想周期自相关

（3）良好的互相关

ZC序列循环移位N后，原序列只与移位后的序列得良好的相关峰值，其它位置的序列相关峰值为0。

除此之外，两个根如果是互质的，生成的序列相关峰值几乎为零。

（4）傅立叶变换后仍是ZC序列

这个性质，简直就是为OFDM系统量身打造，也省去多少运算量。既可以在时域相关，也可以在频域相关，灵活决定姿势，怎么方便怎么来。

在这里插入图片描述

OFDM符号采用IFFT变换而来，OFDM符号要想保持正交性，就要求首尾要保持相位的连续性。

OFDM本质是多个并行的子载波采用正交IQ调制，然后相加在一起，以单个子载波对应的时间周期T，离散化后，刚好是一个离散逆傅立叶变换IFFT，这是OFDM调制采用IFFT变换的本质。

（5）对于发端，ZC序列峰均比低（ZC序列时频域都是ZC序列，且幅值恒定），有利于射频功放信号发挥最大的效率。

（6）对于信道估计，ZC序列幅值恒定，其图形可看作一个单位圆。

第2章 PSS ZC序列的产生过程

2.1 ZC符号的产生

（1）设定PSS中的小区ID为0,1,2

（2）0,1,2映射到ZC序列函数中的参数root index上，在上图中，体现公式中的q或u参数上。

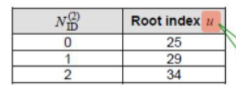
（3）设定PSS ZC序列的个数62，即n=0,1,2,3，......61

（4）设定PSS ZC序列的参数N=63, 使之满足0<= n <= N-1

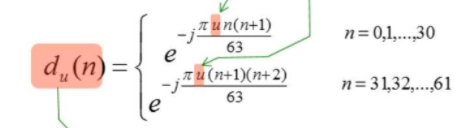
（5）取u=25，n=0,1,2,3，......61，得到NID=0时，由62个单位圆上的点组成的ZC序列。

这个序列实际上是单位圆上的一个个点，相位满足： $\phi = \frac{\pi * 25 *n(n+1) }{63}$

（5）取u=29, n=0,1,2,3，......61，得到NID=1时，由62个单位圆上的点组成的ZC序列。

这个序列实际上是单位圆上的一个个点，相位满足： $\phi = \frac{\pi * 29 *n(n+1) }{63}$

（5）取u=34, n=0,1,2,3，......61，得到NID=2时，由62个单位圆上的点组成的ZC序列。

这个序列实际上是单位圆上的一个个点，相位满足： $\phi = \frac{\pi * 34 *n(n+1) }{63}$

至此，根据不同的物理小区ID号，得到3组不同的ZC序列。实际上，一个确定的小区，其小区ID是确定的，因此其ZC序列也是确定的。

PSS是一个ZC序列，由62个符号组成。NCellID不同时，PSS序列也是不同的，这表示PSS序列随NCellID (PCI: Physical CellID)变化而变化。

2.2 PSS的子载波

PSS和SSS信号位于小区中心频点的72个子载波上，即中心的6个RB上。

其中，不包含中心频点DC（DC其实也占用了一个Sc，因此对于更底层来说准确的应该是73）。

2.3 把ZC符号序列，映射到PSS的子载波上（调制）

PSS的ZC序列，由62个符号构成。PSS的子载波有72个，足以承载62个符号。

实际只使用了频率中心DC周围的62个子载波，两边各留了5个（5+5=10）子载波用作保护波段。

也就是说，用于承载ZC序列的子载波的个数只需要62个。

因此PSS的ZC序列与PSS的子载波是一一对应的关系。

$^{_{}}$ $\large ^{a_{k,l}}$ 中的k表示：在时频矩阵中的子载波编号，l表示：时频矩阵中的时间轴的编号，即符号数。

表示小区中心频点处的子载波号。

上述公式，实际就是把PSS的ZC序列按顺序一一映射到PSS的一个个子载波。

2.4 ZC符号的相位调制与普通相位调制的比较

把ZC符号序列，映射到PSS的子载波上的过程实际上是一个相位调制PSK的过程。

与普通相位调制相比，有相同点，也有不同点：

（1）相同点：

不改变载波的幅度
不改变载波的频率
调制的是载波的相位
都是复指数调制和IQ调制
复指数调制和IQ调制的本质是通过幅度控制相位

（2）不同点：

相位的可变性：普通的相位调制的相位值是固定几种，如45°，90°，135°等等，而ZC的相位值可以是任意的。
相位的数量：普通的相位调制的相位的数量是固定，如QPSK是4种，8PSK为8种，而ZC的相位远远大于这个，PSS ZC序列的相位就有62个。

2.5 ZC序列的本质

经过如上的阐述，可以看出，ZC序列实际上是有无数个不同相位序列构成的子载波序列！！！

第3章 UE对PSS ZC序列的检测过程

（1）UE会在其支持的LTE频率的中心频点附近去尝试接收PSS和SSS。

（2）UE并不需要解调出每个子载波的相位值，只需要得到复指数的幅度值就可以了。

（3）UE也不需要先算出Root Index，在计算得到对应的NID.

（3）由于UE是知道PSS ZC序列的格式的，因此UE可以预先生产ZC序列的复指数信号的幅度值序列，然后用幅度值序列与收到的信号的幅度序列进行匹配，即模式匹配。

（4）因此UE获取NID的方法是采用模式匹配。

第4章复指数回顾

4.1 复数的定义

复数变实数，需要用到共轭性质： $z=a+bi$ ， $\overline{z}=a-bi$ ， $z\overline{z}=(a+bi)(a-bi)=a^{2}+b^{2}$

4.2 复数的计算

分子分母同乘以分母的共轭复数

$\frac{2+i}{1-3i}\times \frac{1+3i}{1+3i}=\frac{-1+7i}{10}=-\frac{1}{10}+\frac{7}{10}i$

4.3 复数的极坐标形式

$a+bi=rcos\theta +irsin\theta=r(cos\theta +isin\theta )=re^{i\theta }$
r：模 $\theta$ ：幅角

4.4 欧拉公式

$e^{i\theta }=cos\theta +isin\theta$
输入的是实数 $\theta$ ，输出的是复数，它的一般形式是 $u(\theta )+iv(\theta )$ ，这种函数叫实变量复（数）值函数。

4.5 指数函数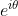 $e^{i\theta }$ 的性质：

指数函数的运算法则（指数率）： $e^{i\theta_{1} }\cdot e^{i\theta_{2} } =e^{i(\theta_{1}+\theta_{2}) }$ ，或者 $(cos\theta_{1}} +isin\theta_{1})(cos\theta_{2}} +isin\theta_{2})=cos(\theta_{1}+\theta_{2})+isin(\theta_{1}+\theta_{2})$ ；
$e^{i\theta }$ 的求导法则： $({e^{i\theta }})'=ie^{i\theta }$ ，或者 ${(cos\theta +isin\theta)}'= {cos\theta}'+i{sin\theta}'=-sin\theta +icos\theta =i(cos\theta +isin\theta)$
当 $\theta=0$ 时： $e^{i0}=1$ ，或者 $cos0 +isin0=1+0=1$
这个定义符合无穷级数

4.6 两个复数相乘：

用极坐标算，只需将模r相乘，幅角 $\theta$ 相加： $r_{1}e^{i\theta_{1} }\cdot r_{2}e^{i\theta_{2} }=r_{1}r_{2}e^{i(\theta_{1} +\theta_{2} )}$
用直角坐标算会很麻烦： $(a_{1}+b_{1}i)(a_{2}+b_{2}i)=......$

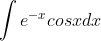4.7 求积分 $\int e^{-x}cosxdx$ ：

直接算可以用分部积分法，但很麻烦
因为 $cosx$ 是 $e^{ix}$ 的实数部分，所以可以将 $e^{ix}$ 替换 $cosx$ ，原方程变为 $\int e^{-x}e^{ix}dx$ ，积分完成后再去掉虚数部分即可
$\int e^{-x}e^{ix}dx=\int e^{(-1+i)x}dx=\frac{e^{(-1+i)x}}{-1+i}\cdot \frac{-1-i}{-1-i} =\frac{1}{2}e^{-x}e^{ix}(-1-i)$
将 $e^{ix}$ 转换成三角函数： $\frac{1}{2}e^{-x}e^{ix}(-1-i)=\frac{1}{2}e^{-x}(cosx+isinx)(-1-i)$
去掉虚数部分得： $\frac{1}{2}e^{-x}(-cosx+sinx)$

4.8 计算 $\sqrt[n]{1}$ ：

在实数范围内，计算结果只有：1或±1
在复数范围内，计算结果有n个：单位圆上的n个等分点（ $e^{i\theta_{1} }$ ， $e^{i\theta_{2} }$ ，……， $e^{i\theta_{n} }$ ）
证明：因为是单位圆，模相乘r=1；因为是等分点，幅角相加 $\theta _{1}+\theta _{2}+......\theta _{n}=2\pi =0$ ， $e^{i0}=1$
几何图见视频40:00~45:00