上个博客说道动态规划的引入,今天看一下动态规划的一个分支,01背包;
01背包问题
为什么,要叫他01背包呢,顾名思义,他的状态只有0或者1两种状态;也就是,拿与不拿;
国际惯例,用一道题来说明;
洛谷P1048----采药

现在他需要知道,到底采哪种药,会使得价值最高;
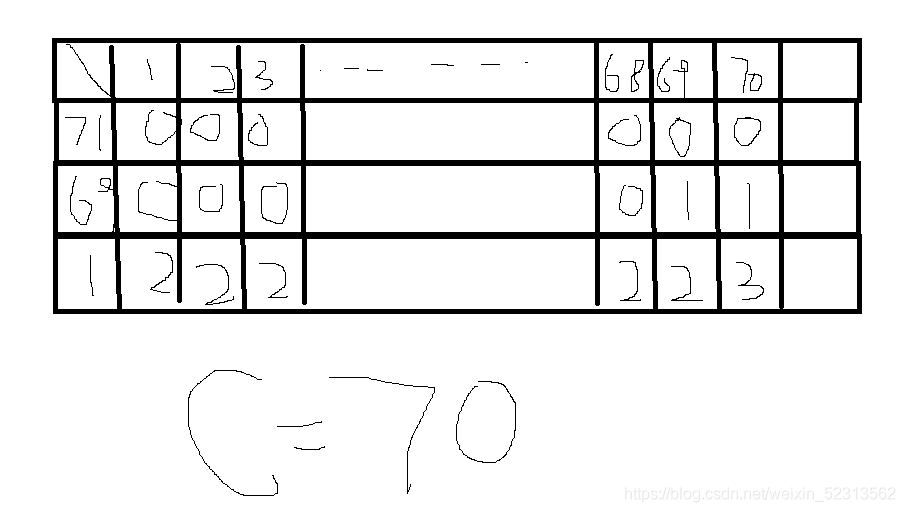
假设,我们现在按照题目的样例来想;

现在我们可用的时间是70;左边这一列表示不同药采的时间,上边这一行表示背包大小;
首先第一行,由于71>70所以说,不管哪个状态下,我们采药的价值都是0;

接着看第二行,刚开始的时候,背包重量从1,开始加,所以,当背包大小小于69时,背包容量不够,放不下药,当背包大于等于69是,采药所产生的价值为1;

再看下一行,当背包重量是1的时候,采药可以产生的最大价值为2;之后一直向后递推

这时,当背包大小为69的时候,我们有两种选择,一个是拿1不拿69,一个是拿69不拿1;显然,拿1的价值更大;
当背包为70的时候,我们既可以拿1也可以拿69,此时最大价值就是3;

所以说,对于一件物品,我们可以选择拿或者不拿,来确定其自身价值,我们用一个二维数组dp来表示;
用w[i]表示每个物品重量,v[i]表示物品价值;
int dp[i][j] 表示对于第i个物品,背包大小为j的时候的最大价值;
此时对于i来说,如果此时背包大小够装下这个物品 (j>=w[i]) ,那么此时
dp[i]j[j]就是上一个物品时候 (dp[i-1][j]) 的状态加上这个物品的价值v[i],与此同时,背包的大小也要减小w[i] (dp[i-1][j-w[i]]) ;
即,dp[i][j]=max{dp[i-1][j-w[i]]+v[i],dp[i-1][j]}
如果此时背包大小装不下这个物品,那么dp[i][j]=dp[i-1][j];
主要的核心代码就是:
for (int i = 1; i <= m; i++)
for (int j = t; j >= 0; j--)
{
if (j >= w[i])
{
dp[i][j] = max(dp[i - 1][j - w[i]] + v[i], dp[i - 1][j]);
}
else
{
dp[i][j] = dp[i - 1][j];
}
}
这个题的完整源码如下;
#include<iostream>
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
int dp[105][1005];
int w[105], v[105];
int main()
{
int m,t;
cin >> t >> m;
for (int i = 1; i <= m; i++)
{
cin >> w[i]>> v[i];
}
for (int i = 1; i <= m; i++)
for (int j = t; j >= 0; j--)
{
if (j >= w[i])
{
dp[i][j] = max(dp[i - 1][j - w[i]] + v[i], dp[i - 1][j]);
}
else
{
dp[i][j] = dp[i - 1][j];
}
}
cout << dp[m][t];
return 0;
}
再看一道洛谷的01背包变形版;
这个题与上面不同的就是,他状态有赢有输,而赢和输都会增加经验值;
所以这个的状态转移方程就变成了;
dp[j]=max(dp[j-use[i]]+win[i],dp[j]+lose[i]);
完整代码如下;
#include<bits/stdc++.h>
using namespace std;
long long use[1005],win[1005],lose[1005];
long long dp[1005];
int main()
{
long long n,x;
cin>>n>>x;
for(int i=1;i<=n;i++)
{
cin>>lose[i]>>win[i]>>use[i];
}
for(int i=1;i<=n;i++)
{
for(int j=x;j>=0;j--)
{
if(j>=use[i])
{
dp[j]=max(dp[j-use[i]]+win[i],dp[j]+lose[i]);
}
else
{
dp[j]=dp[j]+lose[i];
}
}
}
cout<<dp[x]*5;
return 0;
}
01背包的优化;
上面说到01背包需要一个二维数组来记录对应的状态,但是二维数组很容易就是出现MLE;
所以就有了,一维数组的01背包;
从上面我们能看出dp[i]完全是由dp[i-1】递推出来的;
所以我们只需要用一个dp[j]的一维数组,通过每次更新最大价值来完成这个题;
具体代码如下:
for(int i=1;i<=m;i++)
{
for(int j=t;j>=0;j--)
{
if(j>=w[i])
{
dp[j]=max(dp[j-w[i]]+v[i], dp[j]);
}
}
这样子大大减小了内存占用率;
完全背包
完全背包与01背包不同的是;01背包只有拿与不拿,而完全背包却是可以一直拿,
所以,他的核心代码相对于01背包就有了一点变换化
for(int i = 1;i <= m;i ++){
for(int j = w[i];j <= T;j ++){
f[j] = max(dp[j],dp[j - w[i]] + v[i]);
}
例如下面这个题,就可以完全套用这个模板
#include<iostream>
#include<algorithm>
using namespace std;
const int maxm = 10010, maxt = 10000010;
long long v[maxm], t[maxm], f[maxt];
int main(){
int T , m;
cin >> T >> m;
for(int i = 1;i <= m ;i ++) cin >> t[i] >> v[i];
for(int i = 1;i <= m;i ++){
for(int j = t[i];j <= T;j ++){
f[j] = max(f[j],f[j - t[i]] + v[i]);
}
}
cout << f[T];
}