这两天学习了01背包与完全背包,经过无数次百度之后,总算明白了一些其中的原理,记录一下。
01背包问题:
描述:假设小偷去珠宝店盗窃,他的背包容量为C=10,珠宝店里有3件珠宝可以盗窃,他们分别对应:

问可以装入背包的最大价值是多少。
求解:
想要求装入背包的最大价值,肯定要在尽量装满背包的情况下拿价值尽可能高的物品,使得最后的总价值最大化。这便要求局部最优解,分解子问题,自然而然需要用到动态规划。我们用dp[N][M]来定义面对N件物品剩余空间为M时的最优解,space[i]与val[i]分别代表占的空间与价值,第i件物品是否可以拿,存在两种情况:
(1)剩余空间不能装下此物品,那么问题转化为将前i-1件物品放入背包中所获得的最大价值。
(2)剩余空间可以装下此物品,想要求i件物品最优解,对于此物品又面临拿与不拿两种情况:
a.拿走此物品,此时的价值就应该是(i-1)件物品时的最优解加上此物品的价值。相应的,因为拿走了这件物品,空间也会对应减少,此时的状态即:dp[i-1][j-space[i]]+val[i]
b.不拿此物品,此时的价值就应该与拿走前(i-1)件物品获得的最大价值相同,虽然没有拿走这个物品,但是空间也没有减少,这意味着剩下的空间还可以装别的东西。此时的状态即:dp[i-1][j];
根据以上两种情况,我们不难得出状态转移方程:
if(j<space[i])
dp[i][j]=dp[i-1][j];
else
dp[i][j]=max(dp[i-1][j],dp[i-1][j-space[i]]+val[i]);最初的疑问:
初看01背包问题时有个疑问:拿了总比不拿价值要高,这样有什么比较的价值呢?
其实不然,还是回到前面那句话,虽然拿了这件物品,但是代价是空间也减小了,这样面对前面的一些情况时,很有可能想装却装不下了;而没有拿此物品的情况下,空间也没有减少,这意味着剩下的空间还可以装别的东西。
举个例子:
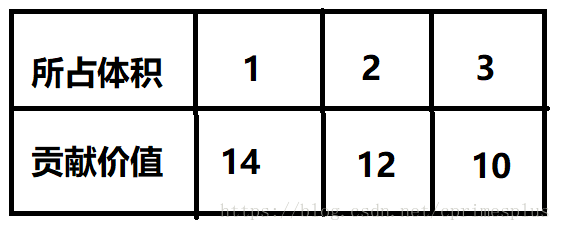
假设背包总容量为4,当前的容量是2。当i=2时,对于第二件物品有拿和不拿两种选择,如果不拿第二件物品,那么可以得到的价值就是14,而后剩余体积变为(2-1=1),dp[1][1]=14,此时14就是极大价值;
如果拿了第二件物品,那么获得的价值就是12,此时体积变为0,dp[1][0]=0,此时的极大价值就是dp[1][0]+12=12;
对比两种极大价值我们不难发现,不拿第二件物品是比拿了第二件物品要好的,因此我们选择不拿。
代码空间上的简化
使用二维数组的目的是,对于第i件物品,他可以通过i-1件物品时的最优解来计算出i件物品的最优解,其实通过一维数组也可以完成这个功能,使用dp[j]来记录剩余空间为j时的最优解。
引用一句话:
由于在01背包问题中,在j - c[i]体积的情况下,里面不能存在c[i]这个物品,也就是说在求状态dp[j]的时候,dp[j -c[i]]还不能被更新过,所以dp[j -c[i]]要放在dp[j]后更新,用递减循环的方式实现这个功能。
反之,如果内层循环顺序进行的话,就代表了在j-c[i]体积的情况下,里面还存有c[i]这个物品,这样对于同一件物品,会计算多次,直到有其他物品加入满足最优解大于一件被计算多次后的值为止。(这样就变成了完全背包问题的求解)
代码部分:
简化前:
for(i=1;i<=N;i++)
{
for(j=space[i];j<=C;j++)
{
dp[i][j]=max(dp[i-1][j],dp[i-1][j-space[i]]+val[i]);
}
}简化后:
for(i=1;i<=N;i++)
{
for(j=C;j>=space[i];j--)
{
dp[j]=max(dp[j],dp[j-space[i]]+val[i]);
}
}完全背包问题
代码(就是将01背包的逆序转化为顺序即可):
for(i=1;i<=N;i++)
{
for(j=space[i];j<=C;j++)
{
dp[j]=max(dp[j],dp[j-space[i]]+val[i]);
}
}