[机器学习] - EM算法与GMM模型

EM算法是一种迭代算法，1977 年由Dempster等人总结提出，用含有隐变量(hidden variable) 的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由两步组成：E步，求期望( expectation)；M步，求极大( maximization)。

方法	适用问题	模型特点	模型类型	学习策略	学习的损失函数	学习算法
EM方法论	概率模型参数估计	含隐变量概率模型	——	极大似然估计，极大后验概率估计	对数似然损失	迭代算法

 

1. EM算法-数学基础

1.1 凸函数

在讲解凸优化问题之前我们先来了解一下凸集和凸函数的概念。
凸集： 在点集拓扑学与欧几里得空间中，凸集是一个点集，其中每两点之间的直线上的点都落在该点集中。如果不明白，请看下图。
　　　　　　　　　　　　　　
凸函数： 一个定义在向量空间的凸子集C(区间)上的实值函数f，如果在其定义域C上的任意两点x，y以及t∈[0,1]有：
　　　　　　　　　　　　　　　　　$f\left(tx+\left(1-t\right)y\right)\le tf\left(x\right)+\left(1-t\right)f\left(y\right)$

则该函数为凸函数！【可以使用拉格朗日中值定理或者是泰勒公式进行证明】。凸函数另一个判别方式是：如果一个凸函数是一个二阶可微函数，则它的二阶导数是非负的。如下图。
　　　　　　　　　　　　　　

注意： 中国大陆数学界某些机构关于函数凹凸性定义和国外的定义是相反的。Convex Function在某些中国大陆的数学书中指凹函数。Concave Function指凸函数。但在中国大陆涉及经济学的很多书中，凹凸性的提法和其他国家的提法是一致的，也就是和数学教材是反的。举个例子，同济大学高等数学教材对函数的凹凸性定义与本条目相反，本条目的凹凸性是指其上方图是凹集或凸集，而同济大学高等数学教材则是指其下方图是凹集或凸集，两者定义正好相反。 另外，也有些教材会把凸定义为上凸，凹定义为下凸。碰到的时候应该以教材中的那些定义为准。

在机器学习领域大多数是采用上文中所描述的凸函数和凹函数的定义。
 
 

1.2 Jensen不等式

定义1： 若f(x)为区间X上的凸函数，则$\forall n\in N,n\ge 1$，若$\forall i\in N,1\le i\le n,x_i\in X,{\lambda }_i\in R$，且${\sum }_{i=1}^n{\lambda }_i=1$, 则：
　　　　　　　　　　　　　　　　　　　　　　$f\left(\sum _{i=1}^n{\lambda }_i{x}_i\right)\le \sum _{i=1}^n{\lambda }_{i}f\left(x_i\right)$
　　　　　　　　　　　　　　　　　
推论1： 若f(x)为区间R上的凸函数，g(x)：R→R为一任意函数，X为一取值范围有限的离散变量，$E[f(g(X))]$与$E[g(X)]$都存在，则：
　　　　　　　　　　　　　　　　　　　　　　$E[f(g(X))]\ge f(E[g(X)])$

 
 

1.3 极大似然估计

       极大似然估计的原理，用一张图片来说明，如下图所示：
　　　　　　　　　　　　　
　　总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

原理： 极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

       由于样本集中的样本都是独立同分布，可以只考虑一类样本集$D$，来估计参数向量$\theta$。记已知的样本集为：
　　　　　　　　　　　　　　　　　　　　　　　　 D = { x 1 , x 2 , . . . . x N } D = \left\{ { {x_1},{x_2},....{x_N}} \right\} D={ x1​,x2​,....xN​}
　　　　　　　　　　　　　　　　　　　　　　
　　似然函数（linkehood function）：联合概率密度函数$p\left(D|\theta \right)$称为相对于 { x 1 , x 2 , . . . . x N } \left\{ { {x_1},{x_2},....{x_N}} \right\} { x1​,x2​,....xN​}的θ的似然函数。
　　　　　　　　　　　　　　　　　$L\left(\theta \right)=p\left(D|\theta \right)=p\left(x_1,x_2,....x_N|\theta \right)=\prod _{i=1}^{N}p\left(x_i|\theta \right)$
　　
　　如果 $\stackrel{\wedge }{\theta }$ 是参数空间中能使似然函数 $l\left(\theta \right)$ 最大的θ值，则 $\stackrel{\wedge }{\theta }$ 应该是“最可能”的参数值，那么就是 $\theta$ 的极大似然估计量。它是样本集的函数，记作：
　　　　　　　　　　　　　　　　　　　　　　$\stackrel{\wedge }{\theta }=d\left(x_1,x_2,....x_N\right)=d\left(D\right)$
　　　　　　　　　　　　　　　　　　　　　
$\stackrel{\wedge }{\theta }\left(x_1,x_2,....x_N\right)$称为极大似然函数的估计值。

 
求解极大似然函数
       ML估计：求使得出现该组样本的概率最大的θ值。
　　　　　　　　　　　　　　　　　　　　$\stackrel{\wedge }{\theta }=\arg \underset{\theta }{\max }l\left(\theta \right)=\arg \underset{\theta }{\max }\prod _{i=1}^{N}p\left(x_i|\theta \right)$
　　　　　　　　　　　　　　　　　　　
　　实际中为了便于分析，定义了对数似然函数：
　　　　　　　　　　　　　　　　　　　　　　　　　　$H\left(\theta \right)=\ln l\left(\theta \right)$
　　　　　　　　　　　　　　$\stackrel{\wedge }{\theta }=\arg \underset{\theta }{\max }H\left(\theta \right)=\arg \underset{\theta }{\max }\ln l\left(\theta \right)=\arg \underset{\theta }{\max }\sum _{i=1}^N\ln p\left(x_i|\theta \right)$
　　　　　　　　　　　　　
(1) 未知参数只有一个（θ为标量）
　　在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：
　　
　　　　　　　　　　　　　　　　　　　　　$\frac{dl\left(\theta \right)}{d\theta }=0$　或　$\frac{dH\left(\theta \right)}{d\theta }=\frac{d\ln l\left(\theta \right)}{d\theta }=0$
　　　　　　　　　　　　　　　　　　　　　
(2) 未知参数有多个（θ为向量）
　　则θ可表示为具有S个分量的未知向量：
　　　　　　　　　　　　　　　　　　　　　　　　　$\theta =[{\theta }_1,{\theta }_2,...,{\theta }_s{]}^T$
　　记梯度算子：
　　　　　　　　　　　　　　　　　　　　　　　${\nabla }_{\theta }=[\frac{\partial }{\partial {\theta }_1},\frac{\partial }{\partial {\theta }_2},...,\frac{\partial }{\partial {\theta }_s}{]}^T$
　　　　　　　　　　　　　　　　　　　　　
　　若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。
　　　　　　　　　　　　　　　　　　${\nabla }_{\theta }H\left(\theta \right)={\nabla }_{\theta }\ln l\left(\theta \right)=\sum _{i=1}^N{\nabla }_{\theta }\ln p\left(x_i|\theta \right)=0$

方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。
 
 

2. EM算法-原理详解

2.1 前言

(1) 　概率模型有时既含有观测变量(observable variable)，又含有隐变量或潜在变量（latent variable），如果仅有观测变量，那么给定数据就能用极大似然估计或贝叶斯估计来估计model参数；但是当模型含有隐变量时，需要一种含有隐变量的概率模型参数估计的极大似然方法估计——EM算法

(2) 　EM算法的标准计算框架由E步（Expectation-step）和M步（Maximization step）交替组成，算法的收敛性可以确保迭代至少逼近局部极大值 。EM算法是MM算法（Minorize-Maximization algorithm）的特例之一，有多个改进版本，包括使用了贝叶斯推断的EM算法、EM梯度算法、广义EM算法等。

(3) 　由于迭代规则容易实现并可以灵活考虑隐变量 ，EM算法被广泛应用于处理数据的缺测值 ，以及很多机器学习（machine learning）算法，包括高斯混合模型（Gaussian Mixture Model, GMM） 和隐马尔可夫模型（Hidden Markov Model, HMM） 的参数估计。
 

2.2 EM算法理论

对于 $m$ 个样本观察数据$x=\left(x^{\left(1\right)},x^{\left(2\right)},....,x^{\left(m\right)}\right)$中，找出样本的模型参数 $\theta$ ，极大化模型分布的对数似然函数如下，
　　　　　　　　　　　　　　　　　　　 　$p\left(X|\theta \right)=\log \prod _{i=1}^{N}p\left(X_i|\theta \right)=\sum _{i=1}^m\log p\left(X_i|\theta \right)$
假设数据中有隐含变量$Z=\left(Z_1,Z_2,....,Z_k\right)$
　　　　　　　　　　　　　　　　　　　　 p ( X ∣ θ ) = ∑ c = 1 k p ( X , Z c ∣ θ ) Z = { Z 1 , . . . . , Z k } p\left( {X|\theta } \right) = \sum\limits_{c = 1}^k {p\left( {X,{Z_c}|\theta } \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Z = \left\{ { {Z_1},....,{Z_k}} \right\} p(X∣θ)=c=1∑k​p(X,Zc​∣θ)Z={ Z1​,....,Zk​}
加入隐含变量公式变为如下，
　　　　　　　　　　　　　　　　　 $\log p\left(X|\theta \right)=\sum _{i=1}^m\log p\left(X_i|\theta \right)=\sum _{i=1}^N\log \left[\sum _{c=1}^{k}p\left(X_i,Z_c|\theta \right)\right]$

上述展开考虑了观测数据的相互独立性。引入与隐变量有关的概率分布 $q(Z)$ ，即隐分布（可认为隐分布是隐变量对观测数据的后验，参见标准算法的E步推导）
　　　　　　　　　　　　　　　$\log p\left(X|\theta \right)=\sum _{i=1}^N\log \left[\sum _{c=1}^{k}p\left(X_i,Z_c|\theta \right)\right]=\sum _{i=1}^N\log \left[\sum _{c=1}^{k}q\left(Z_c\right)\frac{p\left(X_i,Z_c|\theta \right)}{q\left(Z_c\right)}\right]$

由Jensen不等式，log()函数为凹函数，观测数据的对数似然有如下不等关系：
　　　　　　$\log p\left(X|\theta \right)=\sum _{i=1}^N\log \left[\sum _{c=1}^{k}q\left(Z_c\right)\frac{p\left(X_i,Z_c|\theta \right)}{q\left(Z_c\right)}\right]\ge \sum _{i=1}^N\sum _{c=1}^k\left[q\left(Z_c\right)\log \frac{p\left(X_i,Z_c|\theta \right)}{q\left(Z_c\right)}\right]\equiv L\left(\theta ,q\right)$

当 $\theta ,q$ 使不等式右侧取全局极大值时，所得到的$\theta$至少使不等式左侧取局部极大值。因此，将不等式右侧表示为 $L\left(\theta ,q\right)$ 后，$EM$ 算法有如下求解目标：
　　　　　　　　　　　　　　　　　　　　　　　　　　$\stackrel{\wedge }{\theta }=\arg \underset{\theta }{\max }L\left(\theta ,q\right)$
式中的 $L\left(\theta ,q\right)$ 等效于MM算法（Minorize-Maximization algorithm）中的代理函数（surrogate function），是MLE优化问题的下限，EM算法通过最大化代理函数逼近对数似然的极大值。

2.3 EM算法流程

       EM标准算法是一组迭代计算，迭代分为两部分，即E步和M步。其中E步“固定”前一次迭代的${\theta }^{(t)}$ ，构造一个函数 $q_t$ 取目标函数 $\log p\left(X|\theta \right)$ 的下确界；M步 计算 $q_t$ 的最大值${\theta }^{(t+1)}$ ，接下来的E步中，在目标函数的${\theta }^{(t+1)}$处，再构造一个新的下确界函数 $q_{t+1}$，再接下来的M步最大化$q_{t+1}$获取 ${\theta }^{(t+2)}$，直到迭代收敛。
　　　　　　　　　　　　　　
       EM算法在初始化模型参数后开始迭代，迭代中E步和M步交替进行。由于EM算法的收敛性仅能确保局部最优，而不是全局最优。因此通常对EM算法进行随机初始化并多次运行，选择对数似然最大的迭代输出结果。以下给出EM算法E步和M步的推导。

1. E步（Expectation-step, E-step）
   由EM算法的求解目标可知，E步有如下优化问题 ：
   　　　　　　　　　　　　　　
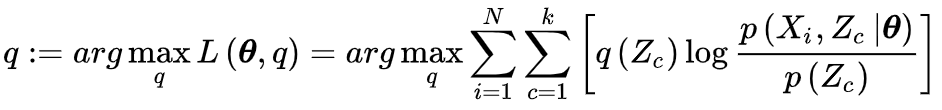
   考虑先前的不等关系，这里首先对 $\log p\left(X|\theta \right)-L\left(\theta ,q\right)$ 进行展 ：
   　　　　　　　　　　　　
   注意到，推导上式时考虑了：$\sum _{c=1}^{k}q\left(Z_c\right)=1$ 由贝叶斯定理（Bayes’ theorem），上式可化为
   　　　　　　　　　　　　　
   式中 KL为Kullback-Leibler散度（Kullback-Leibler divergence, KL）或相对熵（relative entropy），$F\left(\theta ,q\right)$ 表示吉布斯自由能（Gibbs free energy）。
   　　　　　　　　　　　　　　　　
   即由Jensen不等式得到的代理函数等价于隐分布的自由能。求解 $L\left(\theta ,q\right)$ 的极大值等价于求解隐分布自由能的极大值，即隐分布对隐变量后验 $p\left(Z|X,\theta \right)$ 的KL散度的极小值。由 KL 散度的性质可知，其极小值在两个概率分布相等时取得，因此当$q(Z)=p\left(Z|X,\theta \right)$ 时， $L\left(\theta ,q\right)$ 取极大值，对EM算法的第 $t$ 次迭代，E步有如下计算：
   　　　　　　　　　　　　　　　　

      2. M步（Maximization step, M-step）
在E步的基础上，M步求解模型参数使 $L\left(\theta ,q\right)$ 取极大值。该极值问题的必要条件是$\frac{\partial L\left(\theta ,q\right)}{\partial \theta }=0$：
　　　　　　　　　　　　　　　　
式中 ${\mathrm{E}}_q$ 表示联合似然 $p\left(X,Z|\theta \right)$ 对隐分布 $q(Z)$ 的数学期望。在 $\log p\left(X,Z|\theta \right)$ 为凸函数时（例如隐变量和观测服从指数族分布），上述推导也是充分的 。由此得到M步的计算：
　　　　　　　　　　　　　　　　　　　　

2.4 总结

如果我们从算法思想的角度来思考EM算法，我们可以发现我们的算法里已知的是观察数据，未知的是隐含数据和模型参数，在E步，我们所做的事情是固定模型参数的值，优化隐含数据的分布，而在M步，我们所做的事情是固定隐含数据分布，优化模型参数的值。

本节介绍的EM算法是通用的EM算法框架，其实EM算法有很多实现方式，其中比较流行的一种实现方式是高斯混合模型（Gaussian Mixed Model）。
 
 

3. EM算法高斯混合模型GMM

3.1 GMM介绍

GMM(Gaussian mixture model) 混合高斯模型在机器学习、计算机视觉等领域有着广泛的应用。其典型的应用有概率密度估计、背景建模、聚类等。

高斯混合模型（Gaussian Mixed Model）指的是多个高斯分布函数的线性组合，理论上GMM可以拟合出任意类型的分布，通常用于解决同一集合下的数据包含多个不同的分布的情况。
　　　　　　　　　　　　　　　

3.2 GMM原理解析

根据我们上一节写的 EM算法-原理详解 ，我们已经学习了EM算法的一般形式：
　　　　　　　　　　　　　　　　　　　　 p ( X ∣ θ ) = ∑ c = 1 k p ( X , Z c ∣ θ ) Z = { Z 1 , . . . . , Z k } p\left( {X|\theta } \right) = \sum\limits_{c = 1}^k {p\left( {X,{Z_c}|\theta } \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Z = \left\{ { {Z_1},....,{Z_k}} \right\} p(X∣θ)=c=1∑k​p(X,Zc​∣θ)Z={ Z1​,....,Zk​}
　　　　　　　　　　　　　　　　　　　　$L\left(\theta ,q\right)=\sum _{i=1}^N\sum _{c=1}^k\left[q\left(Z_c\right)\log \frac{p\left(X_i,Z_c|\theta \right)}{q\left(Z_c\right)}\right]$
　　　　　　　　　　　　　　　　　　　　　　　　　$\sum _{c=1}^{k}q\left(Z_c\right)=1$
　　　　　　　　　　　　　　　　　　　　　　　　　
由GMM的一般定义可知，其似然和参数有如下表示 ：
　　　　　　　　　　　　　　　　　　　
根据学习数据的维度，式中：

1. $N\left(\mu ,{\sigma }^2\right)$ 表示均值为 $\mu$ ，方差/协方差为 ${\sigma }^2$ 的正态分布/联合正态分布。
2. $\pi$ 为正态分布的混合比例。
3. $k$ 为参与混合的分布总数。

定义与观测数据有关的隐变量：$Z\to X$ ，令隐分布 $q(Z)$ 表示GMM聚类的软指定（soft assignment），即每个数据来源于第 c ∈ { 1 , . . . . , k } c \in \left\{ {1,....,k} \right\} c∈{ 1,....,k} 个分布的概率，则隐变量有离散取值 Z = { Z 1 , . . . . , Z k } Z = \left\{ { {Z_1},....,{Z_k}} \right\} Z={ Z1​,....,Zk​} 。

将上述内容带入EM算法的计算框架后，E步有如下展开：
　　　　　　　　　　　　　　　
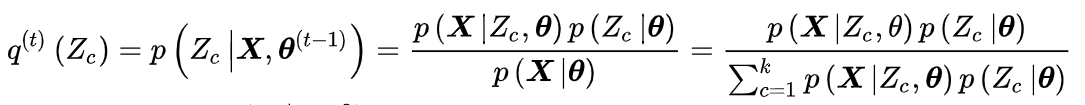
GMM中有：
　　　　　　　　　　　　　　　　　　　　
因此，E步的计算步骤为：
　　　　　　　　　　　　　　　　　　
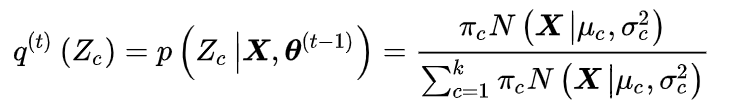
M步的计算步骤为： 通过E步输出的隐变量后验计算模型参数，在GMM中，M步计算框架的优化问题有如下表示：
　　　　　　　　　　　　　　　
不失一般性，带入单变量正态分布的解析形式后对模型参数求偏导数可得M步的计算步骤 ：
　　　　　　　　　　　　　　　

3.3 GMM算法流程

输入：观测数据 $y_1,y_2,y_3,...,y_N$
输出：GMM的参数

1. 初始化参数
2. E步：根据当前模型，计算分模型 $k$ 对 观察数据$y_j$ 的相应度:
   　　　　　　　　　　　　　　　　　
3. M步：计算新一轮迭代的模型参数：
   　　　　　　　　　　　　　　　　　　　　　
   　　　　　　　　　　　　　　　　　　　　
   　　　　　　　　　　　　　　　　　　　　
4. 重复第（2）步和第（3）步，直到收敛
    
    

4. EM算法-高斯混合模型GMM详细代码实现

4.1 GMM算法实现

我的实现逻辑基本按照GMM算法流程中的方式实现。
输入：观测数据 $x_1,x_2,x_3,...,x_N$

（1）输入数据进行归一化处理

#数据预处理
def scale_data(self):
    for d in range(self.D):
        max_ = self.X[:, d].max()
        min_ = self.X[:, d].min()
        self.X[:, d] = (self.X[:, d] - min_) / (max_ - min_)
    self.xj_mean = np.mean(self.X, axis=0)
    self.xj_s = np.sqrt(np.var(self.X, axis=0))

（2）输出：GMM的参数

1. 初始化参数

#初始化参数
def init_params(self):
    self.mu = np.random.rand(self.K, self.D)
    self.cov = np.array([np.eye(self.D)] * self.K) * 0.1
    self.alpha = np.array([1.0 / self.K] * self.K)

2. E步：根据当前模型，计算模型 $k$ 对 $y_i$ 的影响
   　　　　　　　　　　　　　　　　　

#e步，估计gamma
def e_step(self, data):
    gamma_log_prob = np.mat(np.zeros((self.N, self.K)))
    for k in range(self.K):
        gamma_log_prob[:, k] = log_weight_prob(data, self.alpha[k], self.mu[k], self.cov[k])
    log_prob_norm = logsumexp(gamma_log_prob, axis=1)
    log_gamma = gamma_log_prob - log_prob_norm[:, np.newaxis]
    return log_prob_norm, np.exp(log_gamma)

3. M步：计算$\stackrel{\wedge }{{\mu }_k}$，$\stackrel{\wedge }{{\sigma }_k}$，$\stackrel{\wedge }{{\alpha }_k}$。
   　　　　　　　　　　　　　　　　　　　　
   　　　　　　　　　　　　　　　　　　　　
   　　　　　　　　　　　　　　　　　　　　

#m步，最大化loglikelihood
def m_step(self):
    newmu = np.zeros([self.K, self.D])
    newcov = []
    newalpha = np.zeros(self.K)
    for k in range(self.K):
        Nk = np.sum(self.gamma[:, k])
        newmu[k, :] = np.dot(self.gamma[:, k].T, self.X) / Nk
        cov_k = self.compute_cov(k, Nk)
        newcov.append(cov_k)
        newalpha[k] = Nk / self.N
    newcov = np.array(newcov)
    return newmu, newcov, newalpha

4. 重复2，3两步直到收敛
   最后加上loglikelihood的计算方法。
   基本的计算方法按照公式定义。
   　　　　　　　　　　　　　　　$\log p\left(X|\theta \right)=\sum _{i=1}^N\log \left[\sum _{c=1}^{k}p\left(X_i,Z_c|\theta \right)\right]=\sum _{i=1}^N\log \left[\sum _{c=1}^{k}q\left(Z_c\right)\frac{p\left(X_i,Z_c|\theta \right)}{q\left(Z_c\right)}\right]$
   　　　　　　　　　　　　　　　　　　　　　　　　　$\sum _{c=1}^{k}q\left(Z_c\right)=1$

def loglikelihood(self):
    P = np.zeros([self.N, self.K])
    for k in range(self.K):
        P[:,k] = prob(self.X, self.mu[k], self.cov[k])

    return np.sum(np.log(P.dot(self.alpha)))

 
 
补充：
可以参考百度百科，使用EM算法求解GMM的编程实现：

# 导入模块
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal

# 构建测试数据
N = 200; pi1 = np.array([0.6, 0.3, 0.1])
mu1 = np.array([[0,4], [-2,0], [3,-3]])
sigma1 = np.array([[[3,0],[0,0.5]], [[1,0],[0,2]], [[.5,0],[0,.5]]])
gen = [np.random.multivariate_normal(mu, sigma, int(pi*N)) for mu, sigma, pi in zip(mu1, sigma1, pi1)]
X = np.concatenate(gen)

# 初始化: mu, sigma, pi = 均值, 协方差矩阵, 混合系数
theta = {
    
    }; param = {
    
    }
theta['pi'] = [1/3, 1/3, 1/3]            # 均匀初始化
theta['mu'] = np.random.random((3, 2))   # 随机初始化
theta['sigma'] = np.array([np.eye(2)]*3) # 初始化为单位正定矩阵
param['k'] = len(pi1); param['N'] = X.shape[0]; param['dim'] = X.shape[1]

# 定义函数
def GMM_component(X, theta, c):
    '''
    由联合正态分布计算GMM的单个成员
    '''
    return theta['pi'][c]*multivariate_normal(theta['mu'][c], theta['sigma'][c, ...]).pdf(X)
 
def E_step(theta, param):
    '''
    E步：更新隐变量概率分布q(Z)。
    '''
    q = np.zeros((param['k'], param['N']))
    for i in range(param['k']):
        q[i, :] = GMM_component(X, theta, i)
    q /= q.sum(axis=0)
    return q
 
def M_step(X, q, theta, param):
    '''
    M步：使用q(Z)更新GMM参数。
    '''
    pi_temp = q.sum(axis=1); pi_temp /= param['N'] # 计算pi
    mu_temp = q.dot(X); mu_temp /= q.sum(axis=1)[:, None] # 计算mu
    sigma_temp = np.zeros((param['k'], param['dim'], param['dim']))
    for i in range(param['k']):
        ys = X - mu_temp[i, :]
        sigma_temp[i] = np.sum(q[i, :, None, None]*np.matmul(ys[..., None], ys[:, None, :]), axis=0)
    sigma_temp /= np.sum(q, axis=1)[:, None, None] # 计算sigma
    theta['pi'] = pi_temp; theta['mu'] = mu_temp; theta['sigma'] = sigma_temp
    return theta
 
def likelihood(X, theta):
    '''
    计算GMM的对数似然。
    '''
    ll = 0
    for i in range(param['k']):
        ll += GMM_component(X, theta, i)
    ll = np.log(ll).sum()
    return ll
 
def EM_GMM(X, theta, param, eps=1e-5, max_iter=1000):
    '''
    高斯混合模型的EM算法求解
        theta: GMM模型参数; param: 其它系数; eps: 计算精度; max_iter: 最大迭代次数
        返回对数似然和参数theta，theta是包含pi、mu、sigma的Python字典
    '''
    for i in range(max_iter):
        ll_old = 0
        # E-step
        q = E_step(theta, param)
        # M-step
        theta = M_step(X, q, theta, param)
        ll_new = likelihood(X, theta)
        if np.abs(ll_new - ll_old) < eps:
            break;
        else:
            ll_old = ll_new
    return ll_new, theta
    
# EM算法求解GMM，最大迭代次数为1e5
ll, theta2 = EM_GMM(X, theta, param, max_iter=10000)

# 由theta计算联合正态分布的概率密度
L = 100; Xlim = [-6, 6]; Ylim = [-6, 6]
XGrid, YGrid = np.meshgrid(np.linspace(Xlim[0], Xlim[1], L), np.linspace(Ylim[0], Ylim[1], L))
Xout = np.vstack([XGrid.ravel(), YGrid.ravel()]).T
MVN = np.zeros(L*L)
for i in range(param['k']):
    MVN += GMM_component(Xout, theta, i)
MVN = MVN.reshape((L, L))

# 绘制结果
plt.plot(X[:, 0], X[:, 1], 'x', c='gray', zorder=1)
plt.contour(XGrid, YGrid, MVN, 5, colors=('k',), linewidths=(2,))
plt.show()

5 总结