问题
设想一个在一维空间的物块,在其上施加一个力f,物块会运动:
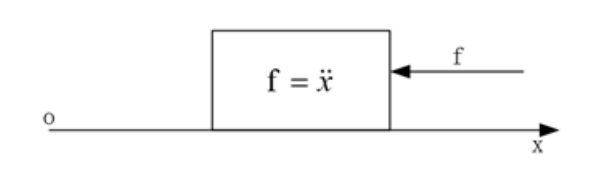
显然这是一个二阶系统,选取状态变量 x 1 x_1 x1为位移, x 2 x_2 x2为速度,则有:
x 1 ˙ = x 2 x 2 ˙ = f / m = u \dot{x_1}=x_2\\\dot{x_2}=f/m=u x1˙=x2x2˙=f/m=u
其中 u u u定义为输入, m m m为物块的质量。又已知:
x 1 ( 0 ) = 1 x 2 ( 0 ) = 0 x_1(0) = 1\\x_2(0)=0 x1(0)=1x2(0)=0
设计一个滑模控制器将其控制到原点。
设计滑模面和控制率
滑模面其实就是一个将状态变量融合后的量,是一个n维空间的面,因此也称为滑模面,这里因为只有两个状态变量,就设计成如下形式:
s = c x 1 + x 2 s=cx_1+x_2 s=cx1+x2
两端对时间求导:
s ˙ = c x 1 ˙ + x 2 ˙ = c x 2 + u \dot{s}=c\dot{x_1}+\dot{x_2}=cx_2+u s˙=cx1˙+x2˙=cx2+u
移项有控制量的表达式:
u = s ˙ − c x 2 u=\dot{s}-cx_2 u=s˙−cx2
而 s ˙ \dot{s} s˙可以设计成 − ε s g n ( s ) , ε > 0 -\varepsilon sgn(s),\varepsilon>0 −εsgn(s),ε>0。因此:
u = − ε s g n ( s ) − c x 2 u=-\varepsilon sgn(s)-cx_2 u=−εsgn(s)−cx2
其中:
s g n ( x ) = { 1 , x > 0 0 , x = 0 − 1 , x < 0 sgn(x)=\left\{\begin{array}{c}1,x>0\\0,x=0\\-1,x<0\end{array}\right. sgn(x)=⎩⎨⎧1,x>00,x=0−1,x<0
MATLAB验证
分别验证了在f无干扰和有干扰情况下物块的控制效果:
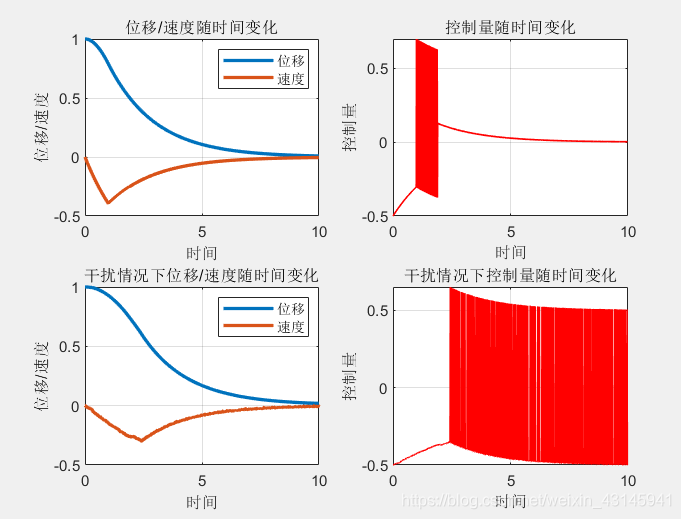
从图中可以看到,物块最终稳定在位移为0的地方,速度也趋于0,控制目的达到,至于效果,与 ε , c \varepsilon,c ε,c有关。
代码:
%滑模控制一维方块控制demo1(不考虑干扰)
%初始化
deltaT = 0.01;
x1 = [];%位移
x2 = [];%速度
u = [];%控制量
x1(1) = 1; x2(1) = 0;
c = 0.5; e = 0.5;
%循环
iter = 1000;
for i = 1:iter - 1
s = 0.5*x1(i) + x2(i);
if(s>0)
ui = -e - c*x2(i);
u = [u,ui];
end
if(s<0)
ui = e - c*x2(i);
u = [u,ui];
end
if(s==0)
ui = -c*x2(i);
u = [u,ui];
end
x2(i+1) = x2(i) + ui*deltaT;
x1(i+1) = x1(i) + x2(i)*deltaT;
end
subplot(2,2,1)
plot(0:deltaT:(iter-1)*deltaT,x1,"LineWidth",2)
xlabel("时间"),ylabel("位移/速度"),title("位移/速度随时间变化")
hold on; grid on;
plot(0:deltaT:(iter-1)*deltaT,x2,"LineWidth",2)
legend("位移","速度")
subplot(2,2,2)
plot(0:deltaT:(iter-2)*deltaT,u,"LineWidth",1,'Color','r')
xlabel("时间"),ylabel("控制量"),title("控制量随时间变化");grid on;
%demo2(考虑干扰)
x1 = [];%位移
x2 = [];%速度
u = [];%控制量
x1(1) = 1; x2(1) = 0;
for i = 1:iter - 1
s = 0.5*x1(i) + x2(i);
if(s>0)
ui = -e - c*x2(i);
u = [u,ui];
end
if(s<0)
ui = e - c*x2(i);
u = [u,ui];
end
if(s==0)
ui = -c*x2(i);
u = [u,ui];
end
x2(i+1) = x2(i) + (ui+rand*0.6)*deltaT;
x1(i+1) = x1(i) + x2(i)*deltaT;
end
subplot(2,2,3)
plot(0:deltaT:(iter-1)*deltaT,x1,"LineWidth",2)
xlabel("时间"),ylabel("位移/速度"),title("干扰情况下位移/速度随时间变化")
hold on; grid on;
plot(0:deltaT:(iter-1)*deltaT,x2,"LineWidth",2)
legend("位移","速度")
subplot(2,2,4)
plot(0:deltaT:(iter-2)*deltaT,u,"LineWidth",1,'Color','r')
xlabel("时间"),ylabel("控制量"),title("干扰情况下控制量随时间变化");grid on;
对 ε , c \varepsilon,c ε,c的分析
原始的 ε = 0.5 , c = 0.5 \varepsilon =0.5,c=0.5 ε=0.5,c=0.5,现改为 ε = 0.5 , c = 2.5 \varepsilon =0.5,c=2.5 ε=0.5,c=2.5:
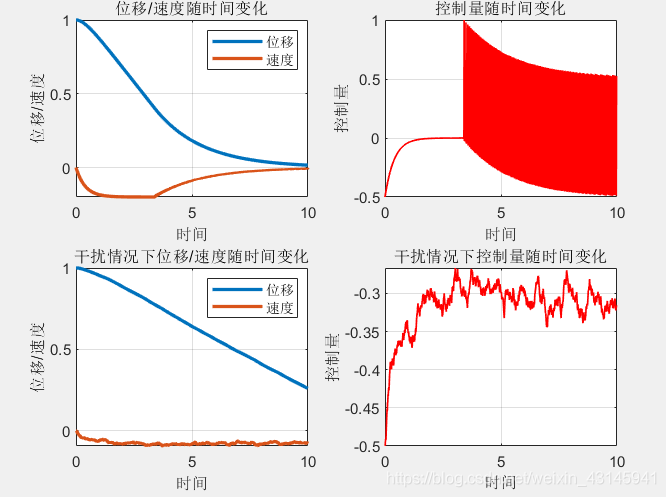
看起来系统的抗干扰性减弱了,具体理论分析有待解决。
ε = 2.5 , c = 0.5 \varepsilon =2.5,c=0.5 ε=2.5,c=0.5:

控制器大幅度振荡,类似振铃现象。
ε = 0.2 , c = 0.5 \varepsilon =0.2,c=0.5 ε=0.2,c=0.5:
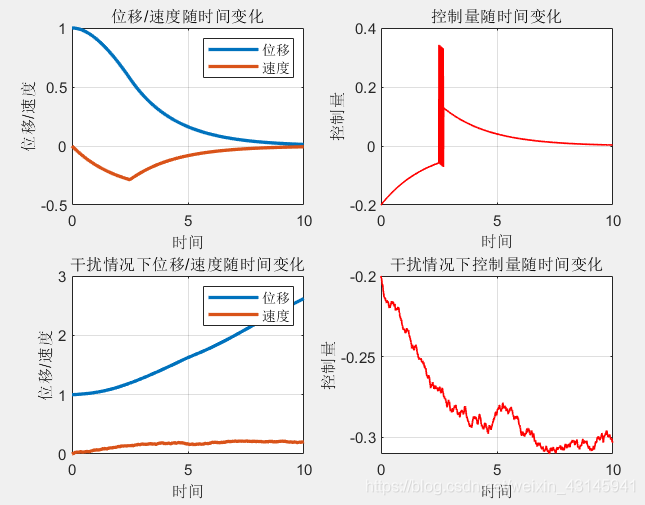
有干扰的系统不稳定了,这个可通过如下方式间接证明:
x 1 ˙ = x 2 x 2 ˙ = u + d \dot{x_1}=x_2\\\dot{x_2}=u+d x1˙=x2x2˙=u+d
其中 d d d为干扰。
构造Lyapunov函数:
V = 0.5 s 2 V=0.5s^2 V=0.5s2
显然Lyapunov第一条件满足,验证第二条件:
V ˙ = s s ˙ = s ( − ε s g n ( s ) + d ) = − ε ∣ s ∣ + s d ≤ − ε ∣ s ∣ + ∣ s ∣ L = − ∣ s ∣ ( ε − L ) L = m a x { ∣ d ∣ } \dot{V}=s\dot{s}=s(-\varepsilon sgn(s)+d)=-\varepsilon |s|+sd\leq -\varepsilon|s|+|s|L=-|s|(\varepsilon - L)\\ L=max\{|d|\} V˙=ss˙=s(−εsgn(s)+d)=−ε∣s∣+sd≤−ε∣s∣+∣s∣L=−∣s∣(ε−L)L=max{
∣d∣}
若满足负定则:
− ∣ s ∣ ( ε − L ) ≤ 0 → ε ≥ L -|s|(\varepsilon - L)\leq0\rightarrow \varepsilon\geq L −∣s∣(ε−L)≤0→ε≥L
也就是说 ε \varepsilon ε不能太小了,否则s不能趋于0,而滑模控制s必须趋于0状态才能收敛到原点。
V ˙ ≤ − α V \dot{V}\leq-\alpha\sqrt{V} V˙≤−αV
改进Lyapunov第二条件为标题所述可以加快调节时间,上式对时间积分:
∫ 0 t V ˙ V d t ≤ − α t \int^t_0\frac{\dot{V}}{\sqrt{V}}dt\leq-\alpha t ∫0tVV˙dt≤−αt
得到:
V ( t ) ≤ − 0.5 α t + V ( 0 ) \sqrt{V(t)}\leq-0.5\alpha t+\sqrt{V(0)} V(t)≤−0.5αt+V(0)
令:
− 0.5 α t r + V ( 0 ) = 0 -0.5\alpha t_r+\sqrt{V(0)}=0 −0.5αtr+V(0)=0
则:
t r = 2 V ( 0 ) α t_r=\frac{2\sqrt{V(0)}}{\alpha} tr=α2V(0)
同样利用Lyapunov方法第二条件计算 ε \varepsilon ε的取值范围得:
ε ≥ α 2 \varepsilon \ge \frac{\alpha}{\sqrt2} ε≥2α
t r t_r tr越小, α \alpha α越大,需要的 ε \varepsilon ε越大才能保证Lyapunov函数负定。
Simulink仿真一个二阶系统的SMC控制
被控对象具有以下数学描述(model中使用s-Func搭建):
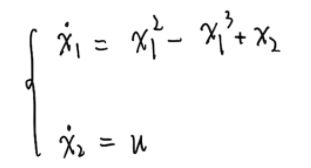
控制率求解:
s = c ( x 1 − x d ) s ˙ = c x 1 ˙ + x 2 ˙ = c ( x 1 2 − x 1 3 + x 2 ) + u = k s g n ( s ) u = − c ( x 1 2 − x 1 3 + x 2 ) − k s g n ( s ) s=c(x_1-x_d)\\ \dot{s}=c\dot{x_1}+\dot{x_2}=c(x_1^2-x_1^3+x_2)+u=ksgn(s)\\ u=-c(x_1^2-x_1^3+x_2)-ksgn(s) s=c(x1−xd)s˙=cx1˙+x2˙=c(x12−x13+x2)+u=ksgn(s)u=−c(x12−x13+x2)−ksgn(s)
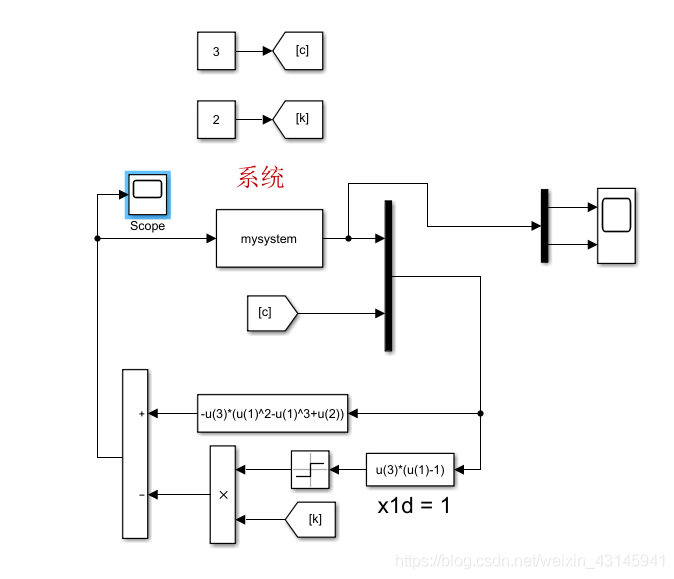
结果:
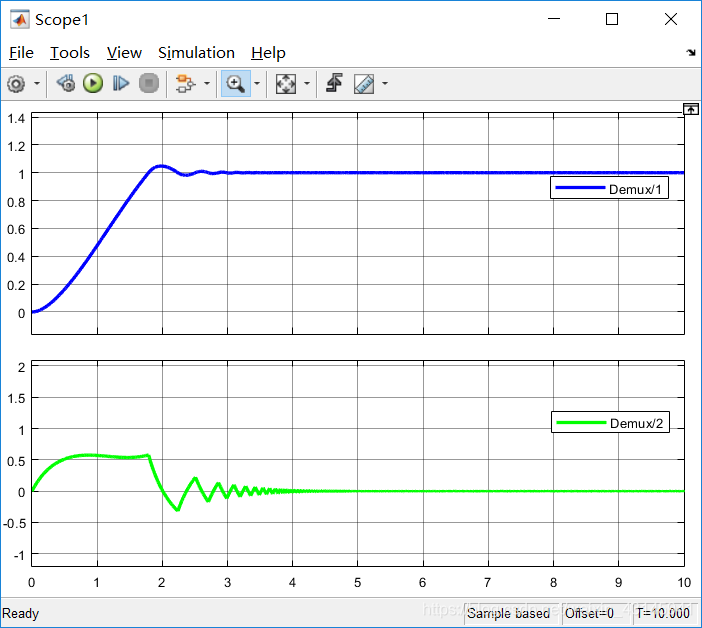
蓝色曲线为 x 1 x_1 x1,绿色曲线为 x 2 x_2 x2。
滑模控制的优点和不足
优点是设计简单,为非线性控制提供了一种general的方法(相比于backstepping等),不足的话比如这个例子中控制量会存在剧烈震荡现象。