Gauss消元的部分主元法和完全主元法(补充)

本文主要是对下文的补充，而补充的主要内容就是如何直接求出(手动)部分主元法的P矩阵和L矩阵：

线性代数 --- Gauss消元的部分主元法和完全主元法_松下J27的博客-CSDN博客_高斯消元的主元是什么Gauss消元的部分主元法和完全主元法https://blog.csdn.net/daduzimama/article/details/124797212

在我之前写的文章中，我留下了一个问题。那就是，在高斯消元的过程中，如果使用了行交换（或者列交换），怎么才能像不选主元法那样直接写出标准的下三角L矩阵呢？以及如何直接写出P矩阵，使得：PA=LU呢？后面，分别有两个热心的网友留言，并进行了答复。其中有一个网友的留言，我已经做了验证，并把他所说的算法补充到了原文中。后来，又有一位网友留言，同时推荐了一本书（如下图）：

这里面详细介绍了直接写出标准下三角矩阵L和置换矩阵P的办法。且，这本书里的方法和我前文中的方法不完全一样（可以说更好)，但也有相似之处，现在我就把数中的方法写出来。由于那本书中对矩阵的命名和我前文的命名有很大的不同，这里我依然沿用原书中的命名。

Part I: Lloyd书中不选主元法的表示方式

1，首先，为了便于比较，我们依然沿用原来的例子：

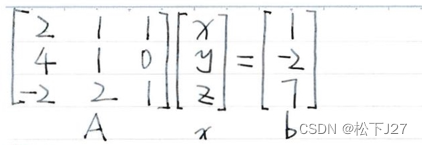
就不选主元法而言，这本书没有使用基本消元矩阵E来记录高斯消元的过程。而是把主元下面所有元素的消元过程都放在一个矩阵中(或者说是用一个矩阵来记录一整列的消元过程)，书中用带有下标的 $\large L_{n}$ 矩阵表示。

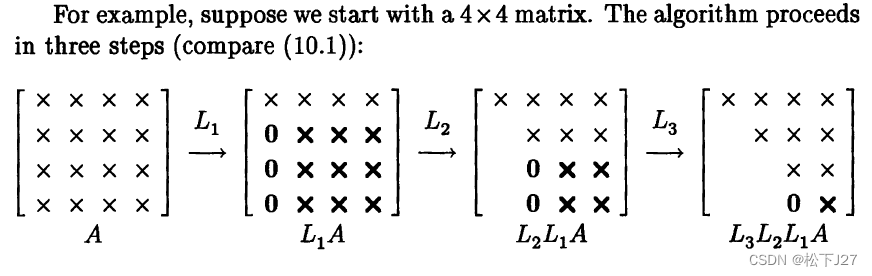
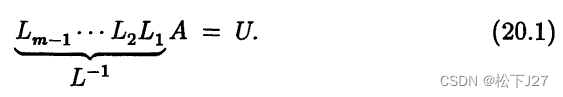
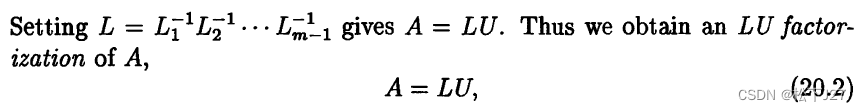
为了便于比较，我这里也把用消元矩阵 $E_{xy}$ 来表示的做法用书中的方式画下来了:

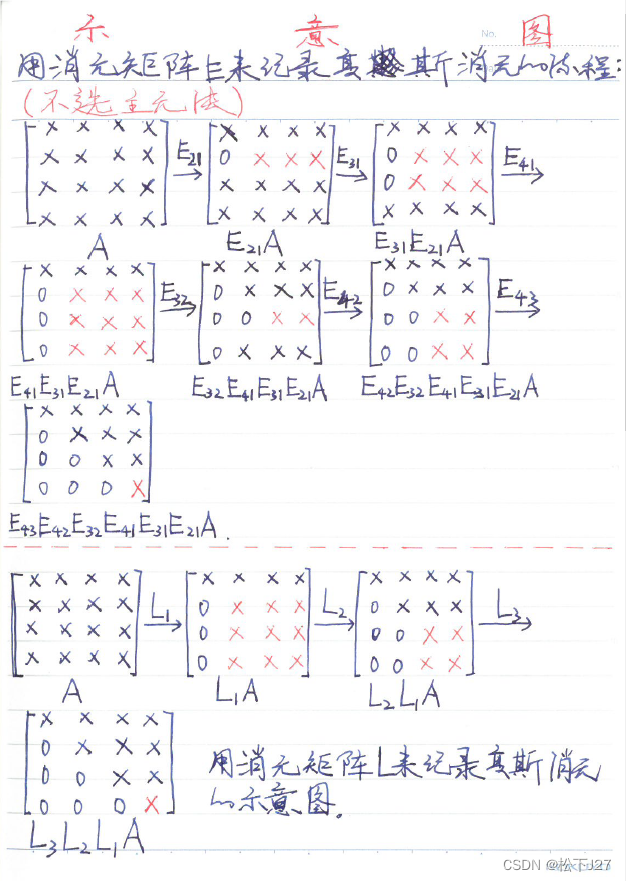
前者是用 $E_{nn-1}...E_{n2}...E_{42}E_{32}E_{n1}...E_{31}E_{21}A$ 来表示（或记录）消元的过程，而后者是用 $L_{n-1}...L_{2}L_{1}A$ 来表示消元的过程。而且，从上面的列子，我们可以看出对于4x4的矩阵而言：

$\large E_{41}E_{31}E_{21}=L_{1}$

$\large E_{42}E_{32}=L_{2}$

$\large E_{43}=L_{3}$

2，此外，书中的L矩阵同样用到了基本消元矩阵的两个性质：

2.1，若要计算基本消元矩阵 $E_{xy}$ 的逆，只需改变矩阵 $E_{xy}$ 中第x行，第y列元素的符号即可。

例如（这不是本文起始处Ax=b所对应的消元矩阵）：

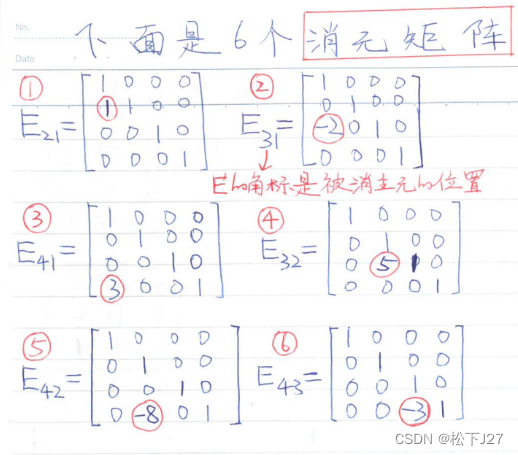
6个消元矩阵的逆（只需改变对应元素的符号即可）

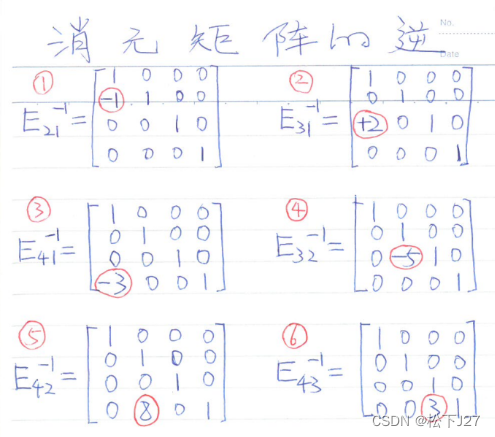
2.2，要求多个的消元矩阵(例子中为消元矩阵的逆)的乘积，只需在单位矩阵I中，逐一填入 $E_{xy}$ 对应位置的值即可。

例如：

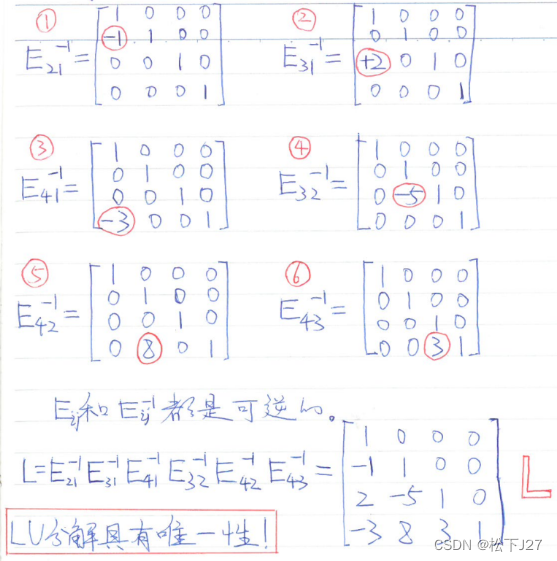
只不过，在这个作者的书中，他是以整列为单位操作的（即，以 $\large L_{n}$ 矩阵为单位处理的)，如下：

并且，他在书中把上文中提到的消元矩阵 $E_{xy}$ 的两个特性称为两个LUCK“ two stroke of luck”。

Luck 1(20.4)：等同于消元矩阵E的第一条属性，即，逆矩阵只需改变对应元素的符号即可:

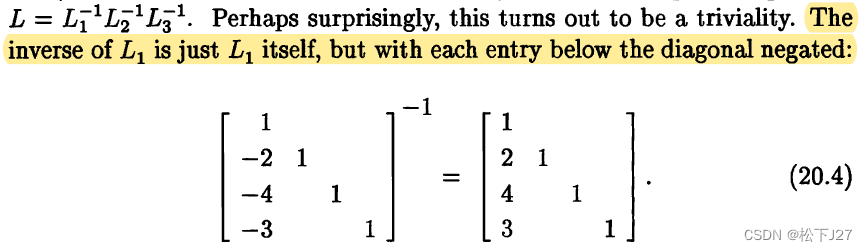
Luck 2(20.5)：等同于消元矩阵E的第二个属性，即，要求多个E的乘积，只需把E中的元素逐一填入单位矩阵I中对应的位置即可。

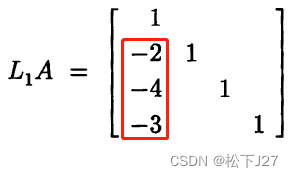
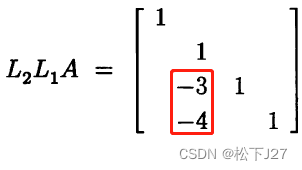
把L1，L2和L3中用红色方框框出来的元素（改变符号后，因为下图中为L的逆)，逐一放在单位矩阵I中对应的位置，即可生成L矩阵。

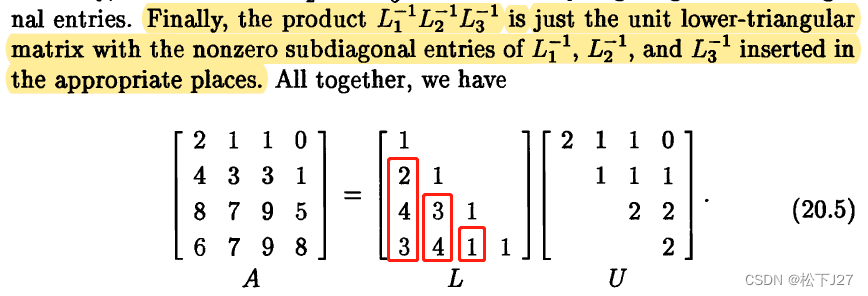
按照这位作者Lloyd N. Trefethen的做法，我也把用多个消元矩阵 $E_{xy}$ 相乘的表示方式和用文中多个 $\large L_{n}$ 矩阵相乘的表示方式做了一个类比：

相当于是Lloyd所使用的每一个 $\large L_{n}$ 都恰好是第n列所对应的全部E矩阵相乘的结果。

Part II: Lloyd书中部分主元法的表示方式

不选主元法，并不是本文的重点。下面我们看看在他的书中，如果遇到了行交换的问题，他是怎么直接写出L矩阵的。

1，首先，他在这里也是用P表示置换矩阵。

2，和用消元矩阵E+置换矩阵P的表示方式一样，他也是按照从A到U的消元过程，按照消元的顺序，把整个消元过程用若干个置换矩阵P和消元矩阵L的乘积表示。（唯一不同的就是在我的方法中用的是E矩阵，而在他的方法中用的是L矩阵）

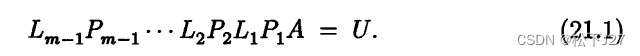
我们先看看书中的一个例子，以便更好的理解他的做法，尤其要注意他的L'矩阵：

（下图中的L1应为L2）

最终，按照从A到U的消元顺序得到：

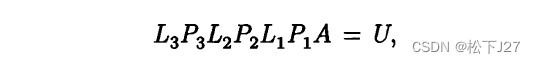
注意：这里L3P3L2P2L1P1逐一相乘后的结果和前面不选主元法的例子中得到的L3L2L1可不一样，由于置换矩阵P的存在，他得到的不是一个标准的下三角矩阵，但后者（L3L2L1）是，且后者的逆也是。

不选主元法中L3L2L1的结果：

L3L2L1和他的逆都是下三角矩阵，且他的逆可以直接根据L1,L2和L3写出来

而L3P3L2P2L1P1的结果这样的：

注意，因为P矩阵的引入，L3P3L2P2L1P1的乘积不是下三角矩阵

更重要的是，在有P矩阵的情况下，你无法按照原来的方法直接写出标准的下三角矩阵L。

但，这本书的作者提到了一个可以直接写出标准下三角矩阵L的办法，并称之为第三个luck：

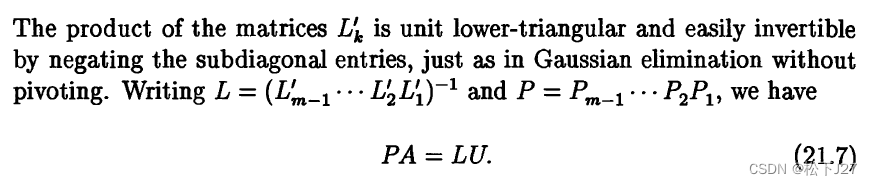
用他的话说就是，我们最终想得到的PA=LU中的P和L，他们分别由：

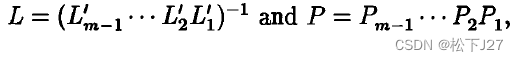
和

给出。

举个例子吧，如果是用部分主元法对一个4x4的矩阵消元，则我们所需要的L1',L2'和L3'分别是：

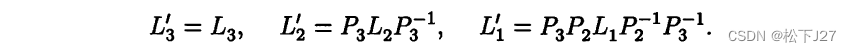
而最终的L等于：

$\large L=(L_{3}^{'}L_{2}^{'}L_{1}^{'})^{-1}={L_{1}^{'}}^{-1}{L_{2}^{'}}^{-1}{L_{3}^{'}}^{-1}$

分别代入上面的L1',L2'和L3'得到：

$\large L=(P^{3}P^{2}L^{1}{P^{2}}^{-1}{P^{3}}^{-1})^{-1}(P^{3}L^{2}{P^{3}}^{-1})^{-1}(L^{3})^{-1}$

我们按照书中的说法做一遍，看看最终的结果：

最后，我用他的这个方法来计算本文最开始的那个例子，有兴趣的读者可以和我原文中用消元矩阵E+置换矩阵P的算法算法做个对比：（尤其是要注意PnLn左乘和LnPn右乘的区别，以及右乘对最终L矩阵的影响，我想这就是作者所说的第三个Luck吧）

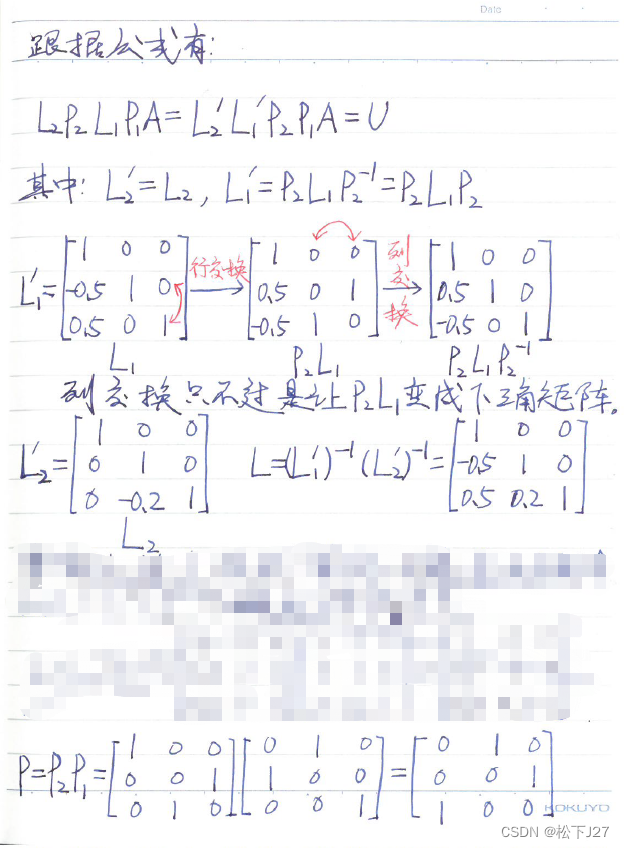
这里我们要注意两点：

1，在计算Ln'矩阵时要注意：Ln'等于若干个置换矩阵P左乘Ln和若干置换矩阵P的逆右乘Ln。

当我们自己手算时(也许包括编程时)，如果注意到Ln后面所乘的一系列的置换矩阵P的逆，都只是为了把前面PPPP...PLn的结果变成下三角矩阵而已的话。

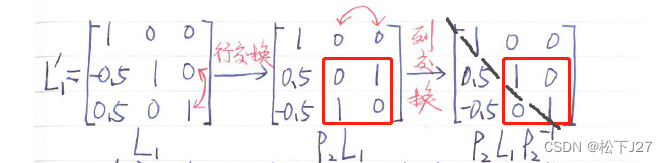
且，我们在写L矩阵时也只是用到了Ln'中的第n列主元下面的值(要改变符号)，完全不需要考虑他究竟是不是标准的下三角矩阵，也就是说大可不需要Ln后面的一系列的列交换操作，依然也能写出L矩阵。

这样一来我们在计算Ln'时，可以选择一种取巧的办法，不去管Ln后面的P，只需把PPPP...PLn乘起来即可。

2，私以为，他的这种表示方法，有一个地方可以改进，那就是把P1，P2。。。的命名方式改成P14(交换14行),P23(交换23行)可能会更好，这样更直观一些。但，似乎又不利于计算Ln时的排序。。。

（全文完）

作者 --- 松下J27

古诗词赏析：

《破阵子·为陈同甫赋壮词以寄》

---辛弃疾

醉里挑灯看剑，梦回吹角连营。八百里分麾下炙，五十弦翻塞外声，沙场秋点兵。
马作的卢飞快，弓如霹雳弦惊。了却君王天下事，赢得生前身后名。可怜白发生！

参考文献（鸣谢）：

《Numerical Linear Algebra》---Lloyd N. Trefethen, David Bau

（配图与本文无关）

线性代数 --- Gauss消元的部分主元法和完全主元法(补充)

Gauss消元的部分主元法和完全主元法(补充)

Part I: Lloyd书中不选主元法的表示方式

Part II: Lloyd书中部分主元法的表示方式

猜你喜欢