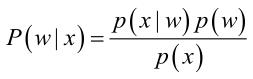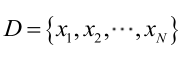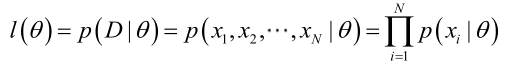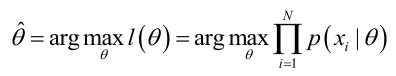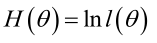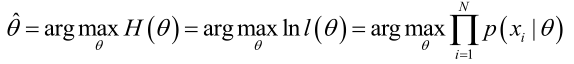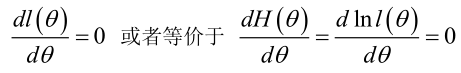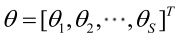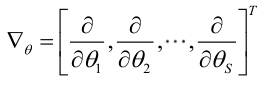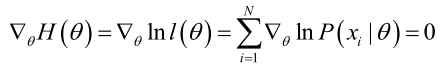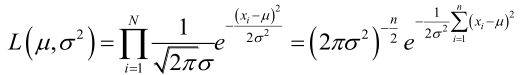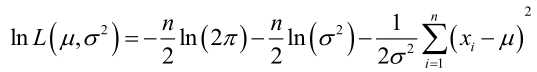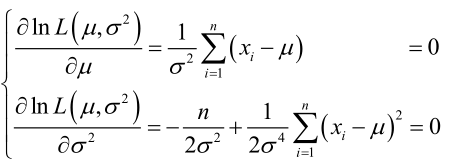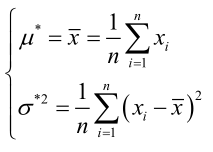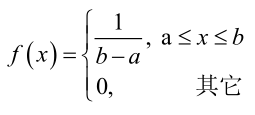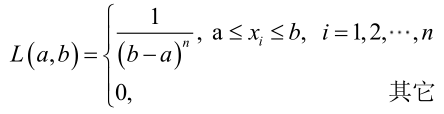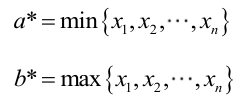最大似然估计（MLE）

在研究语音识别中的算法之前，需要做一些基础理论的介绍，以便更好地进行后面的算法学习！~~~本文主要研究极大似然估计的理论。

下面由经典的贝叶斯分类决策来引入极大似然估计：

贝叶斯公式：

                                            

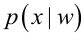
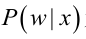
其中：p(w)：为先验概率，表示每种类别分布的概率；：类条件概率，表示在某种类别前提下，某事发生的概率；而为后验概率，表示某事发生了，并且它属于某一类别的概率，通过后验概率，我们就可以对样本进行分类。后验概率越大，说明某X属于这个类别W的可能性越大，我们越有理由把它归到这个类别W下，贝叶斯分类决策很普遍也很容易理解。实例说明如下：

已知，狗蛋儿在下雨天去幼儿园的概率是1/2，在晴天去幼儿园的概率是2/3，下雨天与晴天的比例是2:1，那么问题来了，狗蛋儿今天去幼儿园了，问今天是下雨还是晴天？

从问题可以看出， 事件发生了，我们要求出后验概率，根据贝叶斯公式求解步骤如下：

设：                                    W1：下雨；W2 ：晴天； X：去幼儿园；

由已知条件可知：

                                

狗蛋下雨天或者晴天去幼儿园是相互独立的，由此可以算出

                          

继而由贝叶斯公式可以求得后验概率，也就是狗蛋去去幼儿园的条件下，当天天气是下雨天和晴天的概率：

                          

那么问题又来了：如果我们不知道先验概率和类条件概率，我们只有狗蛋儿以前去幼儿园的一些样本，如何根据仅有的样本来识别以后狗蛋去幼儿园的天气情况（后验概率）呢，最直接的方法就是找到（估计）和，根据估计值，再套用贝叶斯公式进行计算。

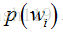
先验概率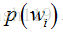的估计比较容易：1，根据已知知识和经验；2，根据样本进行统计（样本要足够的全）

类条件概率就比较难了：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是，把估计完全未知的概率密度转化为估计参数。这里就将概率密度估计问题转化为参数估计问题，极大似然估计就是一种参数估计方法。当然了，概率密度函数的选取很重要，模型正确，在样本区域无穷时，我们会得到较准确的估计值，如果模型都错了，本来是高斯模型的概率密度函数，我们以为是均匀分布模型，那估计半天的参数，肯定也没啥意义了。

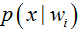
最终，最大似然估计的目的就是根据样本，来估计出概率密度函数的参数值。

Maximum Likehood Estimation

原理：最大似然估计是建立在最大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“ 模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为最大似然估计。

在估计开始前时，我们对样本有一个重要的要求：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，且有充分的训练样本。

由于样本集中的样本都是独立同分布，可以只考虑一类样本集D，来估计参数向量θ。记已知的样本集为：

                                                

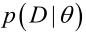
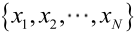
似然函数（linkehood function）：联合概率密度函数称为相对于的θ的似然函数。

                 

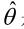
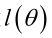
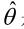
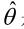
如果是参数空间中能使似然函数最大的θ值，则应该是“最可能”的参数值，那么就是θ的极大似然估计量。它是样本集的函数，记作：

                               

求最大似然函数

    最大似然估计：求使得出现该组样本的概率最大的θ值。

                             

    实际中为了便于分析，定义了对数似然函数：

                                                 

         

 1. 未知参数只有一个（θ为标量）

    在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：

                           

2.未知参数有多个（θ为向量）

    则θ可表示为具有S个分量的未知向量：

                                                      

    记梯度算子：

                                            

若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。

                        

方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。

结合两个常用模型进行直观求解：

    例1：设样本服从正态分布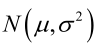，则似然函数为：

        它的对数：

        求导，得方程组：

        联合解得：

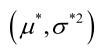
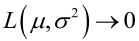
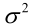
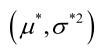
        似然方程有唯一解：，而且它一定是最大值点，这是因为当或时，非负函数。于是U和的极大似然估计为。

        例2：设样本服从均匀分布[a, b]。则X的概率密度函数：

        对样本：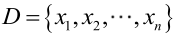

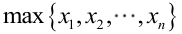
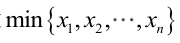
        很显然，L(a,b)作为a和b的二元函数是不连续的，这时不能用导数来求解。而必须从极大似然估计的定义出发，求L(a,b)的最大值，为使L(a,b)达到最大，b-a应该尽可能地小，但b又不能小于，否则，L(a,b)=0。类似地a不能大过，因此，a和b的极大似然估计：

求最大似然估计量的一般步骤：

        （1）写出似然函数；

        （2）对似然函数取对数，并整理；

        （3）求导数；

        （4）解似然方程。

        最大似然估计的特点：

        1.比其他估计方法更加简单；

        2.收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；

        3.如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计结果。

顺便说一下似然函数和条件概率密度函数：

p(x|θ)，表示在θ发生的条件下x的概率； 
p(x;θ)，表示给定x，关于未知参数θ的函数，即似然函数L(θ)。 
也就是说，p(x|θ)是固定θ关于x的函数；p(x;θ)表示给定x，关于θ的函数。两者想要表达的意义不是一样的，但在独立同分布模型中，两者的数值是相等的！~~~可以说求得似然函数的最大值，就是条件概率的最大值。