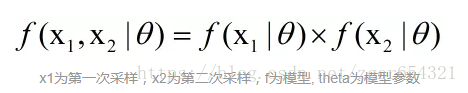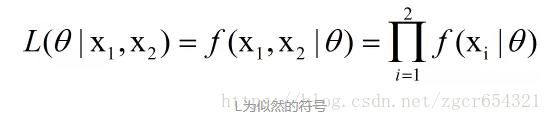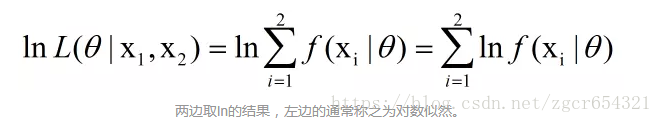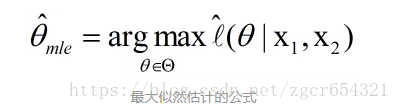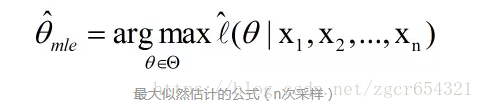什么是似然：
“似然”用通俗的话来说就是可能性，极大似然就是最大的可能性。
似然函数：
似然函数是一种关于统计模型中的参数的函数，表示模型参数中的似然性。似然函数在统计推断中有重大作用，如最大似然估计等。“似然性”与“概率”的意义相近，都是指某种事件发生的可能性，但是在统计学中，“似然性”和“或然性”或“概率”又有明确的区分。
概率用于在已知一些参数的情况下，预测接下来的观测所得到的结果，而似然性则是用于在已知某些观测所得到的结果时，对有关事物的性质的参数进行估计。
如：
对“一枚正反对称的硬币上抛十次”这种事件，我们可以问硬币落地时十次都是正面向上的“概率”是多少；
对“一枚硬币上抛十次，有十次是正面”，我们则可以问，这枚硬币正反面对称的“似然”程度是多少。
条件概率：
是指事件A在另外一个事件B已经发生条件下的发生概率。表示为：P(A|B)，读作“在B的条件下A发生的概率”。
若只有两个事件A、B，设A、B两事件的发生概率为P(A)、P(B)。
则：
P(A|B)=P(AB)/P(B)
如：
假如有一同学，考试成绩数学不及格的概率是0.15，语文不及格的概率是0.05，两者都不及格的概率为0.03，在一次考试中，已知他数学不及格，那么他语文不及格的概率是多少？
我们记事件A为“数学不及格”，事件B为“语文不及格”,则
P(A)=0.15
P(B)=0.05
P(AB)=0.03
已知他数学不及格，那么他语文不及格的概率即已知事件A发生条件下B发生的概率：
P(B|A)=P(AB)/P(A)=0.2
贝叶斯定理：
贝叶斯公式又被称为贝叶斯定理。所谓贝叶斯公式，是指当分析样本大到接近总体数时，样本中事件发生的概率将接近于总体中事件发生的概率。
贝叶斯定理可以用来描述两个条件概率之间的关系，比如 P(A|B) 和 P(B|A)。
按照乘法法则（其实就是条件概率公式的变形）
P(AB) = P(A)*P(B|A)=P(B)*P(A|B)
我们可以得到P(A|B) 和 P(B|A)的关系
P(B|A) = P(A|B)*P(B) / P(A)，这就是贝叶斯定理。
似然函数可以理解为条件概率的逆反：
在已知某个参数B时，事件A会发生的概率写作：
P(A|B)=P(AB)/P(B)
我们可以反过来构造表示似然性的方法：
已知有事件A发生，运用似然函数L(B|A)，估计参数B的可能性。
在形式上，似然函数也是一种条件概率函数，但我们关注的变量改变了：
注意这里并不要求似然函数满足归一性
一个似然函数乘以一个正的常数之后仍然是似然函数。对所有
最大似然估计（maximum likelihood estimation ，MLE）：
给定一个概率分布
，已知其概率密度函数（连续分布）或概率质量函数（离散分布）
，但我们不知道
的值，只知道这个分布中抽出的具有n个值的采样
，我们这n个值的采样数据来估计
。求得一个关于
最大似然估计会寻找基于我们的n个值的采样数据得到的关于
最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的。
多元函数取得极值的条件：
定理1（必要条件）：
设函数z=f(x,y)在点(x0,y0)有偏导数，且在点(x0,y0)处有极值，则它的该点的所有偏导数必然为0。即fx(x0,y0)=0，fy(x0,y0)=0
A的充分条件是B，即A是B的必要条件 ：推理关系B可以推出A，A不能推出B。
为什么是必要条件：
极值点不一定可微、可导，偏导数不一定存在。可微函数极值点，一阶偏导数必为0。
定理2（充分条件）：
设函数z=f(x,y)在点(x0,y0)的某邻域内连续且有一阶和二阶连续偏导数，又fx(x0,y0)=0，fy(x0,y0)=0，令fxx(x0,y0)=A，fxy(x0,y0)=B，fyy(x0,y0)=C，则f(x,y)在点(x0,y0)处是否取得极值的条件如下：
（1）
时有极值，且A<0时有极大值，A>0时有极小值；
（2）
时没有极值；
（3）
时可能有极值，也可能没有极值。
利用上面多元函数取得极值的条件的定理1（必要条件），极大似然估计法的具体做法如下：
1、根据总体的分布，建立似然函数L（此时的theta1-thetak为变量，是未知的）：
2、当似然函数L关于 
可微时，令
，这个方程组就是似然方程。当所有的theta_i的一阶偏导数等于0时，这个似然函数就可以取到最大值（即求L(thetai)这个多元函数的极值点
）。似然函数L取得极值时即可能性最大。所以要求出这个似然方程的解。
3、因为L与lnL有相同的极大值点，且对数函数好求导，所以也可以由方程组
求得，这个方程称为对数似然方程。
4、
就是我们所求的参数
的极大似然估计量。
5、当总体是离散型的，则将上面的概率密度函数
换成它的分布律
。
注意：
上面这句话的通俗说法是：theta1-thetak是一组概率，这些概率是有真实值的，但是我们在目前条件下无法求出。所以我们列一个似然函数L(thetai)，这个函数是一个多元函数，有多个自变量thetai，如果这个函数L是可微的，根据多元函数取得极值的条件的定理1，我们求出满足函数L的所有一阶偏导数等于0的一组thetai的值，这就是可能的极值点。在出题中，这些点往往只有一个或很容易排除掉其他的候选点。
这组thetai的值代表：
我们不知道在总体样本下的thetai的真实值，因此我们使用一组采样得到的n个真实样本值带入L(thetai)函数，然后求得其极值点，这时求得的一组thetai的值就是基于这n个采样的样本值时我们认为这一组thetai的最有可能取的值。
一个帮助理解的例子：
假设有甲乙两支足球队要进行比赛，某人分析这两个球队的资料，得出甲队战胜乙队的概率为p。但是第二天被朋友问及此事时，此人忘记了这个概率p。他只知道甲队战胜乙队的概率p只可能取如下几个值：0，0.1，0.3，0.5，0.75，0.9，但不知道是哪一个。
于是他开始查找这两个球队某日的比赛中的结果，发现是平局，于是他认为这五个概率中0.5是最像的。
如果他发现是甲队赢了乙队，那么他认为此时这五个概率中0.9是最像的。
如果我们从“最大似然”的原文maximum likelihood来看，就会发现这个名称的原始含义就是“最大可能性（看起来最像）”的意思。最大似然的可能性判定是根据已知的一个抽样的小样本（如上个例子中某日的一场比赛的结果）来的。
数学例子1：
假设一个袋子装有白球与红球，比例未知，现在抽取10次（每次抽完都放回，保证事件独立性），假设抽到了7次白球和3次红球，在此数据样本条件下，可以采用最大似然估计法求解袋子中白球的比例（最大似然估计是一种“模型已定，参数未知”的方法）。
当然，这种数据情况下很明显，白球的比例是70%。
我们可以定义从袋子中抽取白球和红球的概率如下：
其中theta是未知的，因此，我们定义似然函数L为：
两边取ln，取ln是为了将右边的乘号变为加号，方便求导。
再除以采样次数，就是平均对数似然：
最大似然估计的过程，就是找一个合适的theta，使得平均对数似然的值为最大。因此，可以得到以下公式：
当然也可以拓展到多次采样的情况：
我们定义M为模型（也就是之前公式中的f，似然函数的L），表示抽到白球的概率为theta，而抽到红球的概率为(1-theta)，因此10次抽取抽到白球7次的概率可以表示为：
其平均似然为：
最大似然就是找到一个合适的theta，获得最大的平均似然。因此我们可以对平均似然的公式对theta求导，并令导数为0。
当抽取白球的概率为0.7时，最可能产生10次抽取抽到白球7次的事件。
由于这个例子比较简单，只有theta1和theta2，且theta2可以用theta1表示，所以似然函数L变为一元函数，我们只需要令其导数为0，就可以求得一元函数L的极值点，这个极值点的x值就是所求的theta。
数学例子2：
已知X是离散型随机变量，可能的取值有0，1, 2。对应概率为：
我们对X抽取容量为10的样本，其中有2个0、5个1、3个2，求θ的最大似然估计值。
1、写出似然函数：
2、对似然函数取对数：
3、对对数似然函数求导，并令导函数为0，这里只有一个theta，所以就不是求偏导了：
4、解上面这个似然方程，最后得到θ的最大似然估计值为9/20。