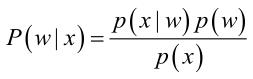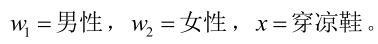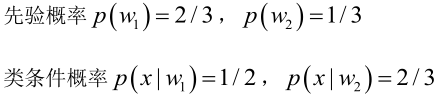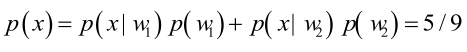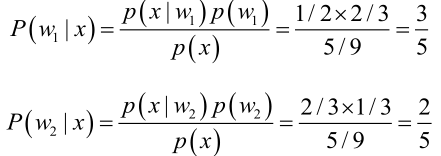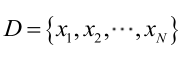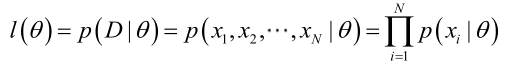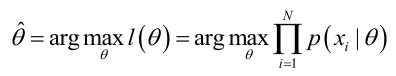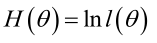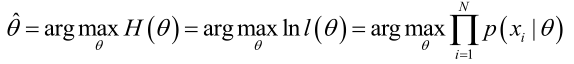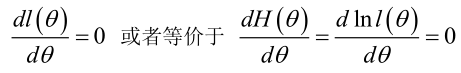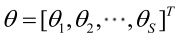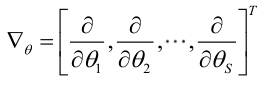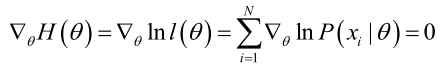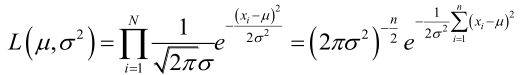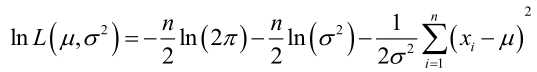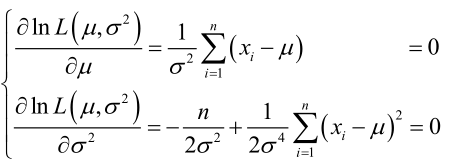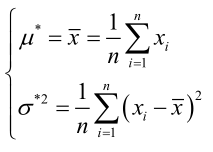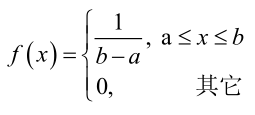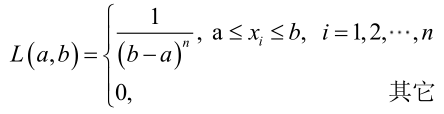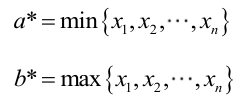贝叶斯决策
首先来看贝叶斯分类，我们都知道经典的贝叶斯公式：
其中：p(w)：为先验概率，表示每种类别分布的概率；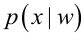
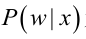
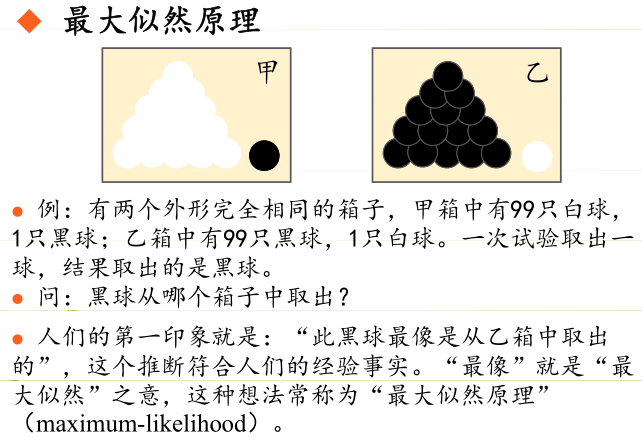
我们来看一个直观的例子：已知：在夏季，某公园男性穿凉鞋的概率为1/2，女性穿凉鞋的概率为2/3，并且该公园中男女比例通常为2:1，问题：若你在公园中随机遇到一个穿凉鞋的人，请问他的性别为男性或女性的概率分别为多少？
从问题看，就是上面讲的，某事发生了，它属于某一类别的概率是多少？即后验概率。
设：
由已知可得：
男性和女性穿凉鞋相互独立，所以
（若只考虑分类问题，只需要比较后验概率的大小，的取值并不重要）。
由贝叶斯公式算出：
问题引出：但是在实际问题中并不都是这样幸运的，我们能获得的数据可能只有有限数目的样本数据，而先验概率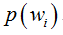
和类条件概率(各类的总体分布)
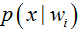都是未知的。根据仅有的样本数据进行分类时，一种可行的办法是我们需要先对先验概率和类条件概率进行估计，然后再套用贝叶斯分类器。
先验概率的估计较简单，1、每个样本所属的自然状态都是已知的（有监督学习）；2、依靠经验；3、用训练样本中各类出现的频率估计。
类条件概率的估计（非常难），原因包括：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。
解决的办法就是，把估计完全未知的概率密度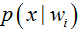
重要前提
上面说到，参数估计问题只是实际问题求解过程中的一种简化方法（由于直接估计类条件概率密度函数很困难）。所以能够使用极大似然估计方法的样本必须需要满足一些前提假设。
重要前提：训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件)，且有充分的训练样本。
极大似然估计
极大似然估计的原理，用一张图片来说明，如下图所示：
总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。
原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。
由于样本集中的样本都是独立同分布，可以只考虑一类样本集D，来估计参数向量θ。记已知的样本集为：
似然函数（linkehood function）：联合概率密度函数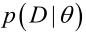
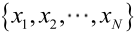
如果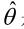
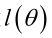
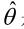
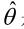
求解极大似然函数
ML估计：求使得出现该组样本的概率最大的θ值。
实际中为了便于分析，定义了对数似然函数：
1. 未知参数只有一个（θ为标量）
在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：
2.未知参数有多个（θ为向量）
则θ可表示为具有S个分量的未知向量：
记梯度算子：
若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。
方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。
极大似然估计的例子
例1：设样本服从正态分布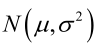
它的对数：
求导，得方程组：
联合解得：
似然方程有唯一解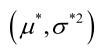
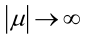
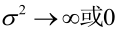
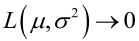
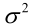
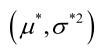
例2：设样本服从均匀分布[a, b]。则X的概率密度函数：
对样本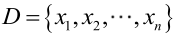
很显然，L(a,b)作为a和b的二元函数是不连续的，这时不能用导数来求解。而必须从极大似然估计的定义出发，求L(a,b)的最大值，为使L(a,b)达到最大，b-a应该尽可能地小，但b又不能小于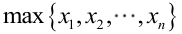
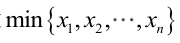
总结
求最大似然估计量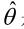
（1）写出似然函数；
（2）对似然函数取对数，并整理；
（3）求导数；
（4）解似然方程。
最大似然估计的特点：
1.比其他估计方法更加简单；
2.收敛性：无偏或者渐近无偏，当样本数目增加时，收敛性质会更好；
3.如果假设的类条件概率模型正确，则通常能获得较好的结果。但如果假设模型出现偏差，将导致非常差的估计结果。
% 二维正态分布的两分类问题 （ML估计） clc; clear; % 两个类别数据的均值向量 Mu = [0 0; 3 3]'; % 协方差矩阵 S1 = 0.8 * eye(2); S(:, :, 1) = S1; S(:, :, 2) = S1; % 先验概率（类别分布） P = [1/3 2/3]'; % 样本数据规模 % 收敛性：无偏或者渐进无偏，当样本数目增加时，收敛性质会更好 N = 500; % 1.生成训练和测试数据 %{ 生成训练样本 N = 500, c = 2, d = 2 μ1=[0, 0]' μ2=[3, 3]' S1=S2=[0.8, 0; 0.8, 0] p(w1)=1/3 p(w2)=2/3 %} randn('seed', 0); [X_train, Y_train] = generate_gauss_classes(Mu, S, P, N); figure(); hold on; class1_data = X_train(:, Y_train==1); class2_data = X_train(:, Y_train==2); plot(class1_data(1, :), class1_data(2, :), 'r.'); plot(class2_data(1, :), class2_data(2, :), 'g.'); grid on; title('训练样本'); xlabel('N=500'); %{ 用同样的方法生成测试样本 N = 500, c = 2, d = 2 μ1=[0, 0]' μ2=[3, 3]' S1=S2=[0.8, 0; 0.8, 0] p(w1)=1/3 p(w2)=2/3 %} randn('seed', 100); [X_test, Y_test] = generate_gauss_classes(Mu, S, P, N); figure(); hold on; test1_data = X_test(:, Y_test==1); test2_data = X_test(:, Y_test==2); plot(test1_data(1, :), test1_data(2, :), 'r.'); plot(test2_data(1, :), test2_data(2, :), 'g.'); grid on; title('测试样本'); xlabel('N=500'); % 2.用训练样本采用ML方法估计参数 % 各类样本只包含本类分布的信息，也就是说不同类别的参数在函数上是独立的 [mu1_hat, s1_hat] = gaussian_ML_estimate(class1_data); [mu2_hat, s2_hat] = gaussian_ML_estimate(class2_data); mu_hat = [mu1_hat, mu2_hat]; s_hat = (1/2) * (s1_hat + s2_hat); % 3.用测试样本和估计出的参数进行分类 % 使用欧式距离进行分类 z_euclidean = euclidean_classifier(mu_hat, X_test); % 使用贝叶斯方法进行分类 z_bayesian = bayes_classifier(Mu, S, P, X_test); % 4.计算不同方法分类的误差 err_euclidean = ( 1-length(find(Y_test == z_euclidean')) / length(Y_test) ); err_bayesian = ( 1-length(find(Y_test == z_bayesian')) / length(Y_test) ); % 输出信息 disp(['基于欧式距离分类的误分率：', num2str(err_euclidean)]); disp(['基于最小错误率贝叶斯分类的误分率：', num2str(err_bayesian)]); % 画图展示 figure(); hold on; z_euclidean = transpose(z_euclidean); o = 1; q = 1; for i = 1:size(X_test, 2) if Y_test(i) ~= z_euclidean(i) plot(X_test(1,i), X_test(2,i), 'bo'); elseif z_euclidean(i)==1 euclidean_classifier_results1(:, o) = X_test(:, i); o = o+1; elseif z_euclidean(i)==2 euclidean_classifier_results2(:, q) = X_test(:, i); q = q+1; end end plot(euclidean_classifier_results1(1, :), euclidean_classifier_results1(2, :), 'r.'); plot(euclidean_classifier_results2(1, :), euclidean_classifier_results2(2, :), 'g.'); title(['基于欧式距离分类，误分率为：', num2str(err_euclidean)]); grid on; figure(); hold on; z_bayesian = transpose(z_bayesian); o = 1; q = 1; for i = 1:size(X_test, 2) if Y_test(i) ~= z_bayesian(i) plot(X_test(1,i), X_test(2,i), 'bo'); elseif z_bayesian(i)==1 bayesian_classifier_results1(:, o) = X_test(:, i); o = o+1; elseif z_bayesian(i)==2 bayesian_classifier_results2(:, q) = X_test(:, i); q = q+1; end end plot(bayesian_classifier_results1(1, :), bayesian_classifier_results1(2, :), 'r.'); plot(bayesian_classifier_results2(1, :), bayesian_classifier_results2(2, :), 'g.'); title(['基于最小错误率的贝叶斯决策分类，误分率为：', num2str(err_bayesian)]); grid on;
生成数据的函数：
function [ data, C ] = generate_gauss_classes( M, S, P, N )
%{
函数功能：
生成样本数据，符合正态分布
参数说明：
M：数据的均值向量
S：数据的协方差矩阵
P：各类样本的先验概率，即类别分布
N：样本规模
函数返回
data：样本数据（2*N维矩阵）
C：样本数据的类别信息
%}
[~, c] = size(M);
data = [];
C = [];
for j = 1:c
% z = mvnrnd(mu,sigma,n);
% 产生多维正态随机数，mu为期望向量，sigma为协方差矩阵，n为规模。
% fix 函数向零方向取整
t = mvnrnd(M(:,j), S(:,:,j), fix(P(j)*N))';
data = [data t];
C = [C ones(1, fix(P(j) * N)) * j];
end
end
正态分布的ML估计（对训练样本）：
function [ m_hat, s_hat ] = gaussian_ML_estimate( X )
%{
函数功能：
样本正态分布的最大似然估计
参数说明：
X：训练样本
函数返回：
m_hat：样本由极大似然估计得出的正态分布参数，均值
s_hat：样本由极大似然估计得出的正态分布参数，方差
%}
% 样本规模
[~, N] = size(X);
% 正态分布样本总体的未知均值μ的极大似然估计就是训练样本的算术平均
m_hat = (1/N) * sum(transpose(X))';
% 正态分布中的协方差阵Σ的最大似然估计量等于N个矩阵的算术平均值
s_hat = zeros(1);
for k = 1:N
s_hat = s_hat + (X(:, k)-m_hat) * (X(:, k)-m_hat)';
end
s_hat = (1/N)*s_hat;
end
% 详细的计算过程推导可以参考前一篇博客：极大似然估计详解。
有了估计参数，对测试数据进行分类：
基于欧式距离的分类：
function [ z ] = euclidean_classifier( m, X )
%{
函数功能：
利用欧式距离对测试数据进行分类
参数说明：
m：数据的均值，由ML对训练数据，参数估计得到
X：我们需要测试的数据
函数返回：
z：数据所属的分类
%}
[~, c] = size(m);
[~, n] = size(X);
z = zeros(n, 1);
de = zeros(c, 1);
for i = 1:n
for j = 1:c
de(j) = sqrt( (X(:,i)-m(:,j))' * (X(:,i)-m(:,j)) );
end
[~, z(i)] = min(de);
end
end
基于最小错误率的贝叶斯估计：
function [ z ] = bayes_classifier( m, S, P, X )
%{
函数功能：
利用基于最小错误率的贝叶斯对测试数据进行分类
参数说明：
m：数据的均值
S：数据的协方差
P：数据类别分布概率
X：我们需要测试的数据
函数返回：
z：数据所属的分类
%}
[~, c] = size(m);
[~, n] = size(X);
z = zeros(n, 1);
t = zeros(c, 1);
for i = 1:n
for j = 1:c
t(j) = P(j) * comp_gauss_dens_val( m(:,j), S(:,:,j), X(:,i) );
end
[~, z(i)] = max(t);
end
end
function [ z ] = comp_gauss_dens_val( m, s, x )
%{
函数功能：
计算高斯分布N（m, s），在某一个特定点的值
参数说明：
m：数据的均值
s：数据的协方差
x：我们需要计算的数据点
函数返回：
z：高斯分布在x出的值
%}
z = ( 1/( (2*pi)^(1/2)*det(s)^0.5 ) ) * exp( -0.5*(x-m)'*inv(s)*(x-m) );
end