似然函数与最大似然估计、交叉熵概念与机器学习中的交叉熵函数

版权声明：站在巨人的肩膀上学习。 https://blog.csdn.net/zgcr654321/article/details/85204049

似然函数与最大似然估计

似然的概念

“似然”用通俗的话来说就是可能性，极大似然就是最大的可能性。

似然函数

似然函数是关于统计模型中的一组概率的函数(这些概率的真实值我们并不知道)，似然函数的因变量值表示了模型中的概率参数的似然性(可能性)。

最大似然估计

我们列出似然函数后，从真实事件中取得一批n个采样样本数据，最大似然估计会寻找基于我们的n个值的采样数据得到的关于的最可能的值（即，在所有可能的取值中，寻找一个值使这n个值的采样数据的“可能性”最大化）。

最大似然估计中采样需满足一个很重要的假设，就是所有的采样都是独立同分布的。

伯努利分布

伯努利分布(Bernoulli distribution)又名两点分布或0-1分布，介绍伯努利分布前首先需要引入伯努利试验（Bernoulli trial）。

伯努利试验是只有两种可能结果的单次随机试验，即对于一个随机变量X而言：

$P ( X = 1 ) = p$
$P ( X = 0 ) = 1 - p$

伯努利试验可以表达为“是或否”的问题。

如果试验E是一个伯努利试验，将E独立重复地进行n次，则称这一串重复的独立试验为n重伯努利试验。

进行一次伯努利试验，成功(X=1)概率为p(0<=p<=1)，失败(X=0)概率为1-p，则称随机变量X服从伯努利分布。

其概率质量函数为：

$f ( x ) = p ^ { x } ( 1 - p ) ^ { 1 - x } = \left\{ \begin{array} { l l } { p } &amp; { \text { if } x = 1 } \\ { 1 - p } &amp; { \text { if } x = 0 } \\ { 0 } &amp; { \text { otherwise } } \end{array} \right.$

伯努利分布的 $EX = p , DX = p ( 1 - p )$。伯努利分布是一个离散型机率分布，是N=1时二项分布的特殊情况。

伯努利分布下的最大似然估计

假设 $P ( X = 1 ) = p , P ( X = 0 ) = 1 - p$，则有

$P ( X ) = p ^ { X } ( 1 - p ) ^ { 1 - X }$

假设我们现在有一组采样得到的数据D，则其对数似然函数为

$\begin{aligned} \max _ { p } \log P ( D ) &amp; = \max _ { p } \log \prod _ { i } ^ { N } P \left( D _ { i } \right) \\ &amp; = \max _ { p } \sum _ { i } \log P \left( D _ { i } \right) \\ &amp; = \max _ { p } \sum _ { i } \left[ D _ { i } \log p + \left( 1 - D _ { i } \right) \log ( 1 - p ) \right] \end{aligned}$

现在我们来求其极大似然估计，即求对数似然函数取极大值时函数的自变量的取值。

将上式对P求导可得：

$\nabla _ { p } \max _ { p } \log P ( D ) = \sum _ { i } ^ { N } \left[ D _ { i } \frac { 1 } { p } + \left( 1 - D _ { i } \right) \frac { 1 } { p - 1 } \right]$

令导数为0，则有：

$\sum _ { i } ^ { N } \left[ D _ { i } \frac { 1 } { p } + \left( 1 - D _ { i } \right) \frac { 1 } { p - 1 } \right] = 0$

消去分母，得：

\sum _ { i } ^ { N } \left[ D _ { i } ( p - 1 ) + \left( 1 - D _ { i } \right) p \right] = 0

于是可得：

$\sum _ { i } ^ { N } \left( p - D _ { i } \right) = 0$

$p = \frac { 1 } { N } \sum _ { i } D _ { i }$

这就是伯努利分布下最大似然估计求出的结果。

高斯分布

其实就是正态分布（Normal distribution），又叫高斯分布。

若随机变量X服从一个数学期望为 $\mu$、方差为 $\sigma ^ { 2 }$的正态分布，记为 $X \sim N \left( \mu , \sigma ^ { 2 } \right)$。其概率密度函数为：

$f ( x ) = \frac { 1 } { \sigma \sqrt { 2 \pi } } e ^ { - \frac { ( x - \mu ) ^ { 2 } } { 2 \sigma ^ { 2 } } }$

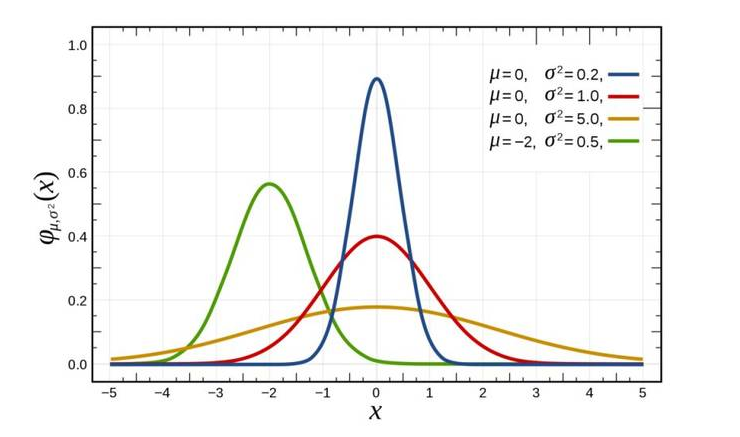
正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。下图中红色曲线就是标准正态分布。

高斯分布下的最大似然估计

我们已经知道高斯分布的概率密度函数为：

$f ( x ) = \frac { 1 } { \sqrt { 2 \pi \sigma ^ { 2 } } } e ^ { - \frac { ( x - \mu ) ^ { 2 } } { 2 \sigma ^ { 2 } } }$

那么其对数似然函数为：

$\begin{aligned} \max \log P ( D ) &amp; = \max _ { p } \log \prod _ { i } P \left( D _ { i } \right) \\ &amp; = \max \sum _ { i } ^ { N } \log P \left( D _ { i } \right) \\ &amp; = \max \sum _ { i } ^ { N } \left[ - \frac { 1 } { 2 } \log \left( 2 \pi \sigma ^ { 2 } \right) - \frac { \left( D _ { i } - \mu \right) ^ { 2 } } { 2 \sigma ^ { 2 } } \right] \\ &amp; = \max \left[ - \frac { N } { 2 } \log \left( 2 \pi \sigma ^ { 2 } \right) - \frac { 1 } { 2 \sigma ^ { 2 } } \sum _ { i } ^ { N } \left( D _ { i } - \mu \right) ^ { 2 } \right] \end{aligned}$

现在我们来求其极大似然估计，即求对数似然函数取极大值时函数的自变量的取值。

将上式对 $\mu$求导，并令导数为0，可得：

$\frac { \partial \max _ { \mu } \log P ( D ) } { \partial \mu } = - \frac { 1 } { \sigma ^ { 2 } } \sum _ { i } ^ { N } \left( \mu - D _ { i } \right) = 0$

于是我们可得：

$\mu = \frac { 1 } { N } \sum _ { i } ^ { N } D _ { i }$

上式再对 $\sigma ^ { 2 }$求导，并令导数为0，可得：

$\frac { \partial \max _ { \sigma ^ { 2 } } \log P ( D ) } { \partial \sigma ^ { 2 } } = - \frac { N } { 2 \sigma ^ { 2 } } + \frac { 1 } { 2 \sigma ^ { 4 } } \sum _ { i } ^ { N } \left( D _ { i } - \mu \right) ^ { 2 } = 0$

于是我们可得：

$\sigma ^ { 2 } = \frac { 1 } { N } \sum _ { i } ^ { N } \left( D _ { i } - \mu \right) ^ { 2 }$

信息量、熵、相对熵、交叉熵、机器学习中的交叉熵函数

信息量

假设X是一个离散型随机变量，其取值集合为X，概率分布函数为 $p ( x ) = \operatorname { Pr } ( X = x ) , x \in X$，我们定义事件 $X = x_{0}$的信息量为：

$I \left( x _ { 0 } \right) = - \log \left( p \left( x _ { 0 } \right) \right)$

一个事件发生的概率越大，则它所携带的信息量就越小，而当 $p ( x_{0} ) = 1$时，熵将等于0，也就是说该事件的发生不会导致任何信息量的增加。

如：

小明平时不爱学习，考试经常不及格，而小王是个勤奋学习的好学生，经常得满分，所以我们可以做如下假设：

事件A：小明考试及格，对应的概率 $P ( x_{A} ) = 0.1$，信息量为 $I ( x_{A} ) = - \log ( 0.1 ) = 3.3219$
事件B：小王考试及格，对应的概率 $P ( x_{A} ) = 0.999$，信息量为 $I ( x_{B} ) = - \log ( 0.999 ) = 0.0014$

上面的结果可以看出，小明及格的可能性很低(十次考试只有一次及格)，因此如果某次考试及格了，必然会引入较大的信息量，对应的I值也较高。而对于小王而言，考试及格是大概率事件，在事件B发生前，大家普遍认为事件B的发生几乎是确定的，因此当某次考试小王及格这个事件发生时并不会引入太多的信息量，相应的I值也非常的低。

熵

还是通过上边的例子来说明，假设小明的考试结果是一个0-1分布 $X_{A}$，只有两个取值{0：不及格，1：及格}。

在某次考试结果公布前，小明的考试结果有多大的不确定度呢？

你肯定会说：十有八九不及格！因为根据先验知识，小明及格的概率仅有0.1，90%的可能都是不及格的。

怎么来度量这个不确定度？

我们对所有可能结果带来的额外信息量求取均值（期望），其结果就能够衡量出小明考试成绩的不确定度。

即：

$\mathrm { H_{A} } ( \mathrm { x } ) = - [ \mathrm { p } ( \mathrm { x_{A} } ) \log ( \mathrm { p } ( \mathrm { x_{A} } ) ) + ( 1 - \mathrm { p } ( \mathrm x_{A} ) ) \log ( 1 - \mathrm { p } ( \mathrm { x_{A} } ) ) ] = 0.4690$

小王的熵为：

$\mathrm { H_{B} } ( \mathrm { x } ) = - [ p ( x_{B}) \log ( p (x_{B}) ) + ( 1 - p ( x_{B}) ) \log ( 1 - p ( x_{B}) ) ] = 0.0114$

虽然小明考试结果的不确定性较低，毕竟十次有9次都不及格，但是也比不上小王（1000次考试只有一次才可能不及格，结果相当的确定） 。

我们再假设一个成绩相对普通的学生小东，他及格的概率是P(xC)=0.5，即及格与否的概率是一样的，则他的熵为：

$\mathrm { H_{C} } ( \mathrm { x } )= - [ p ( x_{C} ) \log ( p ( x_{C} ) ) + ( 1 - p ( x_{C} ) ) \log ( 1 - p ( x_{C} ) ) ] = 1$

其熵为1，也就是说他的不确定性比前边两位同学要高很多，在成绩公布之前，很难准确猜测出他的考试结果。

从上面可以看出，熵其实是信息量的期望值，它是一个随机变量的确定性的度量。熵越大，变量的取值越不确定，反之就越确定。

对于一个随机变量X而言，它的所有可能取值的信息量的期望 $E [I( x ) ]$就称为熵。

X的熵定义为：

$H ( X ) = E _ { p } \log \frac { 1 } { p ( x ) } = - \sum _ { x \in X } p ( x ) \log p ( x )$

如果p(x)是连续型随机变量，则熵定义为：

$H ( X ) = - \int _ { x \in X } p ( x ) \log p ( x ) d x$

为保证有效性，这里约定当p(x)→0时,有p(x)logp(x)→0

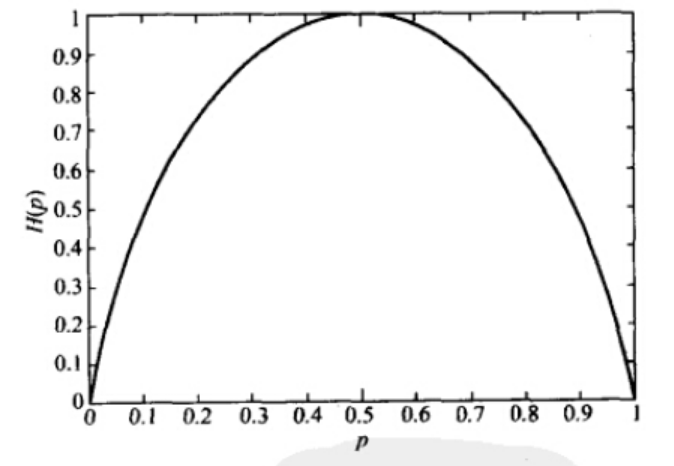
当X为0-1分布时，熵与概率p的关系如下图：

可以看出，当两种取值的可能性相等时，不确定度最大（此时没有任何先验知识），这个结论可以推广到多种取值的情况。

在图中也可以看出，当p=0或1时，熵为0，即此时X完全确定。

熵的单位随着公式中log运算的底数而变化，当底数为2时，单位为“比特”(bit)，底数为e时，单位为“奈特”。

相对熵（KL散度）

相对熵(relative entropy)又称为KL散度（Kullback-Leibler divergence），它是描述两个概率分布P和Q差异的一种方法。记为 $D _ { K L } ( p \| q )$。

它度量当真实分布为p时，假设分布q的无效性。

两个分布越接近，那么KL散度越小；如果越远，散度就会越大。当两个随机分布相同时，它们的相对熵为零。KL散度的结果一定是非负的。

$D _ { K L } ( p \| q ) = E _ { p } \left[ \log \frac { p ( x ) } { q ( x ) } \right] = \sum _ { x \in \mathcal { X } } p ( x ) \log \frac { p ( x ) } { q ( x ) }$
$= \sum _ { x \in \mathcal { X } } [ p ( x ) \log p ( x ) - p ( x ) \log q ( x ) ]$
$= \sum _ { x \in \mathcal { X } } p ( x ) \log p ( x ) - \sum _ { x \in \mathcal { X } } p ( x ) \log q ( x )$
$= - H ( p ) - \sum _ { x \in \mathcal { X } } p ( x ) \log q ( x )$
$= - H ( p ) + E _ { p } [ - \log q ( x ) ]$
$= H _ { p } ( q ) - H ( p )$

为了保证连续性，做如下约定：

$0 \log \frac { 0 } { 0 } = 0 , \quad 0 \log \frac { 0 } { q } = 0 , p \log \frac { p } { 0 } = \infty$

显然，当p=q时,两者之间的相对熵 $D _ { K L } ( p \| q ) = 0$。 $H _ { p } ( q )$表示在p分布下，使用q进行编码需要的bit数，而H§表示对真实分布p所需要的最小编码bit数。

相对熵的含义为：

$D _ { K L } ( p \| q )$表示在真实分布为p的前提下，使用q分布进行编码相对于使用真实分布p进行编码（即最优编码）所多出来的bit数。

KL散度的结果是非负的，证明如下：

$\begin{aligned} \mathrm { KL } ( p \| q ) &amp; = \sum _ { x } p ( x ) \log \frac { p ( x ) } { q ( x ) } \\ &amp; = - \sum _ { x } p ( x ) \log \frac { q ( x ) } { p ( x ) } \end{aligned}$

对数函数是一个上凸函数，故上式：

$\geqslant - \log \left[ \sum _ { x } p ( x ) \frac { q ( x ) } { p ( x ) } \right]$
$= - \log \left[ \sum _ { x } q ( x ) \right]$
$= - \log 1 = 0$

举例：

假设有两个随机变量X1和x2，各自服从一个高斯分布 $N _ { 1 } \left( \mu _ { 1 } , \sigma _ { 1 } ^ { 2 } \right)$和 $N _ { 2 } \left( \mu _ { 2 } , \sigma _ { 2 } ^ { 2 } \right)$，那么这两个分布的KL散度如何计算？

已知高斯分布的概率密度函数为：

$N ( \mu , \sigma ) = \frac { 1 } { \sqrt { 2 \pi \sigma ^ { 2 } } } e ^ { \frac { ( x - \mu ) ^ { 2 } } { 2 \sigma ^ { 2 } } }$

故 $\mathrm { KL } ( p 1 \| p 2 )$等于：

$\begin{aligned} &amp; \int p _ { 1 } ( x ) \log \frac { p _ { 1 } ( x ) } { p _ { 2 } ( x ) } \mathrm { d } x \\ = &amp; \int p _ { 1 } ( x ) \left( \log p _ { 1 } ( x ) - \log p _ { 2 } ( x ) \right) \mathrm { d } x \\ = &amp; \int p _ { 1 } ( x ) \left( \log \frac { 1 } { \sqrt { 2 \pi \sigma _ { 1 } ^ { 2 } } } e ^ { \frac { ( x - \mu ) ^ { 2 } } { 2 \sigma _ { 1 } ^ { 2 } } } - \log \frac { 1 } { \sqrt { 2 \pi \sigma _ { 2 } ^ { 2 } } } e ^ { \frac { \left( x - \mu _ { 2 } \right) ^ { 2 } } { 2 \sigma _ { 2 } ^ { 2 } } ) } \mathrm { d } x \right. \end{aligned}$

$= \int p _ { 1 } ( x ) \left( - \frac { 1 } { 2 } \log 2 \pi - \log \sigma _ { 1 } - \frac { \left( x - \mu _ { 1 } \right) ^ { 2 } } { 2 \sigma _ { 1 } ^ { 2 } } + \frac { 1 } { 2 } \log 2 \pi + \log \sigma _ { 2 } + \frac { \left( x - \mu _ { 2 } \right) ^ { 2 } } { 2 \sigma _ { 2 } ^ { 2 } } \right) \mathrm { d } x$
$= \int p _ { 1 } ( x ) \left( \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } + \left[ \frac { \left( x - \mu _ { 2 } \right) ^ { 2 } } { 2 \sigma _ { 2 } ^ { 2 } } - \frac { \left( x - \mu _ { 1 } \right) ^ { 2 } } { 2 \sigma _ { 1 } ^ { 2 } } \right] \right) \mathrm { d } x$
$= \int \left( \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } \right) p _ { 1 } ( x ) \mathrm { d } x + \int \left( \frac { \left( x - \mu _ { 2 } \right) ^ { 2 } } { 2 \sigma _ { 2 } ^ { 2 } } \right) p _ { 1 } ( x ) \mathrm { d } x - \int \left( \frac { \left( x - \mu _ { 1 } \right) ^ { 2 } } { 2 \sigma _ { 1 } ^ { 2 } } \right) p _ { 1 } ( x ) \mathrm { d } x$

$= \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } + \frac { 1 } { 2 \sigma _ { 2 } ^ { 2 } } \int \left( \left( x - \mu _ { 2 } \right) ^ { 2 } \right) p _ { 1 } ( x ) \mathrm { d } x - \frac { 1 } { 2 \sigma _ { 1 } ^ { 2 } } \int \left( \left( x - \mu _ { 1 } \right) ^ { 2 } \right) p _ { 1 } ( x ) \mathrm { d } x$

最后一步的右边最后一项就是连续型随机变量的方差计算公式。

连续型随机变量的方差计算公式为：

$D ( X ) = \sigma ^ { 2 } = \int _ { - \infty } ^ { \infty } ( x - \mu ) ^ { 2 } f ( x ) d x$

可化简为：

$D ( X ) = \int x ^ { 2 } f ( x ) d x - \mu ^ { 2 } = E \left( X ^ { 2 } \right) - [ E ( X ) ] ^ { 2 }$

证明：

由数学期望的性质得

$D ( X ) = E \left\{ [ X - E ( X ) ] ^ { 2 } \right\} = E \left\{ X ^ { 2 } - 2 X E ( X ) + [ E ( X ) ] ^ { 2 } \right\}$
$= E \left( X ^ { 2 } \right) - 2 E ( X ) E ( X ) + [ E ( X ) ] ^ { 2 } = E \left( X ^ { 2 } \right) - [ E ( X ) ] ^ { 2 }$

所以例子中最后一步的右边最后一项可计算出值为1/2。

故上式等于：

$= \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } + \frac { 1 } { 2 \sigma _ { 2 } ^ { 2 } } \int \left( \left( x - \mu _ { 2 } \right) ^ { 2 } \right) p _ { 1 } ( x ) \mathrm { d } x - \frac { 1 } { 2 }$
$= \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } + \frac { 1 } { 2 \sigma _ { 2 } ^ { 2 } } \int \left( \left( x - \mu _ { 1 } + \mu _ { 1 } - \mu _ { 2 } \right) ^ { 2 } \right) p _ { 1 } ( x ) \mathrm { d } x - \frac { 1 } { 2 }$
$= \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } + \frac { 1 } { 2 \sigma _ { 2 } ^ { 2 } } \left[ \int \left( x - \mu _ { 1 } \right) ^ { 2 } p _ { 1 } ( x ) \mathrm { d } x + \int \left( \mu _ { 1 } - \mu _ { 2 } \right) ^ { 2 } p _ { 1 } ( x ) \mathrm { d } x \right.+ 2 \int \left( x - \mu _ { 1 } \right) \left( \mu _ { 1 } - \mu _ { 2 } \right) p _ { 1 } ( x ) \mathrm { d } x ] - \frac { 1 } { 2 }$

$= \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } + \frac { 1 } { 2 \sigma _ { 2 } ^ { 2 } } \left[ \int \left( x - \mu _ { 1 } \right) ^ { 2 } p _ { 1 } ( x ) \mathrm { d } x + \left( \mu _ { 1 } - \mu _ { 2 } \right) ^ { 2 } \right] - \frac { 1 } { 2 }$
$= \log \frac { \sigma _ { 2 } } { \sigma _ { 1 } } + \frac { \sigma _ { 1 } ^ { 2 } + \left( \mu _ { 1 } - \mu _ { 2 } \right) ^ { 2 } } { 2 \sigma _ { 2 } ^ { 2 } } - \frac { 1 } { 2 }$

如果假设N2是一个 $\mu _ { 2 } = 0 , \sigma _ { 2 } ^ { 2 } = 1$的正态分布，那么N1应该是怎样的分布，才能使KL最小呢？

$\mu _ { 2 } = 0 , \sigma _ { 2 } ^ { 2 } = 1$代入上式，得：

$\mathrm { KL } \left( \mu _ { 1 } , \sigma _ { 1 } \right) = - \log \sigma _ { 1 } + \frac { \sigma _ { 1 } ^ { 2 } + \mu _ { 1 } ^ { 2 } } { 2 } - \frac { 1 } { 2 }$

显然，当 $\mu _ { 1 } = 0 , \sigma _ { 1 } = 1$时，KL最小为0。

交叉熵

交叉熵容易跟相对熵搞混，二者联系紧密，但又有所区别。

假设有两个分布p，q，则它们在给定样本集上的交叉熵定义如下：

$C E H ( p , q ) = E _ { p } [ - \log q ] = - \sum _ { x \in \mathcal { X } } p ( x ) \log q ( x ) = H ( p ) + D _ { K L } ( p \| q )$

可以看出，交叉熵与上一节定义的相对熵仅相差了 $\mathrm { H } ( \mathrm { p } )$。

当p已知时，可以把 $\mathrm { H } ( \mathrm { p } )$看做一个常数，此时交叉熵与KL距离在行为上是等价的，都反映了分布p，q的相似程度。最小化交叉熵等于最小化KL距离。它们都将在p=q时取得最小值H§（p=q时KL距离为0），因此有的工程文献中将最小化KL距离的方法称为Principle of Minimum Cross-Entropy (MCE)或Minxent方法。

特别的，在logistic regression中：

p:真实样本分布，服从参数为p的0-1分布，即 $X \sim B ( 1 , p )$
q:待估计的模型，服从参数为q的0-1分布，即 $X \sim B ( 1 , q )$

则两者的交叉熵为：

$C E H ( p , q )$
$= - \sum _ { x \in \mathcal { X } } \mathbf { p } ( \mathbf { x } ) \log \mathbf { q } ( \mathbf { x } )$
$= - \left[ P _ { p } ( x = 1 ) \log P _ { q } ( x = 1 ) + P _ { p } ( x = 0 ) \log P _ { q } ( x = 0 ) \right]$
$= - [ p \log q + ( 1 - p ) \log ( 1 - q ) ]$
$= - \left[ \mathbf { y } \log \mathbf { h } _ { \theta } ( x ) + ( 1 - \mathbf { y } ) \log \left( 1 - \mathbf { h } _ { \theta } ( x ) \right) \right]$

对所有训练样本取均值得：

$- \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left[ y ^ { ( i ) } \log h _ { \theta } \left( x ^ { ( i ) } \right) + \left( 1 - y ^ { ( i ) } \right) \log \left( 1 - h _ { \theta } \left( x ^ { ( i ) } \right) \right) \right]$

这个结果与通过最大似然估计方法(求对数似然函数的极值)求出来的结果一致。

机器学习中的交叉熵函数

二分类问题的loss函数（输入数据是softmax或sigmoid函数的输出）：

$\operatorname { loss } = - \frac { 1 } { n } \sum [ y \ln a + ( 1 - y ) \ln ( 1 - a ) ]$

多分类问题使用的loss函数（输入数据是softmax或sigmoid函数的输出）：

$loss = - \sum _ { i } y _ { i } \ln a _ { i }$

如果是在tensorflow中，loss函数往往写成下面这两种形式之一：

loss = tf.reduce_mean(- tf.reduce_sum(y * tf.log(pred), 1))

loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=output, labels=Y))

举例：

假如我们的数据集是mnist，这是一个0-9的手写体数字的数据集，如果我们从其中抽出一个图片，总共只有10种可能，即数字0-9。

一般情况下我们每一次训练都是取一个批样本（batch_size）。

我们现在假设batch_size为1，即每次训练只取一个样本。我们将这个批样本输入神经网络中进行计算，最后经过softmax函数或sigmoid函数后得到一个输出数据，这个输出数据是我们预测的这batchsize个图片的标签向量，它代表了我们的神经网络预测的这输入的batchsize个样本的每个图片分别是哪一类图片（具体到mnist数据集里，就是图片是数字0-9中的哪一个）。

预测的标签向量的形式为：

$[ a 0 , a 1 , a 2 , a 3 , a 4 , a 5 , a 6 , a 7 , a 8 , a 9 ]$

我们的真实标签也是一个有着同样元素数量的向量，一般写作：

$[ y 0 , y 1 , y 2 , y 3 , y 4 , y 5 , y 6 , y 7 , y 8 , y 9 ]$

真实标签中除了代表自己是哪个数字的那个下标的元素是1，其他都是0，如[0,0,0,0,0,1,0,0,0,0]代表数字5。

如果我们把一个图片属于数字0-9中的一个看成10个独立事件，其实这个标签向量代表的就是10个独立事件的概率。

而真实标签代表的就是我们抽取的一个样本。这一个样本中必然会发生一个事件，而其他9个事件都不发生。

现在再看看多分类的loss函数：

$loss = - \sum _ { i } y _ { i } \ln a _ { i }$

显然对于mnist问题，我们的loss函数就是i=10时的情况。

为什么有一个负号？

因为ai总是在0到1之间，而yi值不是0就是1，这就导致每一项要么为0，要么是负数。而tensorflow的优化器是向着loss值降低的方向优化的，并且最终目标是loss值尽可能接近0，所以要求loss函数是一个大于0的值。因此我们加一个负号。

在机器学习中，我们通过tensorflow使用梯度下降或其他的优化方法，不断地更新权重参数，最终使得loss函数从一个正值减小到接近0（也就是似然函数从原来的负值逐渐接近0,在这个mnist的例子中显然0是似然函数的极大值）求出一个接近似然函数极大值的点，这就是我们求出的一个接近极大似然估计值的一组ai值。

也就是说，loss函数值越小，求得的ai值代表的概率越有可能是真实概率。

二分类的loss函数也与上面的原理类似。

假如batch_size为100（或大于1的其他数），我们的loss函数又是如何处理的呢？

看看我们在tensorflow中的loss函数变量的定义就知道了：

loss = tf.reduce_mean(- tf.reduce_sum(y * tf.log(pred), 1))

这个loss函数的意思是，yi与对应的ln(ai)相乘后，使用tf.reduce_sum函数将相乘后的这个向量（相乘后的向量形式是shape=(batch_size、10)的张量）按行求和（其实就是求出了每一个样本的loss值）,然后按列求和后求平均值。

也就是说，当输入一批样本时，我们使用tensorflow优化器更新权重的依据是这一批样本的loss值的平均值。然后通过求loss对各个权重的梯度（链式求导法则），再用梯度更新各个权重。