关于似然函数和最大似然估计的详细说明可以看这篇文章：https://blog.csdn.net/zgcr654321/article/details/83382729
二分类情况和多分类情况下的似然函数与最大似然估计：
二分类情况下的似然函数与最大似然估计：
我们知道按照生活中的常识，一个均匀的硬币抛出落在地上，它是正面或者反面的概率是0.5。但是，有很多事物发生的概率我们并不能这样直观的估计到。
如：
假设一个袋子装有白球与红球，但比例未知，现在抽取10次（每次抽完都放回，保证事件独立性），现在我们抽取10次，抽到了7次白球和3次红球。
我们先设是白球的概率为x，则是红球的概率为1-x。
我们抽取10次，抽到了7次白球和3次红球。
根据这10次的结果，我们就可以列出其似然函数：
又似然函数的L(x)值越大，则表明此时对应的x值“可能性越大”，即此时的x值最有可能接近真实分布中的x值（x是一个概率）。
那么在概率论和数理统计中如何求这个x值呢？
我们先把L(x)写成lnL(x)的形式，由于lnL(x)与L(x)相同的极大值点，且对数函数更好求导，所以我们只要对lnL(x)求导，令导数为0反求对应x的值，x就是一个可能的极大值点，事实上，这个点往往只有一个。
对数似然函数：
对lnL(x)求导：
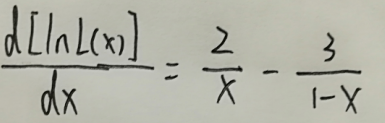
接下来我们令导数为0，得到下式即为对数似然方程：
解这个方程，可得x=0.4。
这个x值就是我们利用这5次抛硬币的结果推测出的最有可能接近抛硬币得到正面的真实概率的概率。
多分类情况下的似然函数与最大似然估计：
假设我们有一个六面体的骰子，骰子扔出后必定有某一个面朝下，而哪个面朝下的概率我们并不知道。
现在我们将骰子扔出15次，其中面1朝下2次，面2朝下3次，面3朝下4次，面4朝下1次，面5朝下2次，面6朝下3次。
我们分别设面1-面6朝下的概率分别为x1、x2、x3、x4、x5、x6。
根据这15次的结果，我们可以列出似然函数：
其对数似然函数：
由于这里的似然函数有多个独立的自变量，所以是对数似然方程组：
当然，这个方程组我们解不出来。
实际上，在概率论与数理统计中，往往多个自变量之间有相互的联系。这使得似然函数最终可以化为只有一个自变量的函数。
例如：
已知X是离散型随机变量，可能的取值有0，1, 2。对应概率为：
我们对X抽取容量为10的样本，其中有2个0、5个1、3个2，求θ的最大似然估计值。
似然函数：
对数似然函数：
对对数似然函数求导，并令导数为0，解θ：
得到θ的最大似然估计值为9/20。
那么二分类的似然函数和多分类的似然函数与机器学习中的交叉熵函数又有什么关系呢？
机器学习中的交叉熵函数：
什么是信息量？
假设X是一个离散型随机变量，其取值集合为X，概率分布函数为p(x)=Pr(X=x),x∈X，我们定义事件X=x0的信息量为：
可以理解为，一个事件发生的概率越大，则它所携带的信息量就越小，而当p(x0)=1时，熵将等于0，也就是说该事件的发生不会导致任何信息量的增加。
举例：
小明平时不爱学习，考试经常不及格，而小王是个勤奋学习的好学生，经常得满分，所以我们可以做如下假设：
事件A：小明考试及格，对应的概率P(xA)=0.1，信息量为I(xA)=−log(0.1)=3.3219
事件B：小王考试及格，对应的概率P(xB)=0.999，信息量为I(xB)=−log(0.999)=0.0014
可以看出，结果非常符合直观：
小明及格的可能性很低(十次考试只有一次及格)，因此如果某次考试及格了（大家都会说：XXX竟然及格了！），必然会引入较大的信息量，对应的I值也较高。而对于小王而言，考试及格是大概率事件，在事件B发生前，大家普遍认为事件B的发生几乎是确定的，因此当某次考试小王及格这个事件发生时并不会引入太多的信息量，相应的I值也非常的低。
什么是熵？
还是通过上边的例子来说明，假设小明的考试结果是一个0-1分布XA，只有两个取值{0：不及格，1：及格}。
在某次考试结果公布前，小明的考试结果有多大的不确定度呢？你肯定会说：十有八九不及格！因为根据先验知识，小明及格的概率仅有0.1,90%的可能都是不及格的。怎么来度量这个不确定度？求期望！不错，我们对所有可能结果带来的额外信息量求取均值（期望），其结果不就能够衡量出小明考试成绩的不确定度了吗。
即：
HA(x)=−[p(xA)log(p(xA))+(1−p(xA))log(1−p(xA))]=0.4690
对应小王的熵：
HB(x)=−[p(xB)log(p(xB))+(1−p(xB))log(1−p(xB))]=0.0114
虽然小明考试结果的不确定性较低，毕竟十次有9次都不及格，但是也比不上小王（1000次考试只有一次才可能不及格，结果相当的确定）
我们再假设一个成绩相对普通的学生小东，他及格的概率是P(xC)=0.5，即及格与否的概率是一样的，对应的熵：
HC(x)=−[p(xC)log(p(xC))+(1−p(xC))log(1−p(xC))]=1
其熵为1，他的不确定性比前边两位同学要高很多，在成绩公布之前，很难准确猜测出他的考试结果。
从上面可以看出，熵其实是信息量的期望值，它是一个随机变量的确定性的度量。熵越大，变量的取值越不确定，反之就越确定。
对于一个随机变量X而言，它的所有可能取值的信息量的期望（E[I(x)]）就称为熵。
X的熵定义为：
如果p(x)是连续型随机变量的pdf，则熵定义为：
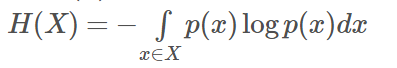
为了保证有效性，这里约定当p(x)→0时,有p(x)logp(x)→0
当X为0-1分布时，熵与概率p的关系如下图：
可以看出，当两种取值的可能性相等时，不确定度最大（此时没有任何先验知识），这个结论可以推广到多种取值的情况。
在图中也可以看出，当p=0或1时，熵为0，即此时X完全确定。
熵的单位随着公式中log运算的底数而变化，当底数为2时，单位为“比特”(bit)，底数为e时，单位为“奈特”。
什么是相对熵？
相对熵(relative entropy)又称为KL散度（Kullback-Leibler divergence），KL距离，是两个随机分布间距离的度量。记为
。它度量当真实分布为p时，假设分布q的无效性。
为了保证连续性，做如下约定： 
显然，当p=q时,两者之间的相对熵
表示在p分布下，使用q进行编码需要的bit数，而H(p)表示对真实分布p所需要的最小编码bit数。
故相对熵的含义为：
表示在真实分布为p的前提下，使用q分布进行编码相对于使用真实分布p进行编码（即最优编码）所多出来的bit数。
什么是交叉熵？
交叉熵容易跟相对熵搞混，二者联系紧密，但又有所区别。
假设有两个分布p，q，则它们在给定样本集上的交叉熵定义如下：
可以看出，交叉熵与上一节定义的相对熵仅相差了H(p)。
当p已知时，可以把H(p)看做一个常数，此时交叉熵与KL距离在行为上是等价的，都反映了分布p，q的相似程度。最小化交叉熵等于最小化KL距离。它们都将在p=q时取得最小值H(p)（p=q时KL距离为0），因此有的工程文献中将最小化KL距离的方法称为Principle of Minimum Cross-Entropy (MCE)或Minxent方法。
特别的，在logistic regression中：
p:真实样本分布，服从参数为p的0-1分布，即X∼B(1,p)X∼B(1,p)
q:待估计的模型，服从参数为q的0-1分布，即X∼B(1,q)X∼B(1,q)
两者的交叉熵为：
对所有训练样本取均值得：
这个结果与通过最大似然估计方法求出来的结果一致。
在机器学习中的交叉熵函数写法：
二分类问题的loss函数（输入数据是softmax或sigmoid函数的输出）：
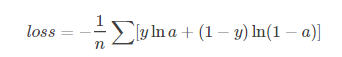
多分类问题使用的loss函数（输入数据是softmax或sigmoid函数的输出）：
如果是在tensorflow中，loss函数往往写成下面这两种形式之一：
loss = tf.reduce_mean(- tf.reduce_sum(y * tf.log(pred), 1))
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=output, labels=Y))
看到上面的二分类和多分类问题使用的loss函数，再跟似然函数比对一下，是不是觉得有点像呢？
事实上，loss函数和对数似然函数形式完全一样。
如果我们从最大似然估计的角度来解读loss函数，那么是这样的：
假如我们的数据集是mnist，这是一个0-9的手写体数字的数据集，如果我们从其中抽出一个图片，总共只有10种可能，即数字0-9。
一般情况下我们每一次训练都是取一个批样本（batch_size）。
我们现在假设batch_size为1，即每次训练只取一个样本。
我们将这个批样本输入神经网络中进行计算，最后得到经过softmax函数或sigmoid函数处理后的输出数据，这个输出数据是我们预测的这batchsize个图片的标签向量，它代表了我们的神经网络预测的这输入的batchsize个样本的每个图片分别是哪一类图片（具体到mnist数据集里，就是图片是数字0-9中的哪一个）。
预测的标签向量的形式为：
[a0,a1,a2,a3,a4,a5,a6,a7,a8,a9]
我们的真实标签也是一个有着同样元素数量的向量，一般写作：
[y0,y1,y2,y3,y4,y5,y6,y7,y8,y9]
且真实标签中除了代表自己是哪个数字的那个下标的元素是1，其他都是0，如[0,0,0,0,0,1,0,0,0,0]代表数字5。
如果我们把一个图片属于数字0-9中的一个看成10个独立事件，其实这个标签向量代表的就是10个独立事件的概率。
而真实标签代表的就是我们抽取的一个样本。这一个样本中必然会发生一个事件，而其他9个事件都不发生。
现在再看看多分类的loss函数：
还记得上面的多分类的似然函数的形式吗？就是这个：
现在回到我们的mnist识别问题，对于loss函数，我们的样本只有1个了，我们现在抽了一个样本是数字7。
设图片是数字0-9的概率分别是x0，x1，x2，x3，x4，x5，x6，x7，x8，x9，那么似然函数为：
对数似然函数为：
这个形式是不是与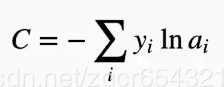
一样呢？很显然是一样的。
为什么多了一个负号？
因为ai总是在0到1之间，而yi值不是0就是1，这就导致每一项要么为0，要么是负数。而tensorflow的优化器是向着loss值降低的方向优化的，并且最终目标是loss值尽可能接近0，所以要求loss函数是一个大于0的值。因此我们加一个负号。
同上面的多分类最大似然估计问题一样，我们一般情况下很难求极值点。
在机器学习中，通过tensorflow使用梯度下降或其他的优化方法，我们可以不断地更新权重参数，最终使得loss函数从一个正值减小到接近0（也就是似然函数从原来的负值逐渐接近0,在这个mnist的例子中显然0是似然函数的极大值）求出一个接近似然函数极大值的点，这就是我们求出的一个接近极大似然估计值的一组ai值。
也就是说，loss函数值越小，求得的ai值代表的概率越有可能是真实概率。
二分类的loss函数也与上面的原理类似，事实上，二分类的loss函数可以用多分类的loss函数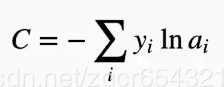
来表达，它们的结果完全一样。
在李航的《统计学习方法》一书中的6.1.3中，推导了二分类的对数似然函数，如下：
如果有兴趣，可以自己详细看看书上的推导过程。
假如batch_size为100（或大于1的其他数），我们的loss函数又是如何处理的呢？
其实看我们在tensorflow中的loss函数变量的定义就知道了：
loss = tf.reduce_mean(- tf.reduce_sum(y * tf.log(pred), 1))
这个loss函数的意思是，yi与对应的ln(ai)相乘后，使用tf.reduce_sum函数将相乘后的这个向量（相乘后的向量形式是shape=(batch_size、10)的张量）按行求和（其实就是求出了每一个样本的loss值）,然后按列求和后求平均值。
也就是说，当输入一个批样本时，我们使用tensorflow优化器更新权重的依据是这一批样本的loss值的平均值。然后通过求loss对各个权重的梯度（链式求导法则），再用梯度更新各个权重。
举例：
假设有一个三分类问题。
第一个样例的正确答案是(1, 0, 0)，经过softmax后的预测答案是(0.5, 0.4, 0.1)
则它和正确答案的交叉熵为： H( (1,0,0) , (0.5,0.4,0.1) ) = - ( 1*log0.5 + 0*log0.4 + 0*log0.1 ) ≈ 0.3
另一个样例经过softmax的预测值是(0.8, 0.1, 0.1)
则他和正确答案的交叉熵是 ： H( (1, 0, 0), (0.8, 0.1, 0.1) ) = - ( 1*log0.8 + 0*log0.1 + 0*log0.1 ) ≈ 0.1
从直观上看容易知道第二个优于第一个，通过交叉熵计算结果也是一致的。所以我们的优化器总是向着loss值减小的方向去优化。