视觉SLAM十四讲学习记录 第四讲

之前第三讲的地址

第四讲 李群与李代数

  在第3讲中，我们介绍了三维世界中刚体运动的描述方式。并且在其中我们重点介绍了旋转的表示。不过在SLAM中，除了表示，我们还要对它们进行估计和优化。因为在SLAM中位姿是未知的，而我们需要解决形如“什么样的相机位姿最符合当前观测数据”这样的问题。一种典型的方式是把它构建成一个优化问题，求解最优的$R,t,$使得误差最小化。
  如前所言，旋转矩阵自身是带有约束的（正交且行列式为1）。它们作为优化变量时，会引入额外的约束，使优化变得困难。通过李群——李代数间的转换关系，我们希望把位姿估计变成无约束的优化问题，简化求解方式。

4.1 李群与李代数基础

  第3讲中，我们介绍了旋转矩阵和变换矩阵的定义。当时，我们说三维旋转矩阵构成了特殊正交群SO(3),而变换矩阵构成了特殊欧氏群SE(3)。它们写起来像这样：
          S O ( 3 ) = { R ∈ R 3 × 3 ∣ R R T = I , d e t ( R ) = 1 } SO(3) = \{R∈\mathbb{R}^{3 × 3}|RR^T = I,det(R) = 1\} SO(3)={ R∈R3×3∣RRT=I,det(R)=1}
          S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } SE(3) = \{T=\begin{bmatrix}R&t\\\\0^T&1\end{bmatrix}∈\mathbb{R}^{4 × 4}|R ∈ SO(3),t ∈ \mathbb{R}^3\} SE(3)={ T=⎣ ⎡​R0T​t1​⎦ ⎤​∈R4×4∣R∈SO(3),t∈R3}
  不过，当时我们并未详细解释群的含义。读者应该可以注意到，旋转矩阵也好，变换矩阵也好，**它们对加法是不封闭的。**换句话说，对任意两个旋转矩阵$R_1,R_2,$按照矩阵加法的定义，和不再是一个旋转矩阵：

         $R_1+R_2\notin SO(3),T_1+T_2\notin SE(3).$

你也可以说两种矩阵并没有良好定义的加法，或者通常矩阵加法对这两个集合不封闭。相对地，它们只有一种较好的运算：乘法。$SO(3)$和$SE(3)$关于乘法是封闭的：

         $R_1{R}_2\in SO(3),T_1{T}_2\in SE(3).$

同时，我们也可以对任何一个旋转或变换矩阵（在乘法的意义上）求逆。我们知道，乘法对应着旋转或变换的复合，两个旋转矩阵相乘表示做了两次旋转。对于这种只有一个（良好的）运算的集合，我们称之为群。

4.1.1 群

  接下来，我们需要介绍一些抽象代数方面的知识。
  群（Group）是一种集合加上一种运算的代数结构。我们把集合记作$A,$运算记作$\cdot ,$那么群可以记作$G=(A,\cdot )。$群要求这个运算满足以下几个条件：

1. 封闭性： $\forall a_1,a_2\in A,a_1\cdot a_2\in A.$
2. 结合律：$\forall a_1,a_2,a_3\in A,(a_1\cdot a_2)\cdot a_3=a_1\cdot (a_2\cdot a_3)$
3. 幺元：$\exists a_0\in A,s.t.\forall a\in A,a_0\cdot a=a\cdot a_0=a.$
4. 逆：$\forall a\in A,\exists a^{-1}\in A,s.t.a\cdot a^{-1}=a_0.$

  读者可以将上述四个性质记作“封结幺逆”。容易验证，旋转矩阵集合和矩阵乘法构成群，同样，变换矩阵和矩阵乘法也构成群（因此才能称它们为旋转矩阵群和变换矩阵群）。其他常见的群包括整数的加法$(\mathbb{Z},+),$去掉0后的有理数的乘法（幺元为1）$(\mathbb{Q}\setminus 0,\cdot )，$等等。矩阵中常见的群有：

• 一般线性群$GL(n)$  指 $n\times n$ 的可逆矩阵，它们对矩阵乘法成群。
• 特殊正交群$SO(n)$  也就是所谓的旋转矩阵群，其中$SO(2)$和$SO(3)$最为常见。
• 特殊欧氏群$SE(n)$  也就是前面提到的$n$维欧氏变换，如$SE(2)$和$SE(3)$。

  群结构保证了在群上的运算具有良好的性质，群论则是研究群的各种结构和性质的理论。对群论感兴趣的读者可以参考任意一本近世代数教材。李群是指具有连续（光滑）性质的群。像整数群$\mathbb{Z}$那样离散的群没有连续性质，所以不是李群。而$SO(n)$和$SE(n)$在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动，所以它们都是李群。由于$SO(3)$和$SE(3)$对于相机姿态估计尤其重要，所以我们主要讨论这两个李群。再从较简单的$SO(3)$开始讨论，引出$SO(3)$上面的李代数$\mathfrak{so}(3)$

4.1.2 李代数的引出

  考虑任意旋转矩阵$R,$我们知道它满足：

         $R{R}^T=I$

现在，我们说，$R$是某个相机的旋转，它会随时间连续地变化，即为时间的函数：$R(t)。$由于它仍是旋转矩阵，有

         $R(t)R(t{)}^T=I$

在等式两边对时间求导，得到

         $\dot{R}(t)R(t{)}^T+R(t)\dot{R}(t{)}^T=0$

整理得

         $\dot{R}(t)R(t{)}^T=-(\dot{R}(t)R(t{)}^T{)}^T$

  可以看出,$\dot{R}(t)R(t{)}^T$是一个反对称矩阵。在之前介绍叉积时，引入了^符号，将一个向量变成了反对称矩阵。同理，对于任意反对称矩阵，我们也能找到唯一与之对应的向量，把这个运算用符号$\stackrel{ˇ}{}$ 表示：

         $a^{\wedge }=A=\left[\begin{array}{ccc}0& -a_3& a_2\\ & & \\ a_3& 0& -a_1\\ & & \\ -a_2& a_1& 0\end{array}\right],A^{\vee }=a$

  于是，由于$\dot{R}(t)R(t{)}^T$是一个反对称矩阵，我们可以找到一个三维向量$\varphi (t)\in {\mathbb{R}}^3$与之对应：

         $\dot{R}(t)R(t{)}^T=\varphi (t{)}^{\wedge }.$

  等式两边右乘$R(t),$由于$R$为正交阵，有

         $\dot{R}(t)=\varphi (t{)}^{\wedge }R(t)=\left[\begin{array}{ccc}0& -{\varphi }_3& {\varphi }_2\\ & & \\ {\varphi }_3& 0& -{\varphi }_1\\ & & \\ -{\varphi }_2& {\varphi }_1& 0\end{array}\right]R(t).$

  可以看到，每对旋转矩阵求一次导数，只需左乘一个${\varphi }^{\wedge }(t)$矩阵即可。考虑$t_0=0$时，设此时旋转矩阵为$R(0)=I。$按照导数定义，可以把$R(t)$在$t=0$附近进行一阶泰勒展开：

         $\begin{array}{rl}R(t)& \approx R(t_0)+\dot{R}(t_0)(t-t_0)\\ & =I+\varphi (t_0{)}^{\wedge }(t).\end{array}$

  我们看到$\varphi$反映了$R$的导数性质，故称它在$SO(3)$原点附近的正切空间（Tangent Space）上。同时在$t_0$附近，设$\varphi$保持为常数$\varphi (t_0)={\varphi }_0。$故有：

         $\dot{R}(t)=\varphi (t_0{)}^{\wedge }R(t)={\varphi }_0^{\wedge }R(t).$

  上式是一个关于$R$的微分方程，而且有初始值$R(0)=I$，解得

         $R(t)=\exp ({\varphi }_0^{\wedge }t).$

  读者可以验证上式对微分方程和初始值均成立。这说明在$t=0$附近，旋转矩阵可以由$\exp ({\varphi }_0^{\wedge }t)$计算出来。我们看到，旋转矩阵$R$与另一个反对称矩阵 ${\varphi }_0^{\wedge }t$通过指数关系发生了联系。但是矩阵的指数是什么呢？这里我们有两个问题需要澄清：

1. 给定某时刻的$R，$我们就能求得一个$\varphi ，$它描述了$R$在局部的导数关系。与$R$对应的$\varphi$有什么含义呢？我们说，$\varphi$正是对应到$SO(3)$上的李代数$\mathfrak{so}(3);$
2. 其次，给定某个向量$\varphi$时，矩阵指数$\exp ({\varphi }^{\wedge })$如何计算？反之，给定$R$时，能否有相反的运算来计算$\varphi ?$事实上，这正是李群与李代数间的指数/对数映射。

  下面，我们会解决这两个问题。

4.1.3 李代数的定义

  每个李群都有与之对应的李代数。李代数描述了李群的局部性质，准确地说，是单位元附近的正切空间。一般的李代数的定义如下：
  李代数由一个集合$\mathbb{V}、$一个数域$\mathbb{F}$和一个二元运算$[,]$组成。如果它们满足以下几条性质，则称$(\mathbb{V},\mathbb{F},[,])$为一个李代数，记作$\mathfrak{g}。$

1. 封闭性 $\forall X,Y\in \mathbb{V},[X,Y]\in \mathbb{V}.$
2. 双线性 $\forall X,Y,Z\in \mathbb{V},a,b\in \mathbb{F},$有
            $[aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[Z,X]+b[Z,Y].$
3. 自反性 $\forall X\in \mathbb{V},[X,X]=0.$
4. 雅可比等价 $\forall X,Y,Z\in \mathbb{V},[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0$

其中二元运算被称为李括号。从表面上看，李代数所需要的性质还是挺多的。相比于群中的较为简单的二元运算，李括号表达了两个元素的差异。它不要求结合律，而要求元素和自己做李括号之后为零的性质。作为例子，三维向量${\mathbb{R}}^3$上定义的叉积×是一种李括号，因此$\mathfrak{g}=({\mathbb{R}}^3,\mathbb{R},\times )$构成了一个李代数。

4.1.4 李代数$\mathfrak{so}(3)$

  之前提到的$\varphi ，$事实上是一种李代数。$SO(3)$对应的的是定义在${\mathbb{R}}^3$上的向量，我们记作$\varphi$。根据前面的推导，每个$\varphi$都可以生成一个反对称矩阵：

         $\Phi ={\varphi }^{\wedge }=\left[\begin{array}{ccc}0& -{\varphi }_3& {\varphi }_2\\ & & \\ {\varphi }_3& 0& -{\varphi }_1\\ & & \\ -{\varphi }_2& {\varphi }_1& 0\end{array}\right]\in {\mathbb{R}}^{3\times 3}.$
  在此定义下，两个向量${\varphi }_1,{\varphi }_2$的李括号为

         $[{\varphi }_1,{\varphi }_2]=({\Phi }_1{\Phi }_2-{\Phi }_2{\Phi }_1{)}^{\vee }.$

  读者可以验证该定义下的李括号是否满足上面的四条性质。由于向量$\varphi$与反对称矩阵是一一对应的，在不引起歧义的情况下，就说$\mathfrak{so}(3)$的元素是三维向量或者三维反对称矩阵，不加区别：

          s o ( 3 ) = { ϕ ∈ R 3 , Φ = ϕ ∧ ∈ R 3 × 3 } . \mathfrak{so}(3) = \{\phi \in \mathbb{R}^3,\Phi = \phi^{\land} \in \mathbb{R}^{3 × 3}\}. so(3)={ ϕ∈R3,Φ=ϕ∧∈R3×3}.

有些书里也会用$\hat{\varphi }$这样的符号表示反对称，但意义是一样的。至此，我们已清楚了$\mathfrak{so}(3)$的内容。它们是一个由三维向量组成的，每个向量对应一个反对称矩阵，可以用于表达旋转矩阵的导数。它与$SO(3)$的关系由指数映射给定：

         $R=\exp ({\varphi }^{\wedge }).$

指数映射会在稍后介绍。由于已经介绍了$\mathfrak{so}(3),$我们顺带再来看看$SE(3)$对应的李代数。

4.1.5 李代数$\mathfrak{se}(3)$

  对于$SE(3)$，也有对应的李代数$\mathfrak{se}(3)。$为节省篇幅，这里就不介绍如何引出$\mathfrak{se}(3)$了。与$\mathfrak{so}(3)$相似，$\mathfrak{se}(3)$位于${\mathbb{R}}^6$空间中：

         $\mathfrak{se}(3)=\left\{\xi =\left[\begin{array}{c}\rho \\ \\ \varphi \end{array}\right]\in {\mathbb{R}}^6,\rho \in {\mathbb{R}}^3,\varphi \in \mathfrak{so}(3),{\xi }^{\wedge }=\left[\begin{array}{cc}{\varphi }^{\wedge }& \rho \\ & \\ 0^T& 0\end{array}\right]\in {\mathbb{R}}^{4\times 4}\right\}.$

我们把每个$\mathfrak{se}(3)$元素记作$\xi ，$它是一个六维向量。前三维为平移，记作$\rho ；$后三维为旋转，记作$\varphi ，$实质上是$\mathfrak{so}(3)$元素。同时，我们拓展了$\stackrel{ˆ}{}$ 符号的含义。在$\mathfrak{se}(3)$中，同样使用$\stackrel{ˆ}{}$ 符号，将一个六维向量转换成四维矩阵，但这里不再表示反对称：

         ${\xi }^{\wedge }=\left[\begin{array}{cc}{\varphi }^{\wedge }& \rho \\ & \\ 0^T& 0\end{array}\right]\in {\mathbb{R}}^{4\times 4}.$

  我们仍使用$\stackrel{ˆ}{}$ 和$\stackrel{ˇ}{}$ 符号指代“从向量到矩阵”和“从矩阵到向量”的关系，以保持和$\mathfrak{so}(3)$上的一致性。它们依旧是一一对应的。读者可以简单地把$\mathfrak{se}(3)$理解成“由一个平移加上一个$\mathfrak{so}(3)$元素构成的向量”（尽管这里的$\rho$还不直接是平移）。同样，李代数$\mathfrak{se}(3)$也有类似于$\mathfrak{so}(3)$的李括号：

         $[{\xi }_1,{\xi }_2]=({\xi }_1^{\wedge }{\xi }_2^{\wedge }-{\xi }_2^{\wedge }{\xi }_1^{\wedge }{)}^{\vee }.$

  读者可以验证它是否满足李代数的定义。至此，我们已经见过两种重要的李代数$\mathfrak{so}(3)$和$\mathfrak{se}(3)$了。

4.2 指数与对数映射

4.2.1 $SO(3)$上的指数映射

  现在来考虑第二个问题：如何计算$\exp ({\varphi }^{\wedge })?$显然它是一个矩阵的指数，在李群和李代数中，称为指数映射（Exponential Map）。同样，我们会先讨论$\mathfrak{so}(3)$的指数映射，再讨论$\mathfrak{se}(3)$的情形。
  任意矩阵的指数映射可以写成一个泰勒展开，但是只有在收敛的情况下才会有结果，其结果仍是一个矩阵：

         $\exp (A)=\sum _{n=0}^{\infty }\frac{1}{n!}{A}^n.$

  同样地，对$\mathfrak{so}(3)$中的任意元素$\varphi ，$我们也可按此方式定义它的指数映射：

         $\exp ({\varphi }^{\wedge })=\sum _{n=0}^{\infty }\frac{1}{n!}({\varphi }^{\wedge }{)}^n.$

但这个定义没法直接计算，因为我们不想计算矩阵的无穷次幂。下面我们推导一种计算指数映射的简便方法。由于$\varphi$是三维向量，我们可以定义它的模长和方向，分别记作$\theta$和$a，$于是有$\varphi =\theta a。$这里$a$是一个长度为1的方向向量，即$\Vert a\Vert =1。$首先，对于$a^{\wedge },$有以下两条性质：

         $a^{\wedge }{a}^{\wedge }=\left[\begin{array}{ccc}-a_2^2-a_3^2& a_1{a}_2& a_1{a}_3\\ & & \\ a_1{a}_2& -a_1^2-a_3^2& a_2{a}_3\\ & & \\ a_1{a}_3& a_2{a}_3& -a_1^2-a_2^2\end{array}\right]=a{a}^T-I,$

  以及

         $a^{\wedge }{a}^{\wedge }{a}^{\wedge }=a^{\wedge }(a{a}^T-I)=-a^{\wedge }.$

这两个式子提供了处理$a^{\wedge }$高阶项的方法。我们可以把指数映射写成

         $\begin{array}{rl}\exp ({\varphi }^{\wedge })=\exp (\theta a^{\wedge })& =\sum _{n=0}^{\infty }\frac{1}{n!}(\theta a^{\wedge }{)}^n\\ & =I+\theta a^{\wedge }+\frac{1}{2!}{\theta }^2{a}^{\wedge }{a}^{\wedge }+\frac{1}{3!}{\theta }^3{a}^{\wedge }{a}^{\wedge }{a}^{\wedge }+\frac{1}{4!}{\theta }^4(a^{\wedge }{)}^4+\cdot \cdot \cdot \\ & =a{a}^T-a^{\wedge }{a}^{\wedge }+\theta a^{\wedge }+\frac{1}{2!}{\theta }^2{a}^{\wedge }{a}^{\wedge }-\frac{1}{3!}{\theta }^3{a}^{\wedge }-\frac{1}{4!}{\theta }^4(a^{\wedge }{)}^2+\cdot \cdot \cdot \\ & =a{a}^T+\begin{array}{c}\underbrace{(\theta -\frac{1}{3!}{\theta }^3+\frac{1}{5!}{\theta }^5-\cdot \cdot \cdot )}\\ \sin \theta \end{array}{a}^{\wedge }-\begin{array}{c}\underbrace{(1-\frac{1}{2!}{\theta }^2+\frac{1}{4!}{\theta }^4-\cdot \cdot \cdot )}\\ \cos \theta \end{array}{a}^{\wedge }{a}^{\wedge }\\ & =a^{\wedge }{a}^{\wedge }+I+\sin \theta a^{\wedge }-\cos \theta a^{\wedge }{a}^{\wedge }\\ & =(1-\cos \theta )a^{\wedge }{a}^{\wedge }+I+\sin \theta a^{\wedge }\\ & =\cos \theta I+(1-\cos \theta )a{a}^T+\sin \theta a^{\wedge }\end{array}$

  最后，得到一个似曾相识的式子：

         $\exp (\theta a^{\wedge })=\cos \theta I+(1-\cos \theta )a{a}^T+\sin \theta a^{\wedge }.$

  回想第3讲的内容，它和罗德里格斯公式如出一辙。这表明，$\mathfrak{so}(3)$实际上就是由所谓的旋转向量组成的空间，而指数映射即罗德里格斯公式。通过它们，我们把$\mathfrak{so}(3)$中任意一个向量对应到了一个位于$SO(3)$中的旋转矩阵。反之，如果定义对数映射，也能把$SO(3)$中的元素对应到$\mathfrak{so}(3)$中：

         $\varphi =\ln (R{)}^{\vee }={\left(\sum _{n=0}^{\infty }\frac{(-1{)}^n}{n+1}(R-I{)}^{n+1}\right)}^{\vee }.$

和指数映射一样，我们没必要直接用泰勒展开计算对数映射。在第3讲中，我们介绍过如何根据旋转矩阵计算对应的李代数，利用迹的性质分别求解转角和转轴，采用这种方式更省事。
  现在，我们介绍了指数映射的计算方法。那么，指数映射有何性质呢？是否对于任意的$R$都能找到一个唯一的$\varphi ?$很遗憾，指数映射只是一个满射，并不是单射（有关满射、单射、双射参考图灵的猫i的文章）。这意味着每个$SO(3)$中的元素，都可以找到一个$\mathfrak{so}(3)$元素与之对应；但是可能存在多个$\mathfrak{so}(3)$中的元素，对应到同一个$SO(3)$。至少对于旋转角$\theta$，我们知道多转$360°$和没有转是一样的——它既有周期性。但是，如果我们把旋转角度固定在$\pm \pi$之间，那么李群和李代数元素是一一对应的。
  $SO(3)$与$\mathfrak{so}(3)$的结论似乎在我们的意料之中。它和我们前面讲的旋转向量与旋转矩阵很相似，而指数映射即罗德里格斯公式。旋转矩阵的导数可以由旋转向量指定，指导着如何在旋转矩阵中进行微积分运算。

4.2.2 $SE(3)$上的指数映射

  下面介绍$\mathfrak{se}(3)$上的指数映射。如上，形式如下：

         $\begin{array}{rl}\exp ({\xi }^{\wedge })& =\left[\begin{array}{cc}\sum _{n=0}^{\infty }\frac{1}{n!}({\varphi }^{\wedge }{)}^n& \sum _{n=0}^{\infty }\frac{1}{(n+1)!}({\varphi }^{\wedge }{)}^n\rho \\ & \\ 0^T& 1\end{array}\right]\\ & \\ & \stackrel{\Delta }{=}\left[\begin{array}{cc}R& Jp\\ & \\ 0^T& 1\end{array}\right]=T\end{array}$

  只要有一点耐心，可以照着$\mathfrak{so}(3)$上的做法推导，把$\exp$进行泰勒展开推导此事。令$\varphi =\theta a,$其中$a$为单位向量，则

         $\begin{array}{rl}\sum _{n=0}^{\infty }\frac{1}{(n+1)!}({\varphi }^{\wedge }{)}^n& =I+\frac{1}{2!}\theta a^{\wedge }+\frac{1}{3!}{\theta }^2(a^{\wedge }{)}^2+\frac{1}{4!}{\theta }^3(a^{\wedge }{)}^3+\frac{1}{5!}{\theta }^4(a^{\wedge }{)}^4\cdot \cdot \cdot \\ & =\frac{1}{\theta }\begin{array}{c}(\frac{1}{2!}{\theta }^2-\frac{1}{4!}{\theta }^4+\cdot \cdot \cdot )\end{array}(a^{\wedge })+\frac{1}{\theta }\begin{array}{c}(\frac{1}{3!}{\theta }^3-\frac{1}{5!}{\theta }^5+\cdot \cdot \cdot )\end{array}(a^{\wedge }{)}^2+I\\ & =\frac{1}{\theta }(1-\cos \theta )(a^{\wedge })+\frac{\theta -\sin \theta }{\theta }(a{a}^T-I)+I\\ & =\frac{\sin \theta }{\theta }I+(1-\frac{\sin \theta }{\theta })a{a}^T+\frac{1-\cos \theta }{\theta }{a}^{\wedge }\stackrel{def}{=}J.\end{array}$

  从结果上看，$\xi$的指数映射左上角的$R$是我们熟知的$SO(3)$中的元素，与$\mathfrak{se}(3)$中的旋转部分$\varphi$对应。而右上角的$J$由上面的推导给出：

         $J=\frac{\sin \theta }{\theta }I+(1-\frac{\sin \theta }{\theta })a{a}^T+\frac{1-\cos \theta }{\theta }{a}^{\wedge }.$

  该式与罗德里格斯公式有些相似，但不完全一样。我们看到，平移部分经过指数映射之后，发生了一次以$J$为系数矩阵的线性变换。
  同样地，虽然我们也可以类比推得对数映射，不过根据变换矩阵$T$求$\mathfrak{so}(3)$上的对应向量有更省事的方式：从左上角的$R$计算旋转向量，而右上角的$t$满足：

         $t=J\rho .$

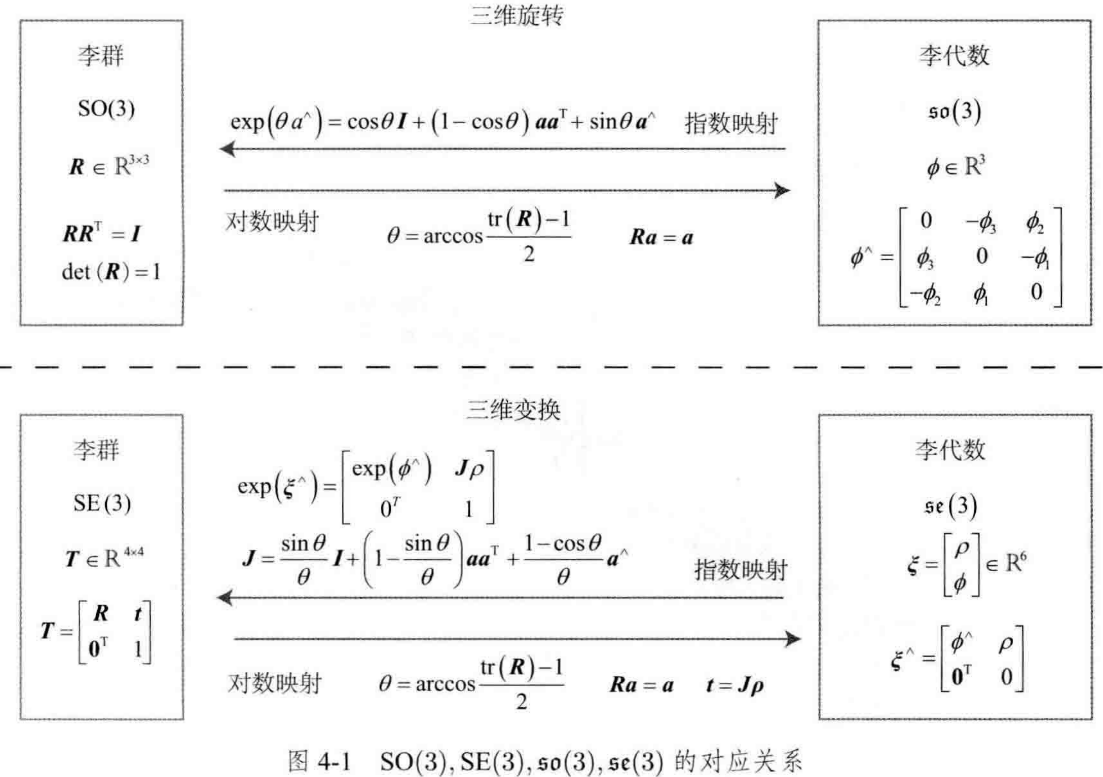
  由于$J$可以由$\varphi$得到，所以这里的$\rho$也可以由此线性方程解得。现在，我们已经弄清了李群、李代数的定义与相互的转换关系，如下图所示：

4.3 李代数求导与扰动模型

4.2.1 BCH公式与近似形式

  使用李代数的一大动机是进行优化，而在优化过程中导数是非常必要的信息。下面来考虑一个问题。虽然我们已经清楚了$SO(3)$和$SE(3)$上的李群与李代数关系，但是，当在$SO(3)$中完成两个矩阵乘法时，李代数中$\mathfrak{so}(3)$上发生了什么改变呢？反过来说，当$\mathfrak{so}(3)$上做两个李代数的加法时，$SO(3)$是否对应着两个矩阵的乘积？如果成立，相当于：

         $\exp ({\varphi }_1^{\wedge })\exp ({\varphi }_2^{\wedge })=\exp (({\varphi }_1+{\varphi }_2{)}^{\wedge })?$

  如果${\varphi }_1,{\varphi }_2$为标量，那么显然该式成立；但此时我们计算的是矩阵的指数函数，而非标量的指数。换言之，我们在研究下式是否成立：

         $\ln (\exp (A)\exp (B))=A+B？$

  很遗憾，该式在矩阵时并不成立。两个李代数指数映射乘积的完整形式，由Baker-Campbell-Hausdorff公式(BCH公式)给出。由于其完整形式较复杂，我们只给出其展开式的前几项：

         $\ln (exp(A)\exp (B))=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+\cdot \cdot \cdot$

  其中$[]$为李括号。BCH公式告诉我们，当处理两个矩阵指数之积时，它们会产生一些由李括号组成的余项。特别地，考虑$SO(3)$上的李代数$\ln (exp({\varphi }_1^{\wedge })\exp ({\varphi }_2^{\wedge }){)}^{\vee },$当${\varphi }_1$或${\varphi }_2$为小量时，小量二次以上的项都可以被忽略。此时，BCH拥有线性近似表达：

         $\ln (exp({\varphi }_1^{\wedge })\exp ({\varphi }_2^{\wedge }){)}^{\vee }\approx \{\begin{array}{ll}{J}_l({\varphi }_2{)}^{-1}{\varphi }_1+{\varphi }_2& 当{\varphi }_1为小量,\\ J_r({\varphi }_1{)}^{-1}{\varphi }_2+{\varphi }_1& 当{\varphi }_2为小量,\end{array}$

  以第一个近似为例。该式告诉我们，当对一个旋转矩阵$R_2$(李代数为${\varphi }_2$)左乘一个微小旋转矩阵$R_1$(李代数为${\varphi }_1$)时，可以近似地看作，在原有的李代数${\varphi }_2$上加上了一项$J_l({\varphi }_2{)}^{-1}{\varphi }_1。$同理，第二个近似描述了右乘一个微小位移的情况。于是李代数在BCH近似下，分成了左乘近似和右乘近似两种，在使用时我们须注意使用的是左乘模型还是右乘模型。
  本书以左乘为例。左乘BCH近似雅可比$J_l$事实上就是式(4.27)的内容：

         $J_l=J=\frac{\sin \theta }{\theta }I+(1-\frac{\sin \theta }{\theta })a{a}^T+\frac{1-\cos \theta }{\theta }{a}^{\wedge }.$

  它的逆为

         $J_l^{-1}=\frac{\theta }{2}\cot \frac{\theta }{2}I+(1-\frac{\theta }{2}\cot \frac{\theta }{2})a{a}^T-\frac{\theta }{2}{a}^{\wedge }.$

而右乘雅可比仅需要对自变量取负号即可：

         $J_r(\varphi )=J_l(-\varphi ).$

  这样，我们就可以谈论李群乘法与李代数加法的关系了。
  为了方便读者理解，我们重新叙述BCH近似的意义。假定对某个旋转$R,$ 对应的李代数为$\varphi 。$我们给它左乘一个微小旋转，记作$\Delta R,$对应的李代数为$\Delta \varphi 。$那么，在李群上，得到的结果就是$\Delta R\cdot R,$ 而在李代数上，根据BCH近似，为$J_l^{-1}(\varphi )\Delta \varphi +\varphi 。$合并起来，可以简单地写成：

         $\exp (\Delta {\varphi }^{\wedge })\exp ({\varphi }^{\wedge })=\exp ((\varphi +J_l^{-1}(\varphi )\Delta \varphi {)}^{\wedge }).$

  反之，如果我们在李代数上进行加法，让一个$\varphi$加上$\Delta \varphi ，$让一个$\varphi$加上$\Delta \varphi ，$那么可以近似为李群上带左右雅可比的乘法：

         $\exp ((\varphi +\Delta \varphi {)}^{\wedge }))=\exp ((J_l\Delta \varphi {)}^{\wedge })\exp ({\varphi }^{\wedge })=\exp ({\varphi }^{\wedge })\exp ((J_r\Delta \varphi {)}^{\wedge }).$

  这就为之后李代数上做微积分提供了理论基础。同样地，对于$SE(3),$也有类似的BCH近似：

         $\exp (\Delta {\xi }^{\wedge })\exp ({\xi }^{\wedge })\approx \exp (({\mathcal{J}}_l^{-1}\Delta \xi +\xi {)}^{\wedge }),$
         $\exp ({\xi }^{\wedge })\exp (\Delta {\xi }^{\wedge })\approx \exp (({\mathcal{J}}_r^{-1}\Delta \xi +\xi {)}^{\wedge }).$

  这里$\mathcal{J_l}形式比较复杂，它是一个 $6\times 6$的矩阵。由于我们在计算中没有用到该雅可比，故这里略去它的实际形式。

4.3.2 SO(3)上的李代数求导

  下面来讨论一个带有李代数的函数，以及关于该李代数求导的问题。该问题有很强的实际背景。在SLAM中，我们要估计一个相机的位置和姿态，该位姿是由$SO(3)$上的旋转矩阵或$SE(3)$上的变换矩阵描述的。不妨设某个时刻小萝卜的位姿为$T。$它观察到了一个世界坐标位于$p$的点，产生了一个观测数据$z。$那么，由坐标变换关系知：

         $z=Tp+w.$

其中$w$为随机噪声。由于它的存在，$z$往往不可能精确地满足$z=Tp$的关系。所以，我们通常会计算理想的观测与实际数据的我误差：

         $e=z-Tp.$

  假设一共有$N$个这样的路标点和观测，于是就有$N$个上式。那么，对小萝卜进行位姿估计，相当于寻找一个最优的$T，$使得整体误差最小化：

         $\underset{T}{\min }J(T)=\sum _{i=1}^N\Vert z_i-T{p}_i{\Vert }_2^2.$

  求解此问题，需要计算目标函数$J$关于变换矩阵$T$的导数。我们把具体的算法留到后面再讲。这里的重点是，**我们经常会构建与位姿有关的函数，然后讨论该函数关于位姿的导数，以调整当前的估计值。**然而，$SO(3),$$SE(3)$上并没有良好定义的加法，它们只是群。如果我们把$T$当成一个普通矩阵来处理优化，就必须对它加以约束。而从李代数角度来说，由于李代数由向量组成，具有良好的加法运算，因此，使用李代数解决求导问题的思路分为两种：

1. 用李代数表示姿态，然后根据李代数加法对李代数求导。
2. 对李群左乘或右乘微小扰动，然后对该扰动求导，称为左扰动和右扰动模型。

  第一种方式对应到李代数的求导模型，而第二种方式则对应到扰动模型。下面讨论下这两种思路的异同。

4.3.3 李代数求导

  首先，考虑$SO(3)$上的情况。假设我们对一个空间点$p$进行了旋转，得到了$Rp$。现在，要计算旋转之后点的坐标相对于旋转的导数，我们非正式地记为

                  $\frac{\partial (Rp)}{\partial (R)}$

由于$SO(3)$没有加法，所以该导数无法按照导数的定义进行计算。设$R$对应的李代数为$\varphi ，$我们转而计算：

                  $\frac{\partial (\exp ({\varphi }^{\wedge })p)}{\partial \varphi }.$

  按照导数的定义，有

         $\begin{array}{rl}\frac{\partial (\exp ({\varphi }^{\wedge })p)}{\partial \varphi }& =\underset{\delta \varphi \to 0}{\lim }\frac{\exp ((\varphi +\delta \varphi {)}^{\wedge })p-\exp ({\varphi }^{\wedge })p}{\delta \varphi }\\ & \\ & =\underset{\delta \varphi \to 0}{\lim }\frac{\exp ((J_l\delta \varphi {)}^{\wedge })\exp ({\varphi }^{\wedge })p-\exp ({\varphi }^{\wedge })p}{\delta \varphi }\\ & \\ & =\underset{\delta \varphi \to 0}{\lim }\frac{(I+(J_l\delta \varphi {)}^{\wedge })\exp ({\varphi }^{\wedge })p-\exp ({\varphi }^{\wedge })p}{\delta \varphi }\\ & \\ & =\underset{\delta \varphi \to 0}{\lim }\frac{(J_l\delta \varphi {)}^{\wedge }\exp ({\varphi }^{\wedge })p}{\delta \varphi }\\ & \\ & =\underset{\delta \varphi \to 0}{\lim }\frac{-(\exp ({\varphi }^{\wedge })p{)}^{\wedge }{J}_l\delta \varphi }{\delta \varphi }=-(Rp{)}^{\wedge }{J}_l\end{array}$

  第2行的近似为BCH线性近似，第3行为泰勒展开舍去高阶项后的近似（由于取了极限，可以写等号），第4行至第5行将反对称符号看作叉积，交换之后变号。于是，我们推导出了旋转后的点相对于李代数的导数：

         $\frac{\partial (Rp)}{\partial \varphi }=(-Rp{)}^{\wedge }{J}_l.$

  不过，由于这里仍然含有形式比较复杂的$J_l,$我们不太希望计算它。而下面介绍的扰动模型则提供了更为简单的导数计算方式。

4.3.4 扰动模型（左乘）

  另一种求导方式是对$R$进行一次扰动$\Delta R$，看结果相对于扰动的变化率。这个扰动可以乘在左边也可以乘在右边，最后结果会有一点儿微小的差异，我们以左扰动为例。设左扰动$\Delta R$对应的李代数$\phi 。$然后，对$\phi$求导，即

         $\frac{\partial (Rp)}{\partial \phi }=\underset{\phi \to 0}{\lim }\frac{\exp ({\phi }^{\wedge })\exp ({\varphi }^{\wedge })p-\exp ({\varphi }^{\wedge })p}{\phi }.$

  该式的求导比上面更简单：

         $\begin{array}{rl}\frac{\partial (Rp)}{\partial \phi }& =\underset{\phi \to 0}{\lim }\frac{\exp ({\phi }^{\wedge })\exp ({\varphi }^{\wedge })p-\exp ({\varphi }^{\wedge })p}{\phi }\\ & \\ & =\underset{\phi \to 0}{\lim }\frac{(I+{\phi }^{\wedge })\exp ({\varphi }^{\wedge })p-\exp ({\varphi }^{\wedge })p}{\phi }\\ & \\ & =\underset{\phi \to 0}{\lim }\frac{{\phi }^{\wedge }Rp}{\phi }=\underset{\phi \to 0}{\lim }\frac{-(Rp{)}^{\wedge }\phi }{\phi }=-(Rp{)}^{\wedge }.\end{array}$

  可见，相比于直接对李代数求导，省去了一个雅可比$J_l$的计算。这使得扰动模型更为实用。请读者务必理解这里的求导运算，这在位姿估计中具有重要的意义。

4.3.5 SE(3)上的李代数求导

  最后，我们给出$SE(3)$上的扰动模型，而直接李代数上的求导就不再介绍了。假设某空间点$p$经过一次变换$T$(对应李代数为$\xi$)，得到$Tp$。现在，给$T$左乘一个扰动$\Delta T=\exp (\delta {\xi }^{\wedge }),$我们设扰动项的李代数为$\delta \xi =[\delta \rho ,\delta \varphi {]}^T,$那么：

         $\begin{array}{rl}\frac{\partial (Tp)}{\partial \delta \xi }& =\underset{\delta \xi \to 0}{\lim }\frac{\exp (\delta {\xi }^{\wedge })\exp ({\xi }^{\wedge })p-\exp ({\xi }^{\wedge })p}{\delta \xi }\\ & \\ & =\underset{\delta \xi \to 0}{\lim }\frac{(I+\delta {\xi }^{\wedge })\exp ({\xi }^{\wedge })p-\exp ({\xi }^{\wedge })p}{\delta \xi }\\ & \\ & =\underset{\delta \xi \to 0}{\lim }\frac{\delta {\xi }^{\wedge }\exp ({\xi }^{\wedge })p}{\delta \xi }\\ & \\ & =\underset{\phi \to 0}{\lim }\frac{\left[\begin{array}{cc}\delta {\varphi }^{\wedge }& \delta \rho \\ & \\ 0^T& 0\end{array}\right]\left[\begin{array}{c}Rp+t\\ \\ 1\end{array}\right]}{\delta \xi }\\ & \\ & =\underset{\phi \to 0}{\lim }\frac{\left[\begin{array}{c}\delta {\varphi }^{\wedge }(Rp+t)+\delta \rho \\ \\ 0^T\end{array}\right]}{[\delta \rho ,\delta \varphi {]}^T}=\left[\begin{array}{cc}I& -(Rp+t{)}^{\wedge }\\ & \\ 0^T& 0^T\end{array}\right]\stackrel{def}{=}(Tp{)}^{⨀}.\end{array}$

  我们把最后的结果定义成一个算符${}^{⨀}$，它把一个齐次坐标的空间点变换成一个$4\times 6$的矩阵。此式稍微需要解释的是矩阵求导方面的顺序，假设$a,b,x,y$都是列向量，那么在我们的写法下，有如下的规则：

         $\frac{d\left[\begin{array}{c}\\ \\ a\\ \\ b\\ \end{array}\right]}{d\left[\begin{array}{c}\\ \\ x\\ \\ y\\ \end{array}\right]}=\left(\frac{d[a,b{]}^T}{d\left[\begin{array}{c}\\ \\ x\\ \\ y\\ \end{array}\right]}\right)={\left[\begin{array}{cc}\frac{da}{dx}& \frac{db}{dx}\\ & \\ \frac{da}{dy}& \frac{db}{dy}\end{array}\right]}^T=\left[\begin{array}{cc}\frac{da}{dx}& \frac{da}{dy}\\ & \\ \frac{db}{dx}& \frac{db}{dy}\end{array}\right]$

  至此，我们已经介绍了李群与李代数上的微分运算。之后的章节中，我们将应用这些知识解决实际问题。关于李群与李代数的某些重要数学性质，我们作为习题留给读者。

4.4 实践：Sophus

4.4.1 Sophus的基本使用方法

  我们已经介绍了李代数的入门知识，现在是通过实践演练并巩固所学知识的时候了。我们来讨论如何在程序中操作李代数。在第3讲中，我们看到Eigen提供了几何模块，但没有提供李代数的支持。一个较好的李代数库是Strasdat维护的Sophus库。Sophus库支持本章主要讨论的$SO(3)$和$SE(3)，$此外，还含有二维运动$SO(2),SE(2)$及相似变换Sim(3)的内容。它是直接在Eigen基础上开发的，我们不需要安装额外的依赖库。Sophus早期版本只提供了双精度的李群/李代数类。后续版本改成了模板类。模板类的Sophus中可以使用不同精度的李群/李代数，但同时增加了增加了使用难度。在本书中，我们使用带模板的Sophus库。
  具体见slambook/ch4/useSophus.cpp来演示Sophus库中的$SO(3)$和$SE(3)$运算：
  运行结果如下：

  上述程序演示了两个部分的内容。前半部分介绍$SO(3)$上的操作，后半部分则为$SE(3)。$我们演示了如何构造$SO(3),SE(3)$对象，对它们进行指数、对数映射，以及当知道更新量后，如何对李群元素进行更新。当理解了本讲内容，那么这个程序对你来说应该没有什么难度。为了编译，需要在CMakeLists.txt里添加以下几行代码：

find_package( Sophus REQUIRED)
include_directories( ${
    
    Sophus_INCLUDE_DIRS})

add_executable( useSophus useSophus.cpp)

  find_package命令是cmake提供的寻找某个库的头文件与库文件的指令。如果cmake能够找到它，就会提供头文件和库文件所在的目录的变量。在Sophus这个例子中，就是Sophus_INCLUDE_DIRS。基于模板的Sophus库和Eigen一样，是仅含头文件而没有源文件的。根据它们，我们就能将Sophus库引入自己的cmake工程。

4.4.2 例子：评估轨迹的误差

  在实际工程中，我们经常需要评估一个算法的估计轨迹与真实轨迹的差异来评价算法的精度。真实轨迹往往通过某些更高精度的系统获得，而估计轨迹则是由待评价的算法计算得到的。第3讲我们演示了如何显示存储在文件中的某条轨迹，本节我们考虑如何计算两条轨迹的误差。考虑一条估计轨迹$T_{esti,i}$和真实轨迹$T_{gt,i},$其中$i=1,\cdot \cdot \cdot ，N，$那么我们可以定义一些误差指标来描述它们之间的差别。
  误差指标可以有很多种，常见的有绝对轨迹误差（Absolute Trajectory Error， ATE）， 形如：

         $AT{E}_{all}=\sqrt{\frac{1}{N}\sum _{i=1}^N\Vert \log (T_{gt,i}^{-1}{T}_{esti,i}{)}^{\vee }{\Vert }_2^2},$

这实际上是每个位姿李代数的均方根误差（Root-Mean-Squared Error, RMSE）。 这种误差可以刻画两条轨迹的旋转和平移误差。同时，也有的文献仅考虑平移误差，从而可以定义绝对平移误差（Avergae Translational Error）：

         $AT{E}_{trans}=\sqrt{\frac{1}{N}\sum _{i=1}^N\Vert trans(T_{gt,i}^{-1}{T}_{esti,i}){\Vert }_2^2},$

其中trans表示取括号内部变量的平移部分。因为从整条轨迹上看，旋转出现误差后，随后的轨迹在平移上也会出现误差，所以两种指标在实际中都适用。
  除此之外，也可以定义相对的误差。例如，考虑$i$时刻到$i+\Delta t$时刻的运动，那么相对位姿误差可定义为：

         $RP{E}_{all}=\sqrt{\frac{1}{N-\Delta t}\sum _{i=1}^{N-\Delta t}\Vert \log ((T_{gt,i}^{-1}{T}_{gt,i+\Delta t}{)}^{-1}(T_{esti,i}^{-1}{T}_{esti,i+\Delta t}){)}^{\vee }{\Vert }_2^2},$

同样地，也可只取平移部分：

         $RP{E}_{trans}=\sqrt{\frac{1}{N-\Delta t}\sum _{i=1}^{N-\Delta t}\Vert trans((T_{gt,i}^{-1}{T}_{gt,i+\Delta t}{)}^{-1}(T_{esti,i}^{-1}{T}_{esti,i+\Delta t})){\Vert }_2^2},$

  利用Sophus库，很容易实现这部分计算。下面哦们演示绝对轨迹误差的计算。在这个例子中，我们有groundtruth.txt和estimated.txt两条轨迹，下面的代码将读取这两条轨迹，计算误差，然后显示到3D窗口中。为简洁起见，省略了画轨迹部分的代码。在第3讲中我们已经做过类似的工作。
  代码见slambook/ch4/example/trajectoryError.cpp
  使代码运行成功的过程也是异常的曲折，分为三个步骤：

1. 首先报错缺少fmt这个库，是因为新版Sophus不仅需要Pangolin，还需要安装fmt，那便安装即可。
2. 安装完后运行，他还会报错，fmt/core.h:1711:3: error: static assertion failed: Cannot format an argument.百度后说是版本的问题，都推荐使用fmt 8.1.1，好的，下一个该版本的fmt 8.1.1，无需删除前一个版本，直接重复之前的步骤
3. 安装完后，记得在CMakeLists.txt中加入下面两句，让cmake包含这个库，这样便可以使程序运行起来

find_package(FMT REQUIRED) 
target_link_libraries(trajectoryError fmt::fmt)

4. 然后会发现文件地址错了，无法找到两个txt文件的目录。那便需要修改文件的目录
   
   费了我快一个小时才将这个代码跑出来呢~!!
   结果如下：
   
     该程序输出的结果为2.20728。当然也可以去掉旋转部分，仅计算平移部分的误差。就这个例子来说，我们事实上已经帮助读者做了一些预处理任务，包括轨迹的时间对齐、外参预估，这些内容现在还没有提到，以后的学习中会说到。

4.5 * 相似变换群与李代数

  最后，我们要提一下在单目视觉中使用的相似群$Sim(3)$，以及对应的李代数$\mathfrak{sim}(3)。$
  我们已经介绍过单目的尺度不确定性。如果在单目SLAM中使用$SE(3)$表示位姿，那么由于尺度不确定性与尺度漂移，整个SLAM过程中的尺度会发生变化，这在$SE(3)$中未能体现出来。因此，在单目情况下我们一般会显式地把尺度因子表达出来。用数学语言来说，对于位于空间的点$p$，在相机坐标系下要经过一个相似变换，而非欧氏变换：

         $p^{{}^{\prime }}=\left[\begin{array}{cc}sR& t\\ & \\ 0^T& 1\end{array}\right]p=sRp+t.$

在相似变换中，为我们把尺度$s$表达出来了。它同时作用在$p$的3个坐标之上，对$p$进行了一次缩放。与$SO(3)、SE(3)$相似，相似变换也对矩阵乘法构成群，称为相似变换群Sim(3)：

         $Sim(3)=\left\{\begin{array}{c}S=\left[\begin{array}{cc}sR& t\\ & \\ 0^T& 1\end{array}\right]\in {\mathbb{R}}^{4\times 4}\end{array}\right\}$

  同样地，Sim(3)也有对应的的李代数、指数映射、对数映射等。李代数$\mathfrak{sim}(3)$元素是一个7维向量$\zeta$。它的前6维与$\mathfrak{se}(3)$相同，最后多了一项$\sigma$。

         $\mathfrak{sim}(3)=\left\{\begin{array}{c}\zeta |\zeta =\left[\begin{array}{c}\rho \\ \\ \varphi \\ \\ \sigma \end{array}\right]\in {\mathbb{R}}^7,{\zeta }^{\wedge }=\left[\begin{array}{cc}\sigma I+{\varphi }^{\wedge }& \rho \\ & \\ 0^T& 0\end{array}\right]\in {\mathbb{R}}^{4\times 4}\end{array}\right\}$

  它比$\mathfrak{se}(3)$多了一项$\sigma$。关联Sim(3)和$\mathfrak{sim}(3)$的仍是指数映射和对数映射。指数映射为

         $\exp ({\zeta }^{\wedge })=\left[\begin{array}{cc}{e}^{\sigma }\exp ({\varphi }^{\wedge })& J_s\rho \\ & \\ 0^T& 1\end{array}\right].$

  其中，$J_s$的形式为

         $\begin{array}{rl}{J}_s& =\frac{e^{\sigma }-1}{\sigma }I+\frac{\sigma e^{\sigma }\sin \theta +(1-e^{\sigma }\cos \theta )\theta }{{\sigma }^2+{\theta }^2}{a}^{\wedge }\\ & +\left(\frac{e^{\sigma }-1}{\sigma }-\frac{(e^{\sigma }\cos \theta -1)\sigma +(e^{\sigma }\sin \theta )\theta }{{\sigma }^2+{\theta }^2}\right)a^{\wedge }{a}^{\wedge }.\end{array}$

  通过指数映射，我们能够找到李代数与李群的关系。对于李代数$\zeta ,$它与李群的对应关系为

         $s=e^{\sigma },R=\exp ({\varphi }^{\wedge }),t=J_s\rho .$

  旋转部分和SO(3)是一致的。平移部分，在$\mathfrak{se}(3)$中需要乘一个雅可比$\mathcal{J},$而相似变换的雅可比更复杂雅克比更复杂。对于尺度因子，可以看到李群中的$s$即为李代数中的$\sigma$的指数函数。
  Sim(3)的BCH近似与SE(3)是相似的。我们可以讨论一个点$p$经过相似变换$Sp$，相对于$S$的导数。同样地，存在微分模型和扰动模型两种方式，而扰动模型较为简单。我们省略推导过程，直接给出扰动模型的结果。设给予$Sp$左侧一个小扰动$\exp ({\zeta }^{\wedge }),$并求$Sp$对于扰动的导数。因为$Sp$是4维的齐次坐标，$\zeta$是7维向量，所以该导数应该是$4\times 7$的雅可比。方便起见，记$Sp$的前3维组成向量为$q,$那么：

         $\frac{\partial Sp}{\partial \zeta }=\left[\begin{array}{ccc}I& -q^{\wedge }& q\\ & & \\ 0^T& 0^T& 0\end{array}\right]$

4.6 小结

  本讲引入了李群SO(3)和SE(3)，以及它们对应的李代数$\mathfrak{so}(3)$和$\mathfrak{se}(3)。$我们介绍了位姿在它们上面的表达和转换，然后通过BCH的线性近似，就可以对位姿进行扰动并求导。这给之后讲解位姿的优化打下了理论基础，因为我们需要经常对某一个位姿的估计值进行调整，使它对应的误差减小。只有在弄清楚如何对位姿进行调整和更新之后，才能继续后续的内容。
  值得一提的是，除了李代数，同样也可以用四元数、欧拉角等方式表示旋转，只是后续的处理要麻烦一些。在实际应用中，也可以使用SO(3)加上平移的方式来代替SE(3)，从而回避一些雅可比的计算。