误差与误差分析

一、数学原理
由分部积分法得递推公式: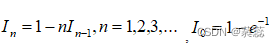 在这里插入图片描述

逆推公式：在这里插入图片描述

积分公式：f=@(x) x.^n.*exp(x-1);
I(n)=integral(f,0,1); %integral为matlab的积分函数
画图函数：plot(x,y1,x,y2,x,y3)

二、实验内容
本实验通过编写代码，在matlab或python中实现以下要求。
计算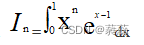在这里插入图片描述
(n=15,16,17,18,19,20)，将结果填入下表中，分析误差，并画出当n=2、5、8时，该积分对应的几何图形,使用matlab脚本文件实现。

n	15	16	17	18	19	20
正推法
真值
逆推法

代码部分：

clc,format compact
N=20;
I=zeros(3,N);   
I0=1-exp(-1);  
I(1,1)=1-I0;
f=@(x) x.^1.*exp(x-1);
I(2,1)=integral(f,0,1);

for n=2:N
    I(1,n)=1-n*I(1,n-1); 
    f=@(x) x.^n.*exp(x-1);
    I(2,n)=integral(f,0,1);
end
%逆推法
In1= (1+exp(-1))/(N+1)/2 ;      
I(3,N)=(1-In1)/(N+1);
for n=N-1:-1:1     
    I(3,n)= (1-(I(3,n+1)))/(n+1);  
end

x= 0:  0.01  : 1;   
y1=x.^2.*exp(x-1);
y2=x.^5.*exp(x-1);
y3=x.^8.*exp(x-1);
plot(x,y1,x,y2,'-.',x,y3,'*') 
legend('n=2','n=5','n=8'),grid on,xlabel('定积分 0-1'),ylabel('In')
%在坐标区上添加图例
title('积分对应的几何含义图形')

三、通用操作步骤
⑴. 双击matlab图标，或者直接双击已存在的M文件，进入编辑界面，如下图所示。注意：应将当前文件夹设置到M文件所在的路径。
图1-1

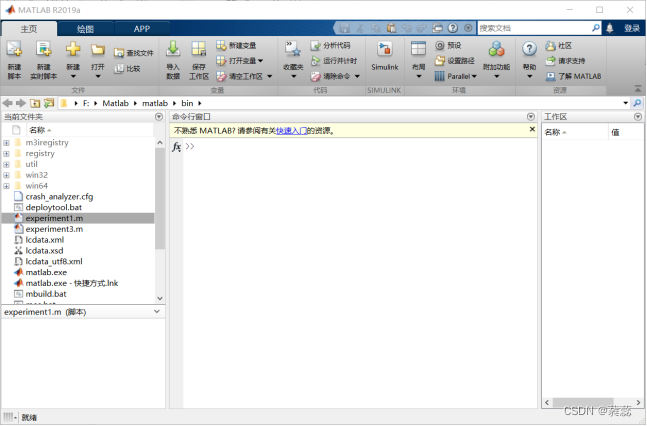
⑵.新建脚本文件或函数文件：在新建菜单项中点击下拉箭头，选择脚本或函数，即可实现。注意：函数文件的名称需要和函数名称一致。
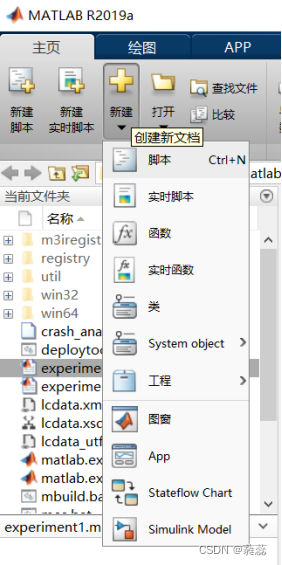
在这里插入图片描述

⑶.脚本文件在编写完成后，直接点击运行按钮，即在命令行窗口得到运行结果。
在这里插入图片描述

⑷函数文件在编写完成后，需要在命令行窗口输入命令，回车确认后，程序即可运行。注意：函数名称与函数文件一致。
在这里插入图片描述

四、实验结果与分析
下图为实验不同计算方法的部分计算结果对比图，中间一行为真值，第一行为正推法，第三行为逆推法。其数值在程序成功运行后，在matlab界面的工作区，点击符号“I”可查看。

n	15	16	17	18	19	20
正推法	0.0590	0.0555	0.0572	-0.0295	1.5596	-30.1924
真值	0.0590	0.0557	0.0528	0.0501	0.0477	0.0455
逆推法	0.0590	0.0557	0.0528	0.0501	0.0477	0.0461

上表的数据说明：当n=18及以上时，正推法计算结果明显错误。原因在于正推公式中初始数据的误差在每次计算时顺次乘以n=1,2, …而传播累积到In中，使得I18明显计算错误。而逆推法的累积误差是以倍数1/n减少的，所以结果比较精确。
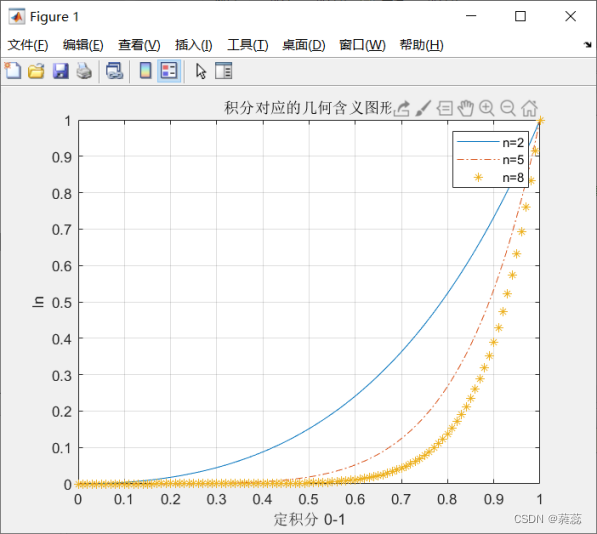
在这里插入图片描述

上图显示了积分曲线的绘制结果，其步长为0.01。从图中可以看出随着n的增加，其积分数值必然是递减的，趋近于0，但一定大于0。

猜你喜欢