树上倍增法求LCA

LCA有三种求法，在此处只介绍树上倍增法求LCA。
首先介绍LCA,它表示树上最近公共祖先，如下图，5与1的最近公共祖先是2，5与3的公共祖先有2，3，1，但是其中3是最近的公共祖先，再如1与6的最近公共祖先是7.
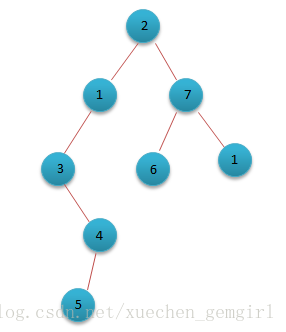
这里写图片描述
如求5与1的最近公共祖先时，我们可以先让5网上爬到与1在同一个深度3，然后再一起往上爬，直至爬到共同的点2即可结束。但这样爬的效率不是很高，可以让往上爬的速度加快，如何加快，在这里需要用到每次爬2^i。
具体算法实现如下步骤：
一，先指定一个点为根节点，进行深搜，确定每个点在树上的深度。如图以2号节点为根节点深搜后深度值情况：
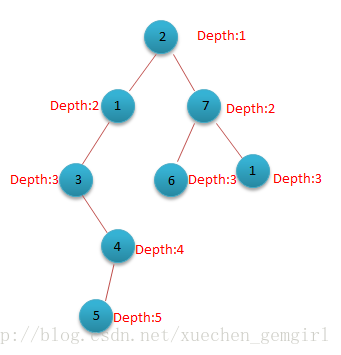
这里写图片描述
程序代码如下：

void dfs(int u){
    for(int i = head[u];i;i = edge[i].next){
        int v = edge[i].to;
        if(v!= a[u][0]){
            a[v][0] = u;   //记录父节点
            dept[v] = dept[u] + 1;
            dfs(v);
        }       
    }
}

二、用类似ST表中的初始化过程的倍增思想来记录父节点。本篇中用a数组来记录，a[i][0]记录的是i节点的父节点，a[i][j] 记录i点的往上2^j层的祖先节点编号。如图：
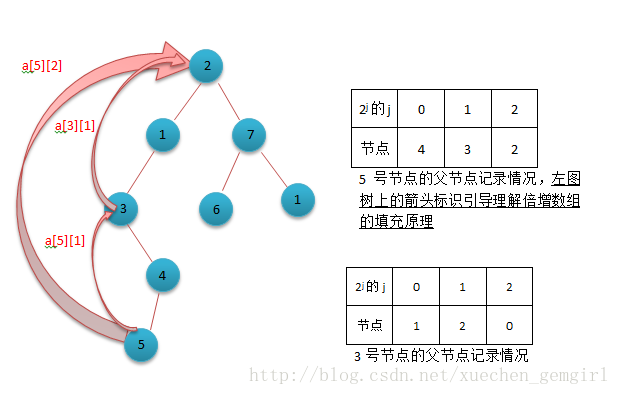
这里写图片描述
那么a[i][j]=a[a[i][j-1]][j-1];
因此此处初始化程序代码为：

void bzinit(){
    for(int i = 1;(1<<i) <= n; i++ ){
        for(int j = 1; j<= n;j++){
            a[j][i] = a[a[j][i-1]][i-1];
        }
    }
}

三、（u，v）中让深度深的点往上爬到与另一点相同深度。
深度差值即为深度较深的点需要爬的距离。利用二进制的思想跳跃的爬，如深度差值为5，由于5 的二进制是101，因此只需要先爬2^0即1层，然后再爬2^2即4层，即可让其向上爬5层。具体到上图中（5，1）中，5与1的深度差是2，因此只需要2^1层，即向上爬到a[5][1]处，也就是3节点处。具体实现代码：

if(dept[x]< dept[y]) swap(x,y);
    int t = dept[x] - dept[y];
    for(int i =0;(1<<i) <= t;i++){
        if(t & (1<<i)){  //按位找是1的位
            x = a[x][i];
        }
    }

四、接下来就是同时往上爬了，一个点地一个点地跳很浪费时间，如果一下子跳到目标点内存又可能不支持，相对来说倍增的性价比算是很高的，　倍增的话就是一次跳2^i 个点，如果即将跳到相同就不跳，如果跳到不同的节点就往上跳，否则不跳，从大步往小步跳。
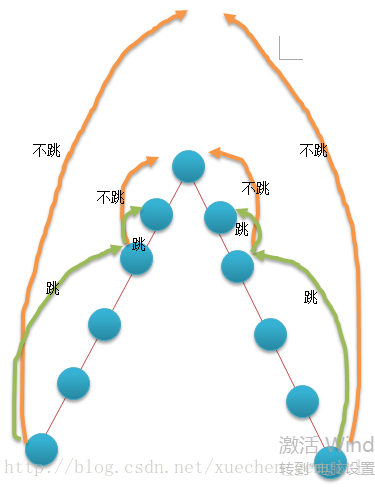
这里写图片描述
程序代码如下：

    if(x == y) return x;   //特殊的如果y是x的父节点，则在第三步中即会跳至y处。
    for(int i= N ;i>=0;i--){//此处N为(1<<N)>n的最小整数。
        if(a[x][i] != a[y][i]){//不同则跳，相同则不跳。
            x = a[x][i];
            y = a[y][i];
        }
    }
    return a[x][0];

理解上面四步后，下面查看洛谷上LCA模板题的完整代码：

#include<iostream>
using namespace std;
int n,m,s,N;
struct node{
    int to,next;
};
node edge[1000002]; 
int cnt,head[500002];
int fa[500002],dept[500002],a[500002][23];

void add(int u,int v)
{
    edge[++cnt].to = v; edge[cnt].next = head[u];head[u] = cnt;
}
void dfs(int u)
{
    for(int i = head[u];i;i = edge[i].next)
    {
        int v = edge[i].to;
        if(v!= a[u][0])
        {
            a[v][0] = u;
            dept[v] = dept[u] + 1;
            dfs(v);
        }       
    }
}
int log2(int x)
{
    int i;
    for( i=1;(1<<i) <= n;i++ );
    return i;
}
void bzinit(){
    for(int i = 1;i <= N ; i++ ){
        for(int j = 1; j<= n;j++){
            a[j][i] = a[a[j][i-1]][i-1];
        }
    }
}
int lca(int x,int y)
{
    if(dept[x]< dept[y]) swap(x,y);
    int t = dept[x] - dept[y];
    for(int i =0;(1<<i) <= t;i++)
    {
        if(t & (1<<i)){
            x = a[x][i];
        }
    }
    if(x == y) return x;
    for(int i= N ;i>=0;i--)
    {
        if(a[x][i] != a[y][i]){
            x = a[x][i];
            y = a[y][i];
        }
    }
    return a[x][0]; 
}
int main()
{
    int x,y;
    cin >> n >> m >> s;
    N = log2(n);
    for(int i = 1;i<= n-1; i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    dept[s] = 1;a[s][0]=0;
    dfs(s);
    bzinit();
    for(int i =1; i<= m;i++)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",lca(x,y));        
    }
    return 0;
 }

猜你喜欢