MATLAB常见非线性可视化绘制方法-相图与相空间（二维线性相图与非线性相空间）

本文首发于 matlab爱好者 微信公众号，欢迎关注。

惯例声明：本人没有相关的工程应用经验，只是纯粹对相关算法感兴趣才写此博客。所以如果有错误，欢迎在评论区指正，不胜感激。本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。

0 引言

本文大概介绍一下常用的非线性可视化的方法，由于篇幅问题，决定分两篇介绍，第一篇介绍一下相图与相空间的概念。第二篇介绍一下庞加莱截面和分岔图的绘制方法。后面第三篇就不打算写可视化了，看看要不要写一个频谱分析、李雅普诺夫指数分析、维数分析之类的时间序列分析（挖坑，继续挖坑）。

非线性的数学研究诞生时间还是比较久了，从蝴蝶效应开始一直到现在，常用的分析方法变化不是太大。各领域研究方向有所不同，但在论文中如果涉及到方程的非线性，总会需要定性的分析一下，由于方法比较类似，所以常常也可以参阅别的领域的非线性分析相关的方法或者好看的绘图方式。

第二篇博客链接如下：
MATLAB常见非线性可视化绘制方法-分岔图与庞加莱截面（混沌可视化、Poincare截面、Logistic、Henon、Lorenz、Rossler、Duffing系统）https://blog.csdn.net/weixin_42943114/article/details/123462050

之前有四篇文章介绍了非线性的一些有趣特性，感兴趣的可以跳转查看：
利用matlab进行混沌摆仿真（双摆、三摆、多摆演示）https://blog.csdn.net/weixin_42943114/article/details/121891553

利用matlab实现复数域空间牛顿迭代法的分形图案展示（newton法）https://blog.csdn.net/weixin_42943114/article/details/121905957

Mandelbrot集Julia集分形的MATLAB实现（分形艺术）https://blog.csdn.net/weixin_42943114/article/details/122814900

利用matlab实现三体问题（双星、3星、多星运动）https://blog.csdn.net/weixin_42943114/article/details/106616411

参考目录
[1]Morris W. Hirsch. 微分方程、动力系统与混沌导论[M]. 人民邮电出版社, 2008.
[2]刘秉正. 非线性动力学与混沌基础[M]. 东北师范大学出版社, 1994.
[3] Khalil H K . 非线性系统(第3版)[M].电子工业出版社,2005.
[4]Morris W. Hirsch. Differential equations, dynamical systems, and an introduction to chaos [M] Academic Press
[5] 微分方程、动力系统与混沌导论[M]
[6] 计算物理基础-第10章第77讲（北京师范大学）（中国大学MOOC）计算物理基础_北京师范大学_中国大学MOOC(慕课) (icourse163.org)
[7]Computing accurate Poincaré maps[J]. PHYSICA D, 2002, 171(3):127-137.
[8]Santo Banerjee. Applications of Chaos and Nonlinear Dynamics in Engineering[M]. Springer, 2011
[9]Ali.H.Nayfeh. Applied Nonlinear Dynamics Analytical, Computational, and Experimental Methods[M]. 1995.(用到了P284里面的Henon系统)
[10]詹姆斯·格雷克. 混沌：开创新科学[M].

1 简单二阶微分方程

首先什么是非线性？那就是除了线性系统，都是非线性系统。所以要想认识非线性系统有什么不同，就要首先理解线性系统的特点，才能对比看出非线性系统的特性。

1.1 最简单的线性系统

我们用一个烂大街的弹簧线性系统为例。弹簧的力为f=-kx，与小方块的位移有关。阻尼器的力为f=-cdx，dx是小方块的速度。

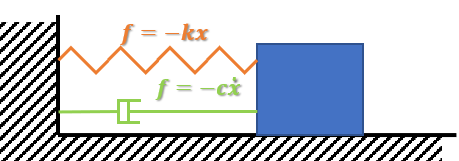
此时，小方块的加速度可以用牛二律F=ma求解出来：
$$-kx-c\dot{x}=m\ddot{x}$$
这里之后为了方便，假设m=1。

由于里面含有二阶导，不方便分析。因此为了方便后续的数学分析，我们把方程整理为下面的形式：

$${\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{c}\dot{x}\\ -kx-c\dot{x}\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -k& -c\end{array}\right]\ast \left[\begin{array}{c}x\\ \dot{x}\end{array}\right]$$

这里列向量元素有2个，因此叫做2阶微分方程。我们把这种可以整理称x’=Ax形式的微分方程，叫做线性方程，其中A是一个常数矩阵。微分方程的所有信息都包含在了矩阵A中，因此我们便建立起了微分方程与线性代数之间的关系。具体的关系，我们在第二章相图中介绍。

1.2 简单的非线性系统

对于上面的方程，如果稍加改造，将阻尼器换为空气阻尼，即f=-c*dx^2，也就是和速度的平方有关。则方程将可以改写做：
$${\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{c}\dot{x}\\ -kx-c{\dot{x}}^2\end{array}\right]$$
此时方程将无法写成 x’=Ax 的形式，所以这个方程是非线性的。此时线性系统的分析方式将全部失效。

可以看到线性系统是多么的宝贵而特殊的形式。

1.3 简单的时变系统

刚才我们在1.1节中，矩阵A是一个常数矩阵，这代表今天质量块的运动特性，和明天质量块的运动特性是相同的，不会因为时间改变而变化。这种情况我们称系统是时不变系统，即不随时间变化的系统。

如果弹簧会逐渐生锈，k的值会随时间变化，我们则称这个系统为时变系统。今天测量质量块的运动特性和第二天测量的特性会有些区别。但是如果把时间放的比较短，也就是每一瞬时，系统仍然是线性的。

如果再加一个非线性外部扰动力f(t)，则系统将会彻底进入非线性时变系统。（这里感谢@weixin_43957890在评论区提出的修改意见）其形式为：
$${\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{c}\dot{x}\\ -kx-c\dot{x}-f(t)\end{array}\right]$$
或者也可以写作：
$${\left[\begin{array}{c}x\\ \dot{x}\\ f\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{c}\dot{x}\\ -kx-c\dot{x}-f\\ f^{\prime }(t)\end{array}\right]$$

2 线性系统相图

首先咱还是先回到下面这个 x’=Ax 的弹簧模型上：
$${\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{cc}0& 1\\ -k& -c\end{array}\right]\ast \left[\begin{array}{c}x\\ \dot{x}\end{array}\right]$$

2.1 相图的引入

我们取k=0.925，c=0.3，代入到上面的现象方程中，取不同的初始x，可以得到下面几组解：

线性系统代表的矩阵A为：
$$\left[\begin{array}{cc}0& 1\\ -0.925& -0.3\end{array}\right]$$
矩阵A的特征根为λ1=-0.15+0.95i，λ2=-0.15-0.95i。特征值的实部都是负数，代表系统收敛。特征值的虚部不为零，存在震荡现象。

如果我们并不关心其时间上究竟什么时间是波峰，什么时间是波谷，我们更关心这个系统是否收敛，系统是否震荡的话，那么还有另一套方法来研究这个系统，那就是相图。

相图或相空间(phase space)其实名字起得很玄乎，但是实际很简单，就是绘制出变量和变量导数的关系。举个例子，平时我们都画位移时间x-t图，但是相图这里要画位移速度x-v图。

上面的曲线绘制成相图形式，如下：

可以看到这3条曲线都汇聚到了(0,0）这个点，代表最终这三种情况都会收敛，而且收敛的时候速度和位移都是0。不停的绕圈，则证明这三种情况都是震荡的。我们把这种画在相空间里线叫做轨线。

这三条曲线形态如此的一致，仿佛背后有一种力场在约束着曲线的运动。那怎么反推出背后的场呢？我们还要回到初始的方程来看。
在绘制出某个时间t1时刻的点[x1,dx1]后，下一个时间t2的点[x2,dx2]。根据流场的理论，该点的速度为：
$$\frac{[\begin{array}{c}x2\\ dx2\end{array}]-[\begin{array}{c}x1\\ dx1\end{array}]}{t2-t1}=[\begin{array}{c}x\\ dx\end{array}{]}^{{}^{\prime }}$$
因此，我们就可以求得每一个点对应的速度，来构建出速度场。在已知系统的方程时，这个速度场非常好构建，就是变量的导数。因此这种场也是相图的一种表现形式。

因为轨线的相当于整个流场中的一根流线，所以知道相空间，也就知道了相空间内每一根轨线的行为。也就可以反推出时域图上系统运动的特性。
由于轨线受场的约束，所以一些场论的结论也可以直接用到轨线上。比如轨线永远不会交叉，不会凭空消失。轨线的起点和终点只可能是：绘图边界以及源（发散点）、汇（吸引点）（或鞍点之类的）。这个具体的行为，在之后的章节会慢慢涉及到。

代码如下：

clear
clc
close all
%线性系统，用来展示相空间的用途
%小阻尼震荡（负实，共轭虚部）
A=[0,1;
    -0.925,-0.3];
%大阻尼震荡（负实，无虚部）
% A=[0,1;
%     -0.96,-2];
%只有阻尼（一个为0一个为负）
% A=[0,1;
%     0,-2];
%只有弹簧（实部都为0）
% A=[0,1;
%     -1,0];
%鞍点
% A=[0.15,0;
%     0,-0.15];

[y,dy,u,v]=PhaseSpace_Linear(-5:0.05:5,-4:0.05:4,A);%构建线性系统相空间的流场

h=1e-2;
x0=0:h:20;
N=length(x0);
%相同的微分方程，不同的初始状态
[y1,~]=ODE_RK4_hyh(x0,h,[4;-2],A);%计算微分方程，这里也可以用ode45
[y2,~]=ODE_RK4_hyh(x0,h,[0;-4]+[0.5;0],A);
[y3,~]=ODE_RK4_hyh(x0,h,[-3;3]+[1;0],A);
%绘制时域图
figure()
hold on
plot(x0,y1(1,:),'color',[1,0,0])
plot(x0,y2(1,:),'color',[0,1,0])
plot(x0,y3(1,:),'color',[0,0,1])
%绘制箭头
xy_lim=axis;
xy_ratio=get(gca, 'DataAspectRatio');xy_ratio=xy_ratio(1:2);
N_Arrow=5;
for k=1:N_Arrow
    N_k=round(N/N_Arrow*(k-0.83));
    plot_arrow( xy_lim,xy_ratio,[x0(N_k),y1(1,N_k)]...
        ,[1,0,0],1, [x0(N_k)-x0(N_k-10),y1(1,N_k)-y1(1,N_k-10)] )
   plot_arrow( xy_lim,xy_ratio,[x0(N_k),y2(1,N_k)]...
        ,[0,1,0],1, [x0(N_k)-x0(N_k-10),y2(1,N_k)-y2(1,N_k-10)] )
    plot_arrow( xy_lim,xy_ratio,[x0(N_k),y3(1,N_k)]...
        ,[0,0,1],1, [x0(N_k)-x0(N_k-10),y3(1,N_k)-y3(1,N_k-10)] )
end
hold off
legend("条件1","条件2","条件3")
box on
xlabel('t');ylabel('x');
%绘制相图
figure()
hold on
plot(y1(1,:),y1(2,:),'color',[0.8,0,0],'linewidth',1);%位移和速度曲线
plot(y2(1,:),y2(2,:),'color',[0,0.8,0],'linewidth',1)
plot(y3(1,:),y3(2,:),'color',[0,0,0.8],'linewidth',1)
xlim([-5,5]);ylim([-4,4])
%绘制箭头
xy_lim=axis;
xy_ratio=get(gca, 'DataAspectRatio');xy_ratio=xy_ratio(1:2);
N_Arrow=3;
for k=1:N_Arrow
    N_k=round(N/N_Arrow*(k-0.9));
    plot_arrow( xy_lim,xy_ratio,[y1(1,N_k),y1(2,N_k)]...
        ,[0.8,0,0],2, [y1(1,N_k)-y1(1,N_k-10),y1(2,N_k)-y1(2,N_k-10)] )
    plot_arrow( xy_lim,xy_ratio,[y2(1,N_k),y2(2,N_k)]...
        ,[0,0.8,0],2, [y2(1,N_k)-y2(1,N_k-10),y2(2,N_k)-y2(2,N_k-10)] )
    plot_arrow( xy_lim,xy_ratio,[y3(1,N_k),y3(2,N_k)]...
        ,[0,0,0.8],2, [y3(1,N_k)-y3(1,N_k-10),y3(2,N_k)-y3(2,N_k-10)] )
end
hold off
xlim([-5,5]);ylim([-4,4])
box on
xlabel('x');ylabel('dx');

% figure()
hold on
h=streamslice(y,dy,u,v);%叠加上之前求解出的流场效果
xlim([-5,5]);ylim([-4,4])
box on
xlabel('x');ylabel('dx');

function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识
%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数
A=Input;
F=A*y;
Output=[];
end

function [y,dy,u,v]=PhaseSpace_Linear(y1,y2,A)
[y,dy]=meshgrid(y1,y2);%初始化网格
u=zeros(size(y));v=u;
for k=1:numel(y)
    %计算网格上每一个点的上的方向
    F=Fdydx(0,[y(k);dy(k)],A);
    u(k)=F(1);
    v(k)=F(2);
end
end

function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
    yn=y(:,ii);
    xn=x(ii);
    [K1,~]=Fdydx(xn    ,yn       ,Input);
    [K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
    [K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
    [K4,~]=Fdydx(xn+h  ,yn+h*K3  ,Input);
    y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end

function plot_arrow(xy_lim,xy_ratio,xy_arrow,arrow_color,arrow_width,arrow_direction)
%初始化箭头形状（归一化的形状）
arrow_0=[0,0;-1,0.5;-1,-0.5];
%对方向进行归一化
a_dn=arrow_direction(:)./xy_ratio(:);
a_dn=a_dn/sqrt(sum(a_dn.^2));
d=(xy_lim(4)-xy_lim(3)+xy_lim(2)-xy_lim(1))/2;
%箭头对窗口缩放
arrow_1=arrow_0*arrow_width*0.03*d;
%箭头旋转
arrow_2=arrow_1*[a_dn(1),a_dn(2);-a_dn(2),a_dn(1)];
%箭头变形
xy_ratio_n=xy_ratio/sqrt(sum(xy_ratio.^2));%对比例尺归一化
arrow_3=arrow_2.*xy_ratio_n+xy_arrow;
fill(arrow_3(:,1),arrow_3(:,2),arrow_color,'EdgeColor','none')
end

2.2 线性系统的定性分析

介绍了相空间的绘制方法，那么如果改变不同的矩阵A，会出现什么样的结果呢？
其实这主要也和矩阵A的特征根有关。对于二阶系统，找到了特征根，就找到了其系统特征。

下图简单绘制了常见二阶系统的相图以及时域图。绘图代码还是上一小节的代码，改一下矩阵A就好。

这里我举的例子基本都是收敛的例子。当矩阵特征根的实部为正数时，就会发散，这个很好改，就不演示了。
咱就大概按照顺序解说一下：

1 震荡收敛
之前提到过了，就是特征根为负，存在虚部。常见于欠阻尼系统。
我们管此时相图上的中心点为螺旋点。

2 不震荡收敛
特点为特征根为负，但是不存在虚部。因此收敛过程不会有震荡线性。常见于过阻尼系统。
我们管此时相图上的中心点为结点。

3 不确定收敛点的收敛
特点为特征根一个是0。以图为例，质量块不存在弹簧，只是在粗糙地面上自由滑行。初始速度和位置不确定，则质量块滑到哪里算哪里，不会在一个固定位置上停下。但是我们可以知道其收敛的时候，速度一定等于0。
当然，这个直线不一定是水平的，只是我举的例子比较特殊。

4 无阻尼震荡
特点为所有根的实部都是0。这样系统就不存在收敛或发散，只有虚部代表的震荡。

5 鞍点
特点为特征根一个为正，一个为负。表现为轨线先被该点吸引，然后再远离该点。实际物理上，可以用一个马鞍面的山来比喻，一个小球从山顶滚落，到了山谷，然后从山谷又落到了更底层。
所以通常鞍点虽然是方程的某个特殊解，但是由于其不稳定性，很难在现实中测量到。
就像单摆的最高点，理论上是个静力的平衡点，但是如果做动力学分析，就会发现是一个不稳定的鞍点。所以速度大的时候，单摆总会倾向于向着最高点运动，但是真正到了最高点，又会由于其不稳定而离开。不像最低点，是一个收敛的稳定的结点，是单摆最终的归宿。

3 非线性系统相图

说完了线性系统的相图，我们也举一个一般情况一点的非线性系统相图。
这里先举一个《非线性系统》[见参考文献3]上面的例子。
$$\begin{gathered} \dot{x_1}=0.5(-h(x_1)+x_2) \\ \dot{x_2}=0.2(-x_1-1.5x_2+1.2) \\ h(x)=83.72x^5-226.31x^4+229.62x^3-103.79x^2+17.76x \end{gathered}$$
该方程是一个非线性方程，也可以用相同的方式，求解出每一个点处的x1和x2的导数，然后绘制出相图。

由于非线性系统在任意根的附近，都可以局部线性化，所以第2章中涉及到的线性系统知识依然可以用到非线性系统中。

比如上面那个图，依然可以看到三个特殊的点，两个稳定的结点和一个鞍点。

绘图代码如下：

[y,dy]=meshgrid(-0.5:0.02:1.5,-0.5:0.02:1.5);%初始化网格
u=zeros(size(y));v=u;
for k=1:numel(y)
    %计算网格上每一个点的上的方向
    F=Fdydx(0,[y(k);dy(k)],1);
    u(k)=F(1);
    v(k)=F(2);
end
figure()
streamslice(y,dy,u,v,4)
xlabel('y')
ylabel('dy')
box on


function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识
%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数
switch Input
    %示例1
    case 1
        p=[83.72,-226.31,229.62,-103.79,17.76,0];
        dy(1)=0.5*(-polyval(p,y(1))+y(2));
        dy(2)=0.2*(-y(1)-1.5*y(2)+1.2);
        F=[dy(1);dy(2)];
    %示例2
    case 2
        dy(1)=y(2);
        dy(2)=-y(1)+0.3*(1-y(1)^2)*y(2);%0.3
        F=[dy(1);dy(2)];
end
Output=[];
end

4 三维系统相空间

高维系统通常也用二维相平面来表示，下面举两个例子来说明。（本章只是演示更高维度的相空间与轨线，不涉及新的可视化）

4.1 线性三阶系统

对于更高阶的线性系统，单独的一个二维相平面就无法去准确的描述了，需要用更高维度的向量场去描述。也就是高维的相空间。
举个例子，下面一个三维的一个相空间如图所示：

这样并不方便观察系统的特性。
所以通常即使是高维度的系统，也往往只绘制2维相平面，然后在2维相平面上观察系统特性。

上面绘图的简单代码如下

clear
clc
close all
D=[-1+1i,0,0;0,-1-1i,0;0,0,-1];
V=[[0.5;-0.2+0.5i;0.3],[0.5;-0.2-0.5i;0.3],[0.2;0.3;0.4]];
A= V*D*inv(V);
A=real(A);%构建一个3维线性系统
[x1,x2,x3]=meshgrid(-1.5:0.05:1.5,-1.5:0.05:1.5,-1.5:0.05:1.5);%初始化网格
u=zeros(size(x1));v=u;w=u;%开始计算相空间
for k=1:numel(x1)
    %计算网格上每一个点的上的方向
    F=Fdydx(0,[x1(k);x2(k);x3(k)],A);
    u(k)=F(1);
    v(k)=F(2);
    w(k)=F(3);
end
hcone = coneplot(x1,x2,x3,u,v,w,...
    x1(1:9:end,1:9:end,1:9:end),x2(1:9:end,1:9:end,1:9:end),x3(1:9:end,1:9:end,1:9:end),8);
hcone.FaceColor = 'red';
hcone.EdgeColor = 'none';
camlight right
lighting gouraud
% set(hsurfaces,'AmbientStrength',0.6)
hcone.DiffuseStrength = 0.8;
view(3)
axis equal vis3d

function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识
%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数
A=Input;
F=A*y;
Output=[];
end

4.2 高阶时变系统

下面介绍一个时变系统的方程，还是最开头提到的弹簧模型，但是加了一个周期力。
$${\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{c}\dot{x}\\ -kx-c\dot{x}-\sin (2t)\end{array}\right]$$
因为它是时变系统，所以无法绘制出场形态的相平面图，只能绘制出轨线形式的相图。
可以看到轨线有交叉，这是典型的高阶系统的特征。

但是这种轨线的交叉，可以解释为在某些高维相空间中的不交叉轨线，投影到二维平面上。比如上面的方程可以改写做：
$${\left[\begin{array}{c}x\\ \dot{x}\\ f\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{c}\dot{x}\\ -kx-c\dot{x}-f\\ 2\cos (2t)\end{array}\right]$$
此时相空间变为：

所以上面那个二维相图，相当于这个三维相图在x3方向上投影，投影到x1x2平面上。

clear
clc
close all
%演示1
h=2e-2;
x0=0:h:40;
N=length(x0);
[y1,~]=ODE_RK4_hyh(x0,h,[0.5;0.5],1);
figure()
plot(x0,y1(1,:),'color',[1,0,0])
figure()
plot(y1(1,:),y1(2,:),'color',[1,0,0])
%演示2
[y2,~]=ODE_RK4_hyh(x0,h,[0.5;0.5;0],2);
figure()
plot(x0,y2(1,:),'color',[1,0,0])
figure()%三维立体
plot3(y2(1,:),y2(2,:),y2(3,:),'color',[0,0,0])
xlabel('x1');ylabel('x2');zlabel('x3');
hold on
box on
plot3(y2(1,:),y2(2,:),y2(3,:)*0-1,'color',[1,0,0])
%引入理论结果：
x=x0;
y_theory=5/78*cos(2*x)+25/78*sin(2*x)+...
    exp(-0.15*x).*(6647/15249*cos(sqrt(391)/20*x)-59*sqrt(391)/15249*sin(sqrt(391)/20*x));
figure()
plot(x0,y1(1,:),x,y_theory);legend('数值计算','理论解')

%后置函数
function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识
%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数
if Input==1
dy1=y(2);
dy2=-y(1)-0.3*y(2)-sin(2*x);
F=[dy1;dy2];
elseif Input==2
dy1=y(2);
dy2=-y(1)-0.3*y(2)-y(3);
dy3=2*cos(2*x);
F=[dy1;dy2;dy3];
end
Output=[];
end

function [y,Output]=ODE_RK4_hyh(x,h,y0,Input)
%4阶RK方法
%h间隔为常数的算法
y=zeros(size(y0,1),size(x,2));
y(:,1)=y0;
for ii=1:length(x)-1
    yn=y(:,ii);
    xn=x(ii);
    [K1,~]=Fdydx(xn    ,yn       ,Input);
    [K2,~]=Fdydx(xn+h/2,yn+h/2*K1,Input);
    [K3,~]=Fdydx(xn+h/2,yn+h/2*K2,Input);
    [K4,~]=Fdydx(xn+h  ,yn+h*K3  ,Input);
    y(:,ii+1)=yn+h/6*(K1+2*K2+2*K3+K4);
end
Output=[];
end

但是注意，这种轨线的交叉并不意味着非线性，事实上，上面这个系统可以被认为是线性的。这是一个典型的带阻尼受迫振动，并能够给出相应的解的：
$$\begin{gathered} y(t)=\frac{5}{78}(5\sin (2t)+\cos (2t)) \\ +e^{-\frac{3t}{20}}\frac{6647\cos \left(\frac{\sqrt{391}t}{20}\right)-59\sqrt{391}\sin \left(\frac{\sqrt{391}t}{20}\right)}{15249} \end{gathered}$$
对应的导数和轨线方程也可以利用公式计算得到（本人借助Mathematica）。

5 非线性相图的特征

下面几个特征是非线性相图才会出现的。

5.1 多个平衡点

之前在第3章已经介绍了一个。这里再介绍一个单摆方程：
$$\ddot{\theta }+\sin \theta =0$$
绘制相图为：

可以看到这个相图由许多同心圆和鞍点组成。

3Blue1Brown之前做过一个很漂亮的可视化，来讲解这个相图与微分方程之间的联系，感兴趣的可以去看一下：
https://www.bilibili.com/video/BV1tb411G72z

5.2 极限环

极限环只会出现在二维非线性系统中，在相图中表现为，其收敛位置并不是某一个点，而是一个圆环。
举个Van der Pol方程的例子：
$${\left[\begin{array}{c}x\\ \dot{x}\end{array}\right]}^{{}^{\prime }}=\left[\begin{array}{c}\dot{x}\\ -x-ϵ(1-x^2)\dot{x}\end{array}\right]$$
当$ϵ=0.3$时，相图上会出现一个极限环：

整个空间只有一个平衡点，即极限环内部发散的螺旋点。为了直观的了解极限环的特性，选取不同的初始条件，对方程进行时域的求解，得到下面的结果：

在极限环外的点，刚开始呈现出收敛的波形，但是随后振幅保持恒定。在极限环里面的点，刚开始呈现出发散的波形，但是随后振幅也保持稳定。两者都被空间中的极限环所吸引，进行周而复始的画圈圈运动中。

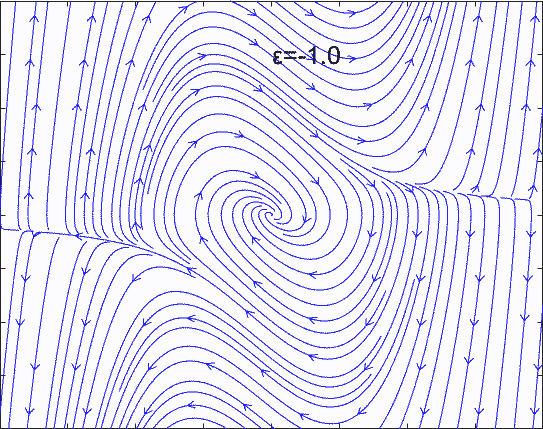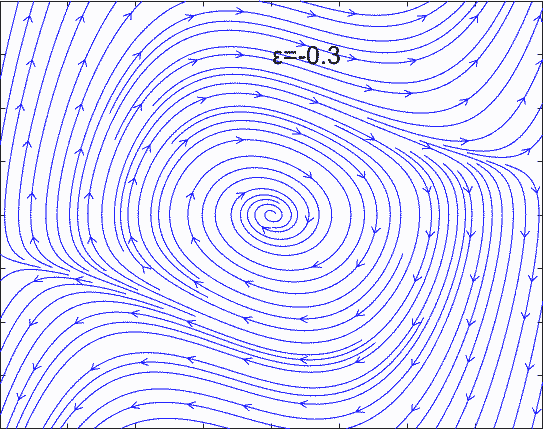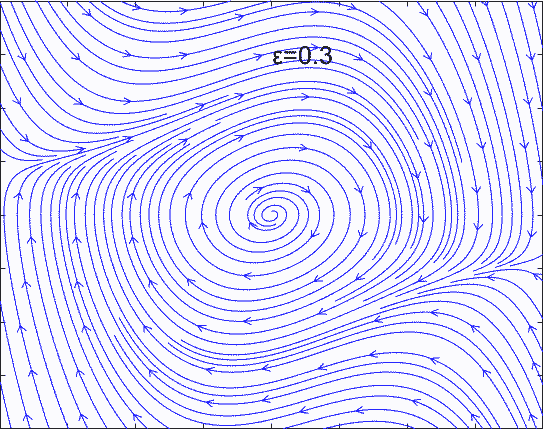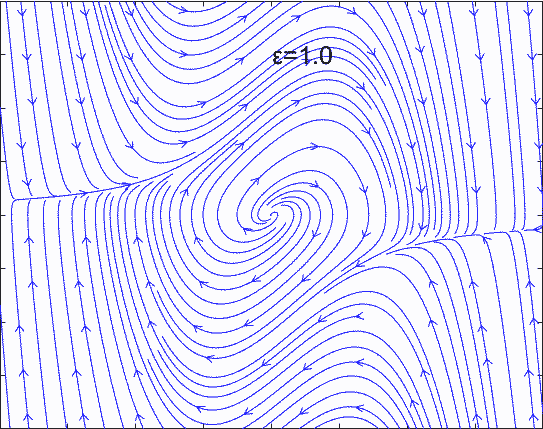
如果方程中某些系数发生变化（比如上面方程的ε由负变为正），会导致整个相空间发生改变。这种改变会使得平衡点性质发生变化，导致整个系统的性质发生变化，我们称系统在这个位置发生了分岔。比如Van der Pol方程的ε由负变为正，平衡点由稳定变为发散，导致空间中稳定位置由一个点变为一个运动的极限环。

单摆方程和Van der Pol方程的绘图代码如下：

clear
clc
close all
%1单摆模型
[x1,x2]=meshgrid(-6:0.05:6,-2:0.05:2);%初始化网格
u=zeros(size(x1));v=u;w=u;
for k=1:numel(x1)
    %计算网格上每一个点的上的方向
    F=Fdydx(0,[x1(k);x2(k)],1);
    u(k)=F(1);
    v(k)=F(2);
end
figure()
h=streamslice(x1,x2,u,v);
ylim([-2,2]);
%2极限环
[x1,x2]=meshgrid(-4:0.02:4,-4:0.02:4);%初始化网格
u=zeros(size(x1));v=u;w=u;
for k=1:numel(x1)
    %计算网格上每一个点的上的方向
    F=Fdydx(0,[x1(k);x2(k)],2);
    u(k)=F(1);
    v(k)=F(2);
end
figure()
h=streamslice(x1,x2,u,v);
ylim([-4,4]);

function [F,Output]=Fdydx(x,y,Input)
%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识
%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数
if Input==1
dy1=y(2);
dy2=-sin(y(1));
F=[dy1;dy2];
elseif Input==2
    dy1=y(2);
    dy2=-y(1)+0.3*(1-y(1)^2)*y(2);%0.3
    F=[dy1;dy2];
elseif Input==3
end
end

5.3 混沌

混沌现象表现在二维相图上，就是看上去一团乱麻，缺少规律。因为涉及到轨线交叉，所以必然维度要大于2维。因此，混沌现象必然在三维或者更高维度才产生。

分析混沌和分岔，需要用到庞佳莱截面和分岔图，这个具体放在下一篇文章中讲。

5.4 其它

如果试验测量的振动数据，用相图来分析的话，可以比较直观的看出其振动特征。

如果振动相图比较接近圆或者椭圆，比如第1个图，则证明系统有较好的线性特征，可以考虑从线性方程的角度去简化系统。
如果振动相图是个非圆图形，比如第2个图，则需要考虑其非线性。如果振动即使受到干扰，也可以比较稳定的保持在一个振幅和频率，则可以从二维极限环来建立系统模型。
如果振动轨线出现了交叉，比如第3个图，则可以从高维方程、倍周期分岔等角度进行分析。
如果振动出现了杂乱无章，由隐隐有些规律，则可以从混沌角度去分析。

相图由于涉及到对信号求导得到dy，所以如果系统的噪声太大，则相图效果会比较差。因为高频噪声求导的数值要大于低频信号求导的数值（sin(5x)求导为5cos(5x)，是sin(x)的5倍）。所以遇到较大噪声的系统，建议先进行滤波，再进行相图绘制。

比如下图，就是同样的信号，上面是原始带噪声的信号，下面是滤波后的信号。可以看出如果不滤波，即使很小的噪声都会严重干扰相图的形状。

上图演示用的代码如下：

clear
clc
close all
[t,y]=ode45(@Fdydx,0:0.01:20,[2;0]);
%模拟加噪声的信号
y1=y(:,1)+0.02*randn(size(y(:,1)));

%1直接求导，绘制相图
dy1=diffhyh(y1,1)/(t(2)-t(1));
figure()
plot(y1,dy1)
ylim([-6,6])
figure()
plot(t,y1)
%2滤波后求导，绘制相图
[b,a]=butter(6,0.04*2,'low');
y2=filtfilt(b,a,y1);
dy2=diffhyh(y2,1)/(t(2)-t(1));
figure()
plot(y2,dy2)
ylim([-6,6])
figure()
plot(t,y2)
function [F]=Fdydx(x,y)
%形式为Y'=F(x,Y)的方程，参见数值分析求解常系数微分方程相关知识
%高次用列向量表示，F=[dy(1);dy(2)];y(1)为函数，y(2)为函数导数
dy1=y(2)+0.01*randn();
dy2=-y(1)+0.9*(1-y(1)^2)*y(2)+0.01*randn()+0.01*sin(4*x);%这里直接在系统中加噪声
F=[dy1;dy2];
end
function Fdiff=diffhyh(F,dim)
%采用2阶中心差分，边缘采用一阶向前或向后差分（边缘没有搞迎风差分，精度要求不高）
%dim，差分的维度方向，dim=1对应着矩阵向下方向的差分，dim=2对应的向右
diffF1=diff(F,1,dim);
if dim==1%向下
    Fdiff=([zeros(1,size(F,2));diffF1]+[diffF1;zeros(1,size(F,2))])/2;
    Fdiff(1,:)=diffF1(1,:);
    Fdiff(end,:)=diffF1(end,:);
elseif dim==2%向右
    Fdiff=([zeros(size(F,1),1),diffF1]+[diffF1,zeros(size(F,1),1)])/2;
    Fdiff(:,1)=diffF1(:,1);
    Fdiff(:,end)=diffF1(:,end);
end
end

一些常用的简单滤波方法可以参见这篇博客：
几种常用信号平滑去噪的方法 https://blog.csdn.net/weixin_42943114/article/details/107693068

6 简单离散迭代系统的表示

除了上面的微分方程会出现非线性线性，一些离散系统同样会出现非线性。
比如
$$\left[\begin{array}{c}{x}_{n+1}\\ y_{n+1}\end{array}\right]=\left[\begin{array}{c}\sin (1\ast x_{n+1})+\cos (2\ast y_{n+1})\\ \sin (2\ast x_{n+1})-\cos (1\ast y_{n+1})\end{array}\right]$$
经过多次迭代，可以得到下面的图像：

这种混乱无序而又隐隐存在规律的特点，正是混沌现象。

下一章我们便从离散系统的分岔与混沌开始讲起，来引入分岔图的概念。由于篇幅限制，相关内容将另开一篇文章，敬请期待。

上图的绘图代码：

y0=[0.5;0.5];
N=1e6;
y=zeros(size(y0,1),N);
y(:,1)=y0;
for k=1:N-1
    yk1=y(:,k);
    yk2=[sin(1*yk1(1))+cos(2*yk1(2));
        sin(2*yk1(1))-cos(1*yk1(2))];
    y(:,k+1)=yk2;
end
scatter(y(1,:),y(2,:),3,'Marker','.','MarkerEdgeColor','k','MarkerEdgeAlpha',0.1)