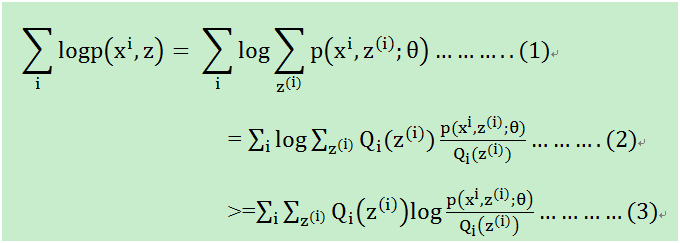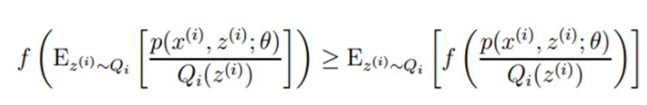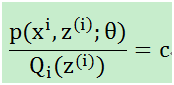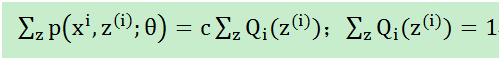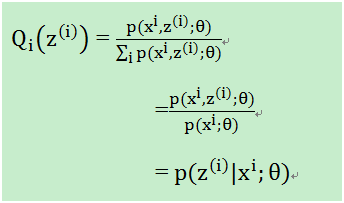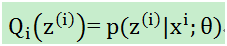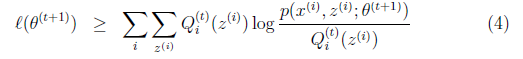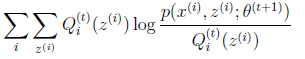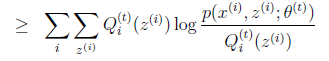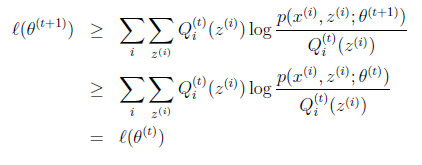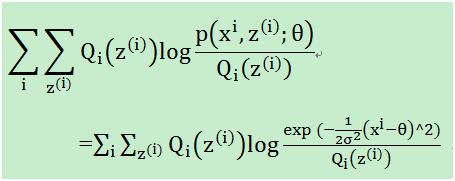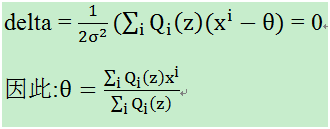最大似然估计

这篇文章主要是在我后续添加的参考文献中总结和概括出来的，如有雷同，肯定是我抄他。谢谢。

先看个例子：

你妈妈给你提了一篮子"好"鸡蛋，假设里面有100个"独立的"鸡蛋，你从里面挑出10个，然后你称的鸡蛋的重量分别是:10.0kg，10.1kg，10.2kg，10.2kg，9.9kg，9.9kg，10.2kg，10.3kg，10.1kg，9.8kg.(好重的鸡蛋)。然后要你去估计一个"好"鸡蛋大概是多重？

这里先有个假设：鸡蛋重量服从高斯分布m~(u,sigma).u是均值，sigma是方差。

由于你是从100个鸡蛋里面随便拿出来的，从你的角度来看这些鸡蛋之间是没有关系的。那么，你从篮子那么多鸡蛋中为什么就恰好抽到了这10个鸡蛋呢？抽到这10个鸡蛋的概率是多少呢？因为这些鸡蛋（的身高）是服从同一个高斯分布p(x|θ)的。那么你抽到鸡蛋A（的身高）的概率是p(x_A|θ)，抽到鸡蛋B的概率是p(x_B|θ)，由于他们是独立的，所以很明显，你同时抽到鸡蛋A和鸡蛋B的概率是p(x_A|θ)* p(x_B|θ)，同理，我同时抽到这10个男生的概率就是他们各自概率的乘积了。用数学家的口吻说就是从分布是p(x|θ)的总体样本中抽取到这10个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示

这里n=10,因为这里的x是我们能够观察到的，因此x是已知量。学过概率论的同学知道，为了使得上式最大化，对θ求导，令导数为0，就可以得到θ了。

假设我们计算得到的θ=10kg。

某位同学与一位猎人一起外出打猎，一只野兔从前方窜过。只听一声枪响，野兔应声到下，如果要你推测，这一发命中的子弹是谁打的？你就会想，只发一枪便打中，由于猎人命中的概率一般大于这位同学命中的概率，看来这一枪是猎人射中的。

这个例子所作的推断就体现了极大似然法的基本思想
最大似然估计到EM

假设你妈妈给你提了两篮子鸡蛋，一篮子"好"鸡蛋，一篮子"坏"鸡蛋。每个篮子100个鸡蛋。你从"好"篮子里面挑出10个鸡蛋，称重量分别是: 10.0kg，10.1kg，10.2kg，10.2kg，9.9kg，9.9kg，10.2kg，10.3kg，10.1kg，9.8kg;然后你从"坏"篮子里面也挑出10个，称重量分别是5.0kg，5.1kg，5.2kg，5.2kg，4.9kg，4.9kg，5.2kg，5.3kg，5.1kg，4.8kg。

按照上面最大似然估计，你都可以计算"好"篮子鸡蛋和"坏"篮子鸡蛋的平均重量。

假设你计算完之后得出:"好"鸡蛋平均重量10kg，"坏"鸡蛋平均重量5kg。

以上妈妈都是好妈妈！

如果你妈妈提了一篮子鸡蛋，里面既有"好"鸡蛋也有"坏"鸡蛋，而且只有"好"鸡蛋和"坏"鸡蛋。现在要你估计一下一种鸡蛋和另外一种鸡蛋的平均重量！你会说我又不知道哪些蛋属于第一个高斯分布，哪些属于第二个，所以就没法估计这两个分布的参数。反过来，你会觉得只有当我对这两个分布的参数作出了准确的估计的时候，才能知道到底哪些蛋属于第一个分布，那些蛋属于第二个分布。

把每个蛋看作是三元组y_i={x_i,z_i1,z_i2}，其中，xi是第i个样本的观测值(你能称的重量)。zi1和zi2表示"好"蛋和"坏"蛋这两个高斯分布中哪个被用来产生值xi，就是说这两个值标记这个蛋到底是"好"蛋还是"坏"蛋（的重量分布产生的）。确切的说，z_ij在xi由第j个高斯分布产生时值为1，否则为0。例如一个样本的观测值为10.1kg，然后你来自好的那个高斯分布，那么你可以将这个样本表示为{10.1, 1, 0}。如果zi1和zi2的值已知，也就是说每个蛋你已经标记为"好"蛋和"坏"蛋了，那么你就可以利用上面说的最大似然算法来估计他们各自高斯分布的参数。但是它们未知，因此你只能用EM算法。

但问题是你不知道z_ij，怎么办？

做法是你假设已经知道了这个是"好"蛋，虽然是没有理由的假设，但是你可以先根据这个假设给这个分布整一个初始值，然后用这个期望当成已知量，这一下就只有一个自变量了，你可以根据最大似然估计得到该分布的参数，那假设这个参数比之前的那个随机的参数要好，它更能表达真实的分布，那么你再通过这个参数确定的分布去求这个隐含变量的期望，然后再最大化，得到另一个更优的参数，……迭代，就能得到一个皆大欢喜的结果了。
EM算法推导

假设有样本集,其中是m个独立的样本,每个样本对应的类别z⁽ⁱ⁾是不知道的(不知道是好鸡蛋还是坏鸡蛋)，要估计概率模型p(x,)的参数(估计坏鸡蛋的重量),但是由于z我们也不知道，那么就不能使用最大似然估计。那如果知道了z，就好计算了。

目标是求等式(1)左边的最大值,

等式(1): 对每一个样本i的所有可能类别z求等式右边的联合概率密度函数和，也就得到等式左边为随机变量x的边缘概率密度.

如果对等式(1)进行求导,即log(f1(x)+log(f2(x))+.....)，很麻烦，于是有等式(2)的变形

等式(2):分子分母同乘一个不为0的数

等式(3):变成和的对数

插播

Jensen不等式:

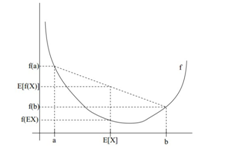
如上图是一个凸函数,凸函数定义是什么:

设f是定义域为实数的函数，如果对于所有的实数x。如果对于所有的实数x，f(x)的二次导数大于等于0，那么f是凸函数。当x是向量时，如果其hessian矩阵H是半正定的，那么f是凸函数。如果只大于0，不等于0，那么称f是严格凸函数

如果f是凸函数，X是随机变量，那么：E[f(X)]>=f(E[X])

如果f是凹函数，X是随机变量，那么：E[f(X)]<=f(E[X])

辅助记忆:y=x²是凸函数，y=-x²是凹函数

如等式(3)中是概率p(x),是x，是log(x)，这是个凹函数。

因此等式(2)中的就是期望(E(X)=∑x*p(x)，f(X)是X的函数，则E(f(X))=∑f(x)*p(x)),而且概率和，因此对照凹函数的E[f(X)]<=f(E[X])

以及(2)式，可以得到(3)式,模式如下。

但是.......

由于我们要得到(2)式的最大值，(2)和(3)式之间却是个不等式。咋办？我不断的增加(3)式的最大值，是不是相应的让(2)取得的值会更大？水涨船高的原理，你想一想是不是这么个理儿！

是的！

似然函数L(θ)>=J(z,Q)，那么我们可以通过不断的最大化这个下界J，来使得L(θ)不断提高，最终达到它的最大值，如下图所是:

图1

我先让θ固定，下界J(z,Q)它只能跑到上图蓝色的地方，因为他的最大值是红色的L(θ)，然后我再固定Q(z),这个时候调整θ，使得J(z,Q)最大，如下如到了θ^t+1;然后重复上述动作，直至收敛。

在上述(1)式到(2)式中，我们凭空添加了个Q！

那么这个Q根据什么来选择？

对于上图而言，当θ固定，下界J(z,Q)它只能跑到上图蓝色的地方，(2)式和(3)式是相等的。按照这个思路，我们要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，这里得到：

分母乘过去,

至此，我们计算出了的概率(在知道θ和样本时，该样本来自于z⁽ⁱ⁾的概率)，即在固定θ时，为了让(2)式和(3)式相等，即下界拉升(跑到上图1蓝色位置)。这是第一步即E，接下来就是L(θ)的最大化下界J(z,Q)，即调整θ，使得J(z,Q)最大，即步骤M:

θ = maxJ(z,Q)

将J(z,Q)展开就是

上面E步骤和M-步骤，就是EM算法。

对于图1而言，

我们为啥能知道一定能收敛？

当

Jensen不等式相等，这是在θ^t时刻，那么在θ^t+1时刻呢？我们要最大化的极大似然是

L(θ^t+1)有:

上面不等式(4)的右边，就是上式(1)-上式(3)么？

我们在θ^t时刻，让下界J(z,Q)最大化的时候，让θ变化，从θ^t跳到θ^t+1时刻么，这步不就是M的步骤么？于是有:

上面不等式的右边就是L(θ^t)。

合起来就是:

So:到这儿，EM算法的推导算是结束了。

EM例子和python代码

例子: 模拟两个正态分布的均值估计

由于我们使用的是高斯分布，即p服从高斯分布。在上述M-step中，我们要最大化如下式子:

这里的θ是我们要估计的均值。

然后对这个求导：

接下来是简单的Python代码:

#! /usr/bin/env python
#! -*- coding=utf-8 -*-

#模拟两个正态分布的均值估计

from numpy import *
import numpy as np
import random
import copy

SIGMA = 6
EPS = 0.0001
#生成方差相同,均值不同的样本
def generate_data():	
	Miu1 = 20
	Miu2 = 40
	N = 1000
	X = mat(zeros((N,1)))
	for i in range(N):
		temp = random.uniform(0,1)
		if(temp > 0.5):
			X[i] = temp*SIGMA + Miu1
		else:
			X[i] = temp*SIGMA + Miu2
	return X

#EM算法
def my_EM(X):
	k = 2
	N = len(X)
	Miu = np.random.rand(k,1)
	Posterior = mat(zeros((N,2)))
	dominator = 0
	numerator = 0
	#先求后验概率
	for iter in range(1000):
		for i in range(N):
			dominator = 0
			for j in range(k):
				dominator = dominator + np.exp(-1.0/(2.0*SIGMA**2) * (X[i] - Miu[j])**2)
				#print dominator,-1/(2*SIGMA**2) * (X[i] - Miu[j])**2,2*SIGMA**2,(X[i] - Miu[j])**2
				#return
			for j in range(k):
				numerator = np.exp(-1.0/(2.0*SIGMA**2) * (X[i] - Miu[j])**2)
				Posterior[i,j] = numerator/dominator			
		oldMiu = copy.deepcopy(Miu)
		#最大化	
		for j in range(k):
			numerator = 0
			dominator = 0
			for i in range(N):
				numerator = numerator + Posterior[i,j] * X[i]
				dominator = dominator + Posterior[i,j]
			Miu[j] = numerator/dominator
		print (abs(Miu - oldMiu)).sum() 
			#print '\n'
		if (abs(Miu - oldMiu)).sum() < EPS:
			print Miu,iter
			break

if __name__ == '__main__':
	X = generate_data()
	my_EM(X)

参考文献

http://blog.csdn.net/zouxy09/article/details/8537620/
http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

EM算法原理和python简单实现

最大似然估计

最大似然估计到EM

EM算法推导

EM例子和python代码

参考文献

猜你喜欢