推导：从傅里叶级数展开到傅里叶变换

说明：本文主要参考资料为奥本海姆的《信号与系统》（第二版），推导过程中融入了少量个人理解。

假设我们已经知晓了周期信号的傅里叶级数展开，在连续信号条件下，其傅里叶级数对为

$$x\left( t \right) = \sum\limits_{k = - \infty }^{ + \infty } {{a_k}{{\rm{e}}^{ {\rm{j}}k{\omega _0}t}}} = \sum\limits_{k = - \infty }^{ + \infty } {{a_k}{{\rm{e}}^{ {\rm{j}}k\left( {2\pi /T} \right)t}}} \tag {1}$$

$${a_k} = \frac{1}{T}\int_T {x\left( t \right){{\rm{e}}^{ - {\rm{j}}k{\omega _0}t}}{\rm{d}}t} = \frac{1}{T}\int_T {x\left( t \right){{\rm{e}}^{ - {\rm{j}}k\left( {2\pi /T} \right)t}}{\rm{d}}t} \tag {2}$$

其中，公式(1)为综合公式，它描述如何将原始信号$x\left( t \right)​$分解，公式(2)为分析公式，$a_k​$表示信号$x\left( t \right)​$的傅里叶系数（也称为频谱系数），其物理意义是原始信号$x\left( t \right)​$分解出来的每一个谐波分量强度的度量，其中当$k=0​$时，即$a_0​$就是原始信号$x\left( t \right)​$的直流分量（也称为常数分量）。

类似地，在离散信号条件下，其傅里叶级数对为

$$x\left[ n \right] = \sum\limits_{k = \left\langle N \right\rangle } {{a_k}{{\rm{e}}^{{\rm{j}}k{\omega _0}n}}} = \sum\limits_{k = \left\langle N \right\rangle } {{a_k}{{\rm{e}}^{{\rm{j}}k\left( {2\pi /N} \right)n}}} \tag {3}$$

$${a_k} = \frac{1}{N}\sum\limits_{n = \left\langle N \right\rangle } {x\left[ n \right]{{\rm{e}}^{ - {\rm{j}}k{\omega _0}n}}} = \frac{1}{N}\sum\limits_{n = \left\langle N \right\rangle } {x\left[ n \right]{{\rm{e}}^{ - {\rm{j}}k\left( {2\pi /N} \right)n}}} \tag {4}$$

其中，公式(3)为综合公式，公式(4)为分析公式，其物理意义与上述连续信号类似。

扫描二维码关注公众号，回复： 1788593 查看本文章

现在我们需要将其表示傅里叶展开的手法推广到非周期信号，首先引入基本思想：

非周期信号，可以被想象成周期无穷大的周期信号。对于周期信号而言，它的周期越大，那么它的基波频率${\omega _0} = 2\pi /T$就越小，同时分解出来的各个频率分量之间的“距离”也越近，这是因为频谱图频率轴上样本的间隔为$2\pi /T$（因为在周期复指数信号${{\rm{e}}^{{\ {\rm{j}}\omega _0}t}}$中${{\omega _0}}$表示频率，相应地这里$k\left( {2\pi /T} \right)$为频率，$k$为整数，因此间隔为${2\pi /T}$），它随着周期的增大而变小。这样，在周期趋近于无穷大时，这些频率轴上的样本会越来越密，傅里叶展开由原来的许多项进行离散求和，而变为连续积分。

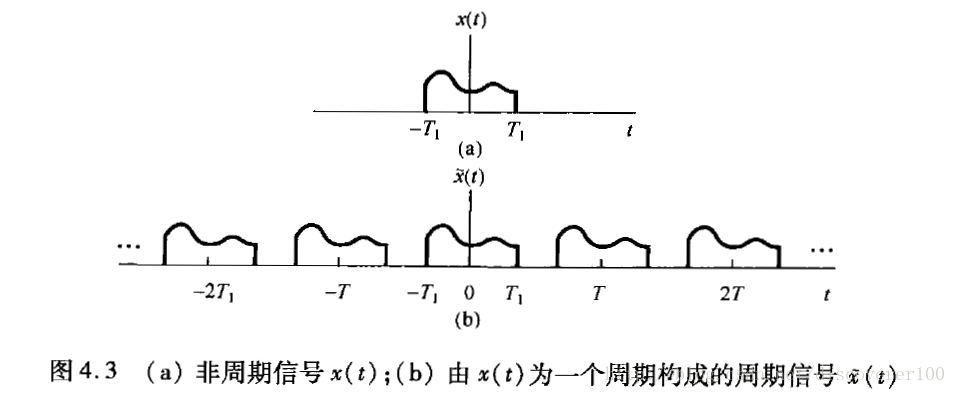
现在，我们假设有一个非周期信号$x\left( t \right)$，它具有有限的持续期，从该信号出发，可以构建一个信号$\tilde x\left( t \right)$，使得$x\left( t \right)$是$\tilde x\left( t \right)$的一个周期，这样当周期$T$无穷大时，$x\left( t \right)$就可以等于$\tilde x\left( t \right)$，由于$\tilde x\left( t \right)$是名义上的周期信号，因此我们可以先观察$\tilde x\left( t \right)$的傅里叶级数展开情况。$x\left( t \right)$和$\tilde x\left( t \right)$的函数示意图如下图所示。

将信号$\tilde x\left( t \right)$进行傅里叶展开，求解系数时，将积分区间设定为$- T/2 \le t \le T/2$，有

$$\tilde x\left( t \right) = \sum\limits_{k = - \infty }^{ + \infty } {{a_k}{{\rm{e}}^{ {\rm{j}}k{\omega _0}t}}} \tag {5}$$

$${a_k} = \frac{1}{T}\int_{ - T/2}^{T/2} {\tilde x\left( t \right){{\rm{e}}^{ - {\rm{j}}k{\omega _0}t}}{\rm{d}}t} \tag {6}$$

其中${\omega _0} = 2\pi /T$，由于当$\left| t \right| < T/2$时$x\left( t \right)=\tilde x\left( t \right)$，当$\left| t \right| \ge T/2$时$x\left( t \right)=0$，所以(6)式可以改写为

$$\begin{array}{l} {a_k} &= \frac{1}{T}\int_{ - T/2}^{T/2} {x\left( t \right){{\rm{e}}^{ - {\rm{j}}k{\omega _0}t}}{\rm{d}}t} \\ &= \frac{1}{T}\int_{ - \infty }^{ + \infty } {x\left( t \right){{\rm{e}}^{ - {\rm{j}}k{\omega _0}t}}{\rm{d}}t} \end{array} \tag {7}$$
将(7)式两边乘以 $T$，约掉等式右边的分母 $T$，有
$$T{a_k} = \int_{ - \infty }^{ + \infty } {x\left( t \right){{\rm{e}}^{ - {\rm{j}}k{\omega _0}t}}{\rm{d}}t} \tag {8}$$
对上述(8)式进行变量替换，将 $k \omega_0$替换为 $\omega$，得到 $Ta_k$的包络 $X\left( {{\rm{j}}\omega } \right)$
$$X\left( {{\rm{j}}\omega } \right) = \int_{ - \infty }^{ + \infty } {x\left( t \right){{\rm{e}}^{ - {\rm{j}}\omega t}}{\rm{d}}t} \tag {9}$$
这样，按照这种表达方式，可以重新将傅里叶系数表示为
$${a_k} = \frac{1}{T}X\left( {{\rm{j}}\omega } \right) = \frac{1}{T}X\left( {{\rm{j}}k{\omega _0}} \right) \tag {10}$$
此时，再将刚刚得到的(10)式带入(5)式，可以重新描述 $\tilde x\left( t \right)$的傅里叶展开式
$$\tilde x\left( t \right) = \sum\limits_{k = - \infty }^{ + \infty } {\frac{1}{T}X\left( {{\rm{j}}k{\omega _0}} \right){{\rm{e}}^{{\rm{j}}k{\omega _0}t}}} \tag {11}$$
又因为 $2\pi/T=\omega_0$，因此(11)式可以进一步改写为
$$\tilde x\left( t \right) = \frac{1}{{2\pi }}\sum\limits_{k = - \infty }^{ + \infty } {X\left( {{\rm{j}}k{\omega _0}} \right){{\rm{e}}^{{\rm{j}}k{\omega _0}t}}} \tag {12}$$
上文已经提及，将傅里叶变换理解为周期无穷大的特殊情形，此时的傅里叶展开会 由原来的离散求和变为连续积分，因此当 $T \to \infty$时， $\tilde x \left( t \right) \to x \left( t \right)$，上述(12)式将过渡为连续积分，并与上述公式(9)结合起来，有
$$x\left( t \right) = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {X\left( {{\rm{j}}\omega } \right){{\rm{e}}^{{\rm{j}}\omega t}}{\rm{d}}\omega } \tag {13}$$

$$X\left( {{\rm{j}}\omega } \right) = \int_{ - \infty }^{ + \infty } {x\left( t \right){{\rm{e}}^{ - {\rm{j}}\omega t}}{\rm{d}}t} \tag {9}$$

公式(13)和公式(9)就是傅里叶变换对，其中上面一行的公式(13)称为傅里叶逆变换（inverse Fourier transform），下面一行的公式(9)称为$x\left( t \right)$的傅里叶变换（Fourier transform）或傅里叶积分，$X\left( {{\rm{j}}\omega } \right)$通常称为$x\left( t \right)$的频谱。

这样，从傅里叶级数到傅里叶变换的推导就完成了。

总结：从傅里叶级数展开，到傅里叶变换，关键并不在于其中的数学推导，上述的代数推导中主要以变量替换为主，其表达方式与傅里叶级数展开并无太大区别，真正需要我们理解的是其中的思想：周期无穷大后，因为频率样本越来越密集，从而形成连续积分。明白了这一点，就不难理解傅里叶变换了。