傅里叶级数与傅里叶变换公式推导

首先，傅里叶分析是指把一个周期或非周期函数展开成一个个三角函数的叠加，如果是对其还没有基本概念的，可以看看傅里叶分析之掐死教程，这篇文章不依赖数学公式却又十分透彻地讲述了傅里叶分析的基本概念，十分值得一读。但如果先深入探讨其中的数学由来，接下来会讲述详细的数学推导。

傅里叶级数

三角函数系的正交性

三角函数系：{1,sinx,cosx,sin2x,cos2x,…,sinnx,cosnx,…}，它由无数个sinnx和cosnx组成，其中n=0,1,2,…。

正交性：
$\int^\pi_{-\pi}\sin nx \cos mx dx = 0$

$\int^\pi_{-\pi}\cos nx \cos mx dx = 0，n\neq m$

$\int^\pi_{-\pi}\sin nx \sin mx dx = 0，n\neq m$

当向量点乘等于0：
$\vec a \cdot \vec b = 0$
则两个向量正交。

拓展到函数中，两个函数相乘，原本点乘的加和变成取积分，则：
$\int^{x_1}_{x_2}f(x) g(x) dx = 0$
称为两个函数正交。

证明其正交性，可以用积化和差公式：
$\int^\pi_{-\pi}\cos nx \cos mx dx = \frac{1}{2}\int^\pi_{-\pi}[cos(n-m)x+cos(n+m)x]dx =0$
其他情况同理。

周期为2π的函数展开

因此当一个函数f(x)周期为2π时，可以展开成
$\sum^\infty_{n=0}a_ncosnx + \sum^\infty_{n=0}b_nsinnx = \frac 1 2 a_0 + \sum^\infty_{n=1}({a_ncosnx + b_nsinnx})$
对两边取积分，由于三角函数的正交性
$\int_{-\pi}^\pi f(x)dx = \frac1 2\int_{-\pi}^\pi a_0dx = \pi a_0$

$a_0 = \frac 1 {\pi}\int_{-\pi}^\pi f(x)dx$

原式乘以cos mx 再对两边取积分可得：
$\int^\pi_{-\pi}f(x) \cos mx dx = \sum^\infty_{n=1}\int^\pi_{-\pi} a_ncosnx cosmx dx = \int^\pi_{-\pi} a_ncos^2 nx dx = a_n\pi$

$a_n = \frac 1 \pi \int^\pi_{-\pi}f(x) \cos nx dx$

同理，两边同乘sinmx再取积分可得：
$b_n = \frac 1 \pi \int^\pi_{-\pi}f(x) \sin nx dx$

周期为2L的函数展开

利用换元的方法，令： $\frac \pi L t$ ，即 $\frac L \pi x$ ，可得：
$\frac {a_0} 2 + \sum^\infty_{n=1}({a_ncos \frac{n\pi}{L}t + b_nsin\frac{n\pi}{L}t})$

$a_0 = \frac 1 {L}\int_{-L}^L f(t)dt$

$a_n = \frac 1 L \int^L_{-L}f(x) \cos nx dx$

$b_n = \frac 1 L \int^L_{-L}f(x) \sin nx dx$

在工程中t总是从0开始，周期T=2L，ω = $\frac \pi L = \frac 2\pi T$ ，此时：
$\frac {a_0} 2 + \sum^\infty_{n=1}({a_ncosωt + b_nsinωt})$

$a_0 = \frac 2 {T}\int_{0}^T f(t)dt$

$a_n = \frac 2 T \int^T_{0}f(x) \cos nx dx$

$b_n = \frac 2 T \int^T_{0}f(x) \sin nx dx$

傅里叶级数的复数表达形式

欧拉公式：$ e^{iθ} = cosθ + isinθ$

可得：
$\frac 1 2 (e^{iθ}+e^{-iθ})$

$\frac 1 2 i(e^{iθ}-e^{-iθ})$

把这两条式子代入f(t)的式子中可得：
$\frac {a_0} 2 + \sum_{n=1}^\infty \frac {a_n-ib_n} 2 e^{in\omega t}+ \sum_{n=1}^\infty \frac {a_n+ib_n} 2 e^{-in\omega t} = \sum_{n=0}^0 \frac {a_0} 2 e^{in\omega t} + \sum_{n=1}^\infty \frac {a_n-ib_n} 2 e^{in\omega t}+ \sum_{n=-1}^{-\infty} \frac {a_{-n}+ib_{-n}} 2 e^{in\omega t} = \sum_{-\infty}^\infty C_n e^{in\omega t}$
当n = 0时，
$C_n = \frac {a_0} 2 = \frac 1 {T}\int_{0}^T f(t)dt$
当n > 0时，
$C_n = \frac {a_n-ib_n} 2 = \frac 1 2 (\frac 2 T \int_0^T f(t)cos{n\omega t} - i\frac 2 T \int_0^Tf(t)sin{n\omega t}) = \frac 1 T \int_0^T f(t)(cos{n\omega t} - isin{n\omega t}) dt = \frac 1 T \int_0^T f(t) e^{-in\omega t}dt$
当n < 0时，
$C_n = \frac {a_{-n}+ib_{-n}} 2 = \frac 1 T \int_0^T f(t)(cos{n\omega t} - isin{n\omega t}) dt = \frac 1 T \int_0^T f(t) e^{-in\omega t}dt$

因此得出结论，一个周期函数f(t)有f(t)=f(t+T)时：
$\sum_{-\infty}^\infty C_n e^{in\omega t}$

$C_n = \frac 1 T \int_0^T f(t) e^{-in\omega t}dt$

傅里叶变换

对于 $C_n$ 来说，它的值是一个复数，而nω是一个离散的值，那么可以在代表nω的轴上一个个特定的点上设一个平面，这个平面是一个复平面，它的长度和方向代表 $C_n$ ：
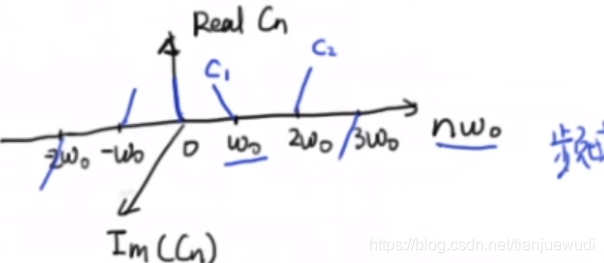
在这里插入图片描述

在工程上，横坐标为时间的波形图称为时域表达，而这幅图显示的是在各种不同频率下的值，称为频域表达，也是波形图的频谱，这就是从不同的角度看时间，每一种波形都对应一种频谱。不过很多时候的频谱都不是这种复平面三维的，我们会把 $C_n$ 的幅度即模单独拿出来，就可以表示这个函数在不同频率下的强度了。
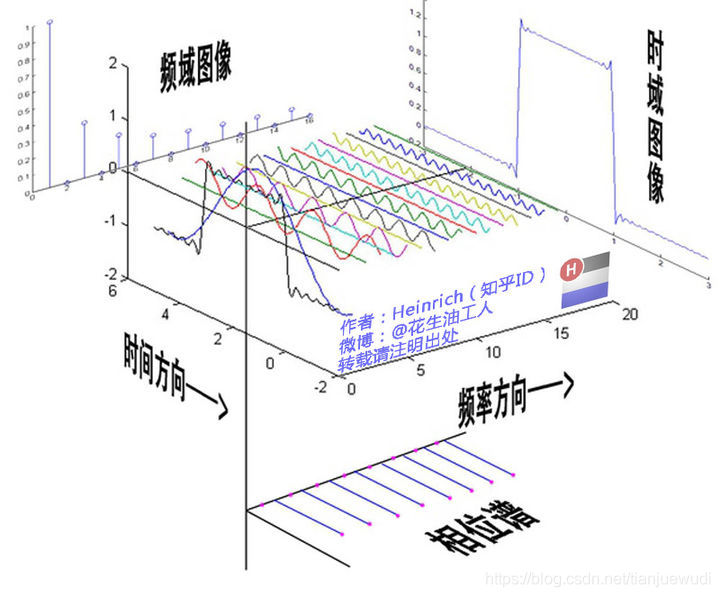
在这里插入图片描述

当T增大时，ω数值减小，nω之间就挨得越近。T趋于无穷时会形成一条连续的曲线：

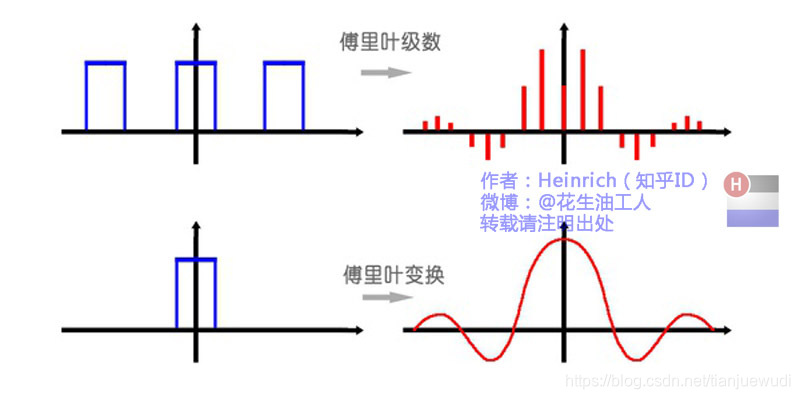
在这里插入图片描述

由：
$\sum_{-\infty}^\infty C_n e^{in\omega t}$

$C_n = \frac 1 T \int_0^T f(t) e^{-in\omega t}dt$

得到：
$f_T(t) = \sum_{n=-\infty}^{\infty}\frac 1 T \int_{-\frac T 2}^{\frac T 2} f_T(t) e^{-in\omega_0 t}dt e^{inω_0t}$

$f_T(t) = \sum_{n=-\infty}^{\infty}\frac {\Deltaω} {2\pi} \int_{-\frac T 2}^{\frac T 2} f_T(t) e^{-in\omega_0 t}dt e^{inω_0t}$

当 $\rightarrow \infty$ ：
$\frac {1} {2\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(t) e^{-i\omega t}dt e^{inωt}d\omega$
因此我们把中间的公式称为傅里叶变换(FT)：
$\int_{-\infty}^{\infty} f(t) e^{-i\omega t}dt$
通过这个函数可以表示在任何频率的情况下的三角函数的波形的振幅，这通常是一个复数a+bi，其中实数部分代表cos，虚数部分代表sin。而负频率没有现实意义，其振幅为正频率的共轭，只是为了在数学上的计算便利，实际上用 $\sqrt{a^2+b^2}$ 表示其振幅。

外面套的公式称为傅里叶变换的逆变换(IFT)：
$\frac {1} {2\pi} \int_{-\infty}^{\infty} F(ω) e^{iωt}d\omega$
傅里叶变换的所有内容讲解完毕了，傅里叶变换其实是一种特殊的拉普拉斯变换(s=iω)，遵循拉普拉斯变换的所有性质。