codeforces 964C. Alternating Sum(等比数列)

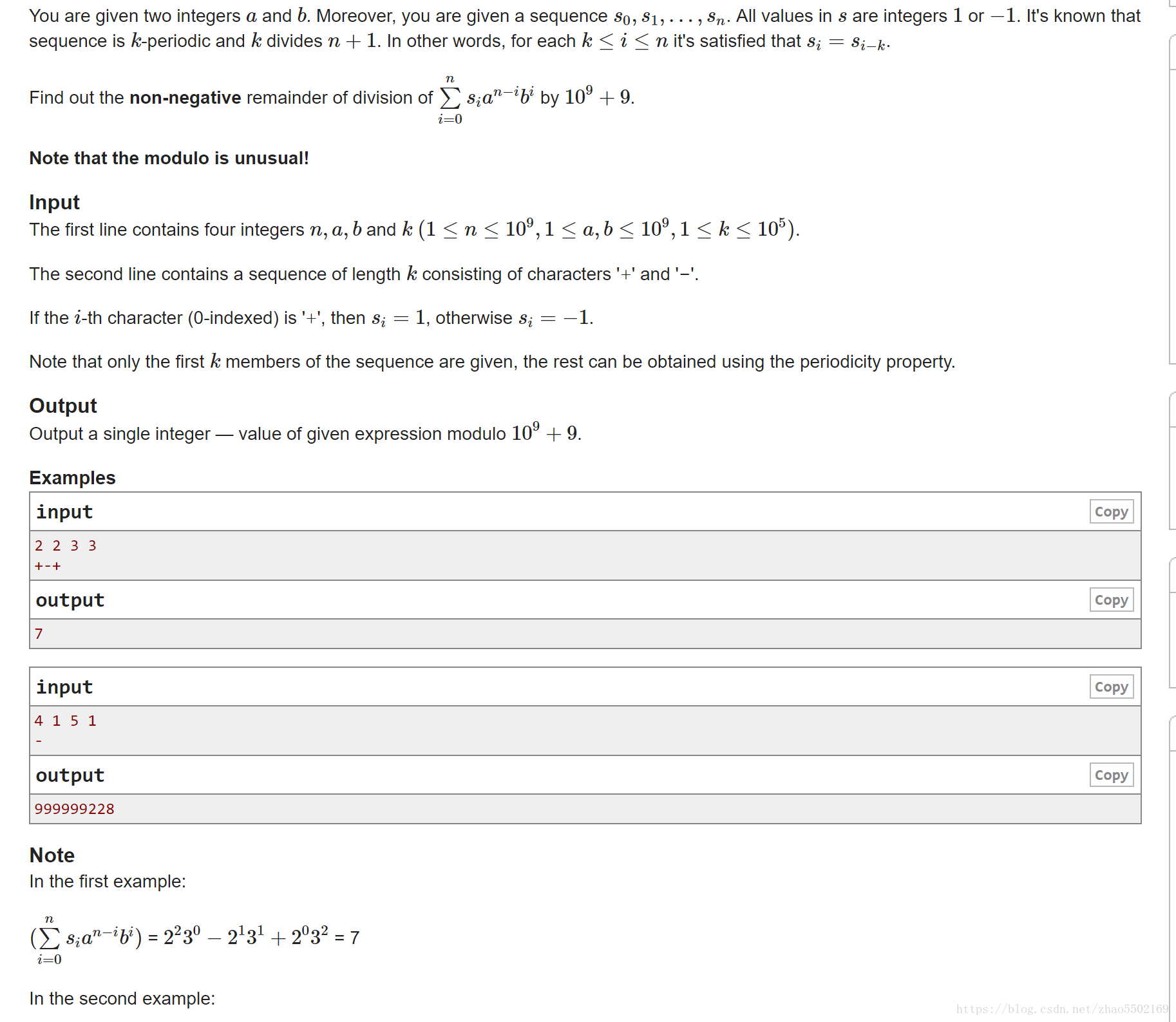
题意简单，给你一个序列s0,s1,s2…sn，共n+1个数，这个序列是满足k循环，即s[i] = s[i+k]，且这些值只可能是-1，或1，且(n+1) % k == 0。问你上图式子的和是多少。

思路：因为这个序列是满足k循环的，所以我们应该主要考虑a，b的变化，如果把这个求和公式展开后我们可以发现如果我们按k个隔开，发现他们是符合等比序列的，公比q = (b/a)^k 。所以我们可以利用等比公式来求前N项和。
而a1就是前k项的和。中间求一下逆元就行了。
代码如下：

#include<iostream>
#include<cstring>
#include<cmath>
#include<string>
#include<set>
#include<map>
#include<vector>
#include<algorithm>

using namespace std;
typedef long long ll;
const ll Mod = (ll)1e9 + 9;
const int MAX = 100010;

ll Quick_pow(ll x, ll n) {
    ll res = 1;
    while (n > 0) {
        if (n & 1)  res = res * x % Mod;
        x = x * x % Mod;
        n >>= 1;
    }
    return res;
}
char s[MAX];
ll N, a, b, k;
ll solve() {
    ll a1 = 0;
    for (int i = 0; i < k; ++i) {
        ll v = s[i] == '+' ? 1 : -1;
        a1 = (a1 + v * Quick_pow(a, N - i)*Quick_pow(b, i)%Mod+ Mod) % Mod;
        //这里要防止乘后要提前取膜，因为如果是负数两个的结果可能会很大，通过+Mod不能转换为正数。
    }
    ll Q = b * Quick_pow(a, Mod - 2) % Mod;
    Q = Quick_pow(Q, k);
    ll num = (N+1) / k;
    ll sum;
    if (Q == 1) {//注意Q为1的特殊情况
        sum = a1 * num%Mod;
    }
    else {
        sum = (a1*(Quick_pow(Q, num)-1)%Mod*Quick_pow(Q-1, Mod - 2) + Mod) % Mod;
        //这里要利用Q-1，即保证结果为正数
    }

    return sum;

}
int main(void) {
    scanf("%lld%lld%lld%lld", &N, &a, &b, &k);
    scanf("%s", s);
    printf("%lld\n", solve());
    return 0;
}