概念:
- 互质数(也叫互素):互质数为数学中的一种概念,即两个或多个整数的公因数只有1的非零自然数。公因数只有1的两个非零自然数,叫做互质数。
-
两个数a和b的最大公约数(Greatest Common Divisor)是指同时整除a和b的最大因数,记为gcd(a, b)。特殊的,当gcd(a, b) = 1,我们称a和b互素(上文略有提及)。
两个数a和b的最小公倍数(Leatest Common Multiple)是指同时被a和b整除的最小倍数,记为lcm(a, b)。特殊的,当a和b互素时,lcm(a, b) = ab。
gcd是基础数论中非常重要的概念,求解gcd一般采用辗转相除法(这个方法会下文着重介绍,这里先引出概念),而求lcm需要先求gcd,然后通过lcm(a, b) = ab / gcd(a, b)求解。这里无意中引出了一个恒等式:lcm(a, b) * gcd(a, b) = ab。这个等式可以通过算术基本定理(详见本文第三点)进行证明,证明过程可以通过图一-4-1秒懂。
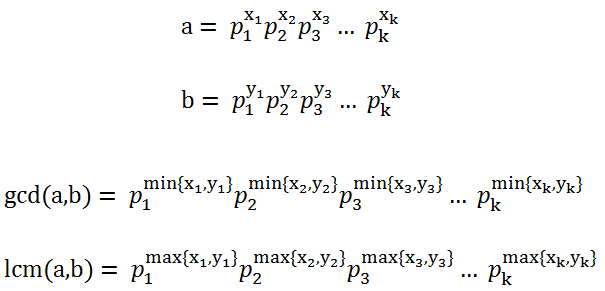
图一-4-1
需要说明的是这里的a和b的分解式中的指数是可以为0的,也就是说p1是a和b中某一个数的最小素因子,p2是次小的素因子。lcm(a, b)和gcd(a, b)相乘,相当于等式右边的每个素因子的指数相加,即min{xi, yi} + max{xi, yi} = xi + yi,正好对应了a和b的第i个素数分量的指数之和,得证。
给这样的gcd和lcm表示法冠个名以便后续使用——指数最值表示法。【例题】三个未知数x, y, z,它们的gcd为G,lcm为L,G和L已知,求(x, y, z)三元组的个数。
三个数的gcd可以参照两个数gcd的指数最值表示法,只不过每个素因子的指数上是三个数的最值(即min{x1, y1, z1}),那么这个问题首先要做的就是将G和L分别进行素因子分解,然后轮询L的每个素因子,对于每个素因子单独处理。
假设素因子为p,L分解式中p的指数为l,G分解式中p的指数为g,那么显然l < g时不可能存在满足条件的三元组,所以只需要讨论l >= g的情况,对于单个p因子,问题转化成了求三个数x1, y1, z1,满足min{x1, y1, z1} = g且max{x1, y1, z1} = l,更加通俗的意思就是三个数中最小的数是g,最大的数是l,另一个数在[g, l]范围内,这是一个排列组合问题,三元组{x1, y1, z1}的种类数当l == g时只有1种,否则答案就是 6(l - g)。
最后根据乘法原理将每个素因子对应的种类数相乘就是最后的答案了。
-
、算术基本定理
算术基本定理可以描述为:对于每个整数n(n>1),都可以唯一分解成有限个素数的乘积,如图一-3-1所示:
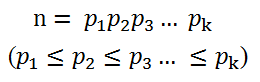
图一-3-1
这里的素数并不要求是不一样的,所以可以将相同的素数进行合并,采用素数幂的乘积进行表示,如图一-3-2所示:
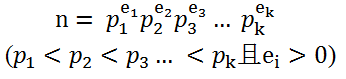
图一-3-2
证明方法采用数学归纳法,此处略去。
-
整除性
若a和b都为整数,a整除b是指b是a的倍数,a是b的约数(因数、因子),记为a|b。整除的大部分性质都是显而易见的,为了阐述方便,我给这些性质都随便起了个名字。
i) 任意性,若a|b,则对于任意非零整数m,有am|bm。
ii) 传递性,若a|b,且b|c,则a|c。
iii) 可消性,若a|bc,且a和c互素(互素的概念下文会讲到),则a|b。
iv) 组合性,若c|a,且c|b,则对于任意整数m、n,有c|(ma+nb)。
拿一个我还未出生时的初二数学竞赛题就能概括整除的性质了。
【例题】(公元1987年初二数学竞赛题) x,y,z均为整数,若11|(7x+2y-5z),求证:11|(3x-7y+12z)。
非常典型的一个问题,为了描述方便,令a = (7x+2y-5z),b = (3x-7y+12z),通过构造可以得到一个等式:3a + 4b = 11(3x-2y+3z),则4b = 11(3x-2y+3z) - 3a。
任意性+组合性,得出 11 |(11(3x-2y+3z) - 3a) = 11|4b。
可消性,由于11和4互素,得出 11 | b,证明完毕。
- 欧几里得算法(辗转相除法(Euclidean algorithm))它的具体做法是:用较小数除较大数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。
定理:gcd(a, b) = gcd(b, a % b)。
证明:a = kb + r = kb + a%b,则a % b = a - kb。令d为a和b的公约数,则d|a且d|b 根据整除(详见本文第四点)的组合性原则,有d|(a-kb),即d|(a%b)。
这就说明如果d是a和b的公约数,那么d也一定是b和a%b的公约数,即两者的公约数是一样的,所以最大公约数也必定相等。
这个函数揭示了一个约定俗成的概念,即任何非零整数和零的最大公约数为它本身。int gcd(int a, int b) //辗转相除法Code { return b==0 ? a : gcd(b,a%b); }【例题】f[0] = 0, 当n>1时,f[n] = (f[n-1]+a) % b,给定a和b,问是否存在一个自然数k (0 <= k< b),是f[n]永远都取不到的。
永远有多远?并不是本题的范畴。
但是可以发现的是这里的f[...]一定是有循环节的,如果在某个循环节内都无法找到那个自然数k,那么必定是永远都找不到了。
求出f[n]的通项公式,为f[n] = an%b,令an = kb + r,那么这里的r = f[n],如果t = gcd(a, b),r = an-kb = t ( (a/t)n - (b/t)k ),则有t|r,要满足所有的r使得t|r,只有当t = 1的时候,于是这个问题的解也就出来了,只要求a和b的gcd,如果gcd(a, b) > 1,则存在一个k使得f[n]永远都取不到,直观的理解是当gcd(a, b) > 1,那么f[n]不可能是素数。