HDU 6397 Character Encoding

题目：点击打开链接
题意： 假设有 0 到 n-1种数字，随机选取（可以重复），得到的和为k组合数量有多少种。

分析：可以用容斥或者生产函数来做。

容斥做法：

如果每个箱子里可以装的小球数量没有上限的话,答案就是（隔板法），设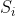为有至少有i个箱子不合法的情况（最多会有k/n个箱子不合法），答案就是

    ，

容斥原理可参考点击打开链接，讲的很好。

生成函数做法：

我们先不看k，只看n和m

当n=2时

0  1   2   3   4   5   6   7   8  9 10 11... 0   1 1   1  1 2   1  2   1 3   1  3   3   1 4   1  4   6   4   1 5   1  5  10  10   5   1 6   1  6  15  20  15   6   1 7   1  7  21  35  35  21   7   1 8   1  8  28  56  70  56  28   8   1 9   1  9  36  84 126 126  84  36   9  1 10  1 10  45 120 210 252 210 120  45 10  1 11  1 11  55 165 330 462 462 330 165 55 11  1

很显然就是杨辉三角，直接二项式定理就可以了

当n=3是，也是类似的

     0   1   2   3   4    5    6      7      8     9   10  11  12

0:  1

1:  1   1   1

2:  1   2   3    2    1

3:  1   3   6    7    6   3    1

4:  1   4  10  16  19  16  10   4      1

5:  1   5  15  30  45  51  45   30   15    5   1

6:  1   6  21  50  90 126 141 126  90  50 21  6  1

 

生成公式：

这个公式就是就可以表示第m行的结果，对应的系数就是展开式中x^i的系数，所以我们只需要求生成公式中x^k的系数即可。

那么我们就得对公式化简

根据泰勒展开：

可得

（广义二项式）

所以

到了这一步，我们就可以直接计算了，我们需要求x^k次项的系数，x^k项的系数为

可以发现容斥和生成函数推出来的公式是相同的。

代码：

#pragma comment(linker, "/STACK:102400000,102400000")
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cassert>
#include<string>
#include<cstdio>
#include<bitset>
#include<vector>
#include<cmath>
#include<ctime>
#include<stack>
#include<queue>
#include<deque>
#include<list>
#include<set>
#include<map>
using namespace std;
#define pt(a) cout<<a<<endl
#define debug test
#define mst(ss,b) memset((ss),(b),sizeof(ss))
#define rep(i,a,n) for (int i=a;i<=n;i++)
#define per(i,a,n) for (int i=n-1;i>=a;i--)
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define ll long long
#define ull unsigned long long
#define pb push_back
#define mp make_pair
#define inf 0x3f3f3f3f
#define eps 1e-10
#define PI acos(-1.0)
typedef pair<int,int> PII;
const ll mod = 998244353;
const int N = 2e5+10;

ll gcd(ll p,ll q){return q==0?p:gcd(q,p%q);}
ll qp(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
int to[4][2]={{-1,0},{1,0},{0,-1},{0,1}};

ll t,n,m,k,f[N],inv[N];

void init() {///预处理阶乘及其逆元
    f[0]=f[1]=1;
    rep(i,2,N-1) f[i]=f[i-1]*i%mod;
    inv[0]=inv[1]=1;
    rep(i,2,N-1) inv[i]=(mod-mod/i)*inv[mod%i]%mod;
    rep(i,2,N-1) inv[i]=inv[i-1]*inv[i]%mod;
}

ll C(ll n,ll m) {
    if(n<m) return 0;
    else return f[n]*inv[m]%mod*inv[n-m]%mod;
}

int main() {
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    init();
    cin>>t;
    while(t--) {
        cin>>n>>m>>k;
        ll ans=0,sig=1;
        for(int i=0;k>=i*n;i++)
            (ans += C(m,i)*C(k+m-1-i*n,m-1)*sig%mod)%=mod,sig=-sig;
        cout<<(ans+mod)%mod<<endl;
    }
    return 0;
}

参考博客：https://blog.csdn.net/njupt_lyy/article/details/81714203