FFT(坑)

作者的话

你的脸上风淡云轻，谁也不知道你的牙咬得有多紧。
你走路带着风，谁也不知道你膝盖上仍有曾摔过的伤的淤青。
你笑得没心没肺，没人知道你哭起来只能无声落泪。
要让人觉得毫不费力，只能背后极其努力。
我们没有改变不了的未来，只有不想改变的过去。
在标题的”(坑)”删除前，谢绝转载。
能不能看得懂我不知道，但我相信至少高中水平是完全没问题的(我也才初中……)
文章中不包含教学但必不可少的前置知识：
1. sin函数，cos函数，弧度制
2. 函数
3. 笛卡尔坐标系(也叫做平面直角坐标系)
4. $\sum$ 的性质

目录：

分类

缩写	全称	作用	时间复杂度
DFT	离散傅立叶变换	时频域转换	$O(n^2)$
FFT	快速傅立叶变换	时频域转换$($有精度误差$)$	$O(大常数+nlog_2n)$
NTT/FNTT	快速数论变换	模意义下的时频域转换	$O(小常数+nlog_2n)$
MTT	任意模数的NTT	任意模意义下的时频域转换	$O(nlog_2n)$
FWT	快速沃尔什变换	快速集合卷积	$O(不定)$
FMT	快速莫比乌斯变换	逆莫比乌斯反演？	$O(不定)$

快速傅立叶变换

前置知识

卷积

什么是卷积？卷积是定义在函数上的运算。下面是百度百科的定义。

卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列 $x(n)$ 和 $h(n)$，则卷积的结果为一个函数

$$y(n)=\sum_{i=-\infty}^{\infty}x(i)h(n-i)=x(n)*h(n)$$

出去的童鞋不要被百科拐跑了，百科哪有这里的文章没节操是不是…
修信号与系统的同学可能见过下面这段话：(颜色深浅似乎是CSDN的问题)

给定义在 $(-\infty,+\infty)$ 上的函数 $f_1(t)$ 与 $f_2(t)$ ，称由含参变量 $t$ 的广义积分所确定的函数

$$g(t)=\int^{+\infty}_{-\infty}f_1(τ)f_2(t-τ)\ dτ$$ 为函数 $f_1(t)$ 与 $f_2(t)$ 的卷积，记为： $$g(t)=f_1(t)*f_2(t)$$

这里最简单的一句话概括：多项式乘法实际上是多项式系数向量的卷积。
还是很晕？举个栗子吧。
设有两个多项式 $f=x^2+5x+4,g=3x^2-5x+7$。
则他们的答案 $h=f\times g=3x^4+10x^3-5x^2+15x+28$
其实是向量 $\vec f=(1,5,4),\vec h=(3,5,7)$ 的卷积为 $\vec h=\vec f\otimes \vec g=(3,10,5,15,28)$
根据多项式乘法的计算方法，可得：$h_i=\sum_i f_i\cdot g_{n-i}$。
现在再回去看百度百科的词条(就看我节选的那一段)，懂了吗？

系数表示法

设 $f(x)$ 为一个 $n$ 次函数，则其解析式为一个关于 $x$ 的 $n$ 次多项式。其解析式即为其系数表示法，也就是时域。
例：$f(x)=x^2+5x+4=(1,5,4)$
现在已知两个函数系数表示法，求这两个函数的卷积的系数表示法。
显然地，需要 $O(n^2)$ 的时间。
设有两个函数 $f(x)=x^2+5x+4,g(x)=3x^2-5x+7$。
$h(x)=f(x)\otimes g(x)$
$\qquad\,=(x^2+5x+4)\times (3x^2-5x+7)$
$\qquad\,=3x^4+10x^3-5x^2+15x+28$

点值表示法

设 $f(x)$ 为一个 $n$ 次函数，因为 $n+1$ 个点确定一条 $n$ 次函数。
因此可以选取函数上的 $n+1$ 个点来表示一个函数，称为点值表示法，也就是频域。。
例：$f(x)=\{(-1,0),(0,4),(1,10)\}$

如果已知两个函数在相同 $x$ 坐标上的点值表示法呢？求这两个函数的卷积的点值表示法。
可以很负责任地说，只需要 $O(n)$ 的时间就可以完成。
例：$f(x)=\{(-1,0),(0,4),(1,10)\},g(x)=\{(-1,15),(0,7),(1,5)\}$
则 $h(x)=f(x)\otimes g(x)$
$\qquad\quad\;=\{(-1,0),(0,4),(1,10)\}\otimes \{(-1,15),(0,7),(1,5)\}$
$\qquad\quad\;=\{(-1,0\times15),(0,4\times 7),(1,10\times 5)\}$
$\qquad\quad\;=\{(-1,0),(0,28),(1,50)\}$
可是不对啊，两个二次多项式的乘积应该是四次多项式啊，怎么能用三个点确定呢？
没错，不能用三个点确定，那我们就用更多个点来确定。
$\qquad\quad\;=\{(-2,20),(-1,0),(0,4),(1,10),(2,18)\}\otimes \{(-2,29),(-1,15),(0,7),(1,5),(2,9)\}$
$\qquad\quad\;=\{(-2,20\times 29),(-1,0\times15),(0,4\times 7),(1,10\times 5),(2,18\times 9)\}$
$\qquad\quad\;=\{(-2,580)(-1,0),(0,28),(1,50),(2,162)\}$

但是一般情况下很少使用点值表示法，因此在使用这种方法之前需要进行转换，那转换的代价是多少？$O(n^2)=O(选点n\times 计算n)$
似乎我们坠入了深渊，没关系，快速傅立叶变换能 $O(nlog_2n)$ 完成这个过程。

向量

同时具有大小和方向的量。记作 $\overrightarrow{AB}$
把$\overrightarrow{AB}=(2,3)$，画在平面直角坐标系上是：

复数

定义虚数单位 $i=\sqrt {-1}$。则形如 $a+bi$ 的数称为复数$(a,b\in R)$。
其中 $a$ 叫做实部，$b$ 叫做虚部。
在笛卡尔坐标系中，把 $x$ 轴当做实部轴，把 $y$ 轴当做虚部轴(单位长为$i$)，这样的坐标系叫做复平面。
这上图中的向量对应了复数 $2+3i$ 。

struct complex{
    double x,y;//实部和虚部 
    complex (double xx=0,double yy=0) {
        x=xx,y=yy;
    }
};

复数的辐角：即复数所表示的向量与x正半轴的夹角。如上图，$2+3i$ 的辐角为 $\theta$。特别地，若 $B$ 在x轴以下，则其辐角为其与x正半轴的夹角的相反数。

复数的运算

加法运算：实部和虚部分别相加。
例：$(3+5i)+(8-4i)=11+i$
减法运算：实部和虚部分别相减。
例：$(3+5i)-(8-4i)=-5+9i$
乘法运算：多项式乘法。
例：$(3+5i)(8-4i)=3\times8+5\times4-3\times4i+5i\times8=-44-22i$

complex operator+(complex a,complex b) {
    return complex(a.x+b.x , a.y+b.y);
}
complex operator-(complex a,complex b) {
    return complex(a.x-b.x , a.y-b.y);
}
complex operator*(complex a,complex b) {
    return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);
}

复数的”数值”

单位圆：以原点为圆心，以 $1$ 为半径画圆，所得的圆叫做单位圆。

欧拉定理：设 $B$ 为复平面上一个单位圆上的点，则 $\overrightarrow{OB}$ 所代表的复数的辐角为 $\theta$ 时，此点可以表示为 $\cos \theta+i\sin\theta$。
举个例子吧。
下图中 $\overrightarrow{AB}$ 所表示的复数为 $\cos \theta+i\sin\theta$

共轭复数

以下内容摘自百度百科。

共轭复数，两个实部相等，虚部互为相反数的复数互为共轭复数(conjugate complex number)。当虚部不为零时，共轭复数就是实部相等，虚部相反,如果虚部为零，其共轭复数就是自身。

简单来说 ，对于实数 $a$ 和实数 $b$，$a+bi$ 和 $a-bi$ 互为共轭复数。

单位根

百度百科是这样定义的。

数学上，$n$ 次单位根是 $n$ 次幂为 $1$ 的复数。它们位于复平面的单位圆上，构成正 $n$ 边形的顶点，其中一个顶点是 $1$。
$w^n=1,n\in N^*$
这方程的复数根 $w$ 为 $n$ 次单位根。

专心点，别让百科丢了你的节操。
简单来说， 以 $1$ 为起点，将单位圆 $n$ 等分，做 $n$ 个向量。
设幅角为$k\times \dfrac{360°}n(k\leqslant \dfrac n2)$的向量对应的复数为 $w_n^k$，其中 $w_n^1$ 称为 $n$ 次单位根。
幅角为$-k\times \dfrac{360°}n(\dfrac n2\leqslant k)$的向量对应的复数为 $w_n^k$。

根据欧拉公式，可得（弧度制）：
$w_n^k=\cos k\times \dfrac{2\pi}n+i\sin k\times \dfrac{2\pi}n$

单位根的性质

• $w^{2k}_{2n}=w^k_n$
  证明：$w_{2n}^{2k}=\cos 2k\times \dfrac{2\pi}{2n}+i\sin 2k\times \dfrac{2\pi}{2n}$

  $\;\qquad\qquad=\cos k\times \dfrac{2\pi}n+i\sin k\times \dfrac{2\pi}n$

  $\;\qquad\qquad=w_n^k$

• $w_n^{k+\frac{n}{2}}=-w_n^k$
  证明：$w_n^{k+\frac{n}{2}}=w_n^k\times w_n^{\frac{n}{2}}$

  $\,\quad\qquad\qquad=w_n^k\times [\cos(\dfrac n2\times \dfrac{2\pi}{n})+i\sin(\dfrac n2\times\dfrac{2\pi}{n})]$

  $\,\quad\qquad\qquad=w_n^k\times (\cos\pi+i\sin\pi)$

  $\,\quad\qquad\qquad=w_n^k\times (-1+0)$

  $\,\quad\qquad\qquad=-w_n^k$

• $ω^0_n=ω_n^n=1$

正题

某些奇奇怪怪的读法。
1. $f\bar{a}\ f\bar{a}\ t\check{a}$
2. $Fast\ Fast\ TLE$

快速傅里叶变换

显然地，一个 $n$ 次多项式可以被 $n$ 个点唯一确定。
很恶心地，FFT在取点的时候不取整数点，不取有理数点，甚至还不取实数点！而是取复数点，$n$ 次单位根的 $0$ 到 $n-1$ 次幂。
即使是这样，那时间复杂度仍然是$O(n^2)$的啊，而且复数的运算还比整数慢！
别着急，来推推柿子。
设函数 $A(x)$ 的系数为 $(a_0,a_1,a_2,...,a_{n-1})$。则有：$A(x)=\sum\limits_{i=1}^n a_ix^i$
按照下标奇偶性分类，则：

$A(x)=(a_0+a_2x^2+a_4x^4+...+a_{n-2}x^{n-2})+(a_1x+a_3x^3+a_5x^5+...+a_{n-1}x^{n-1})$

设$\,A_1(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac n2-1}$
$\quad A_2(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac n2-1}$

则有：$A(x)=A_1(x^2)+xA_2(x^2)$

这个时候，单位根终于派上用场了！
没错，我们把 $x=w_n^k (k<\frac{n}{2})$ 代入，得

$A(w_n^k)=A_1(w_n^{2k})+w_n^kA_2(w_n^{2k})$

将 $x=w_n^{k+\frac{n}{2}}$ 代入，得：

$A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}(w_n^{2k+n})$
$\qquad\qquad\,=A_1(w_n^{2k}*w_n^n)-w_n^kA_2(w_n^{2k}*w_n^n)$
$\qquad\qquad\,=A_1(w_n^{2k})-w_n^kA_2(w_n^{2k})$

发现了什么？它们互为共轭复数！
有什么作用？那么当我们在枚举第一个式子的时候，我们可以 $O(1)$ 得到第二个式子的值。
而且第一个式子的 $k$ 在取遍了 $[0,\dfrac n2-1]$ 的时候，第二个式子取遍了$[\dfrac n2,n-1]$
因此原问题的规模缩小了一半，然后呢？
分治就好啦！
下面是代码：

 void fast_fast_tle(int limit,complex *a) {
    if(limit==1)    //只有一个常数项
        return ;
    complex a1[limit>>1],a2[limit>>1];
    for(int i=0; i<=limit; i+=2)    //根据下标的奇偶性分类
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fast_fast_tle(limit>>1,a1);//分治
    fast_fast_tle(limit>>1,a2);
    complex Wn=complex(cos(2.0*Pi/limit),sin(2.0*Pi/limit)),w=complex(1,0);
    //Wn为单位根，w表示幂
    for(int i=0; i<(limit>>1); i++,w=w*Wn) //这里的w相当于公式中的k
        a[i]=a1[i]+w*a2[i],a[i+(limit>>1)]=a1[i]-w*a2[i];//利用单位根的性质，O(1)得到另一部分
}

时间复杂度：$O(大常数+nlog_2n)$
这个大常数是哪里来的呢？复数运算！实数的乘法是非常慢的。
因此如果不是数据非常大，应尽量避免使用FFT。

点值乘法

经过了FFT的折磨之后呢？
然后直接乘就好了啊。

 fast_fast_tle(n,a);
    fast_fast_tle(n,b);
    for(int i=0;i<=n;i++)
        a[i]=a[i]*b[i];

时间复杂度 $O(n)$。
完了？当然没有。还要逆回去。

快速傅里叶逆变换

设 $(y_0,y_1,...,y_{n-1})$ 是 $(a_0,a_1,a_2,\dots,a_{n-1})$ 的傅里叶变换，即在 $(w_n^0,w_n^1,\dots,w_n^{n-1})$处的值。

则 $y_i=a_0+a_1w_n^1+a_2(w_n^1)^2+\dots +a_n(w_n^1)^n$
$\qquad\,=a_0+a_1w_n^1+a_2w_n^2+\dots +a_nw_n^n$
$\qquad\,=\sum\limits_{j=0}^{n-1}a_j(w_n^i)^j$
设 $(c_0,c_1,c_2,\dots,c_{n-1})$ 是 $(y_0,y_1,...,y_{n-1})$ 在 $(w_n^0,w_n^{-1},\dots,w_n^{-(n-1)})$ 处的取值。
这同样可以用FFT实现，只需要把上面FFT的代码第9行的sin(2.0*Pi/limit)改成-sin(2.0*Pi/limit) 就可以了。
即把单位根变为 $w_n^{-1}$，相当于顺时针旋转。
又到推公式时间了。
即 $c_k=\sum\limits_{i=0}^{n-1}y_i(w_n^{-k})^i$
$\;\qquad=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(w_n^i)^j)(w_n^{-k})^i$
$\;\qquad=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(w_n^j)^i)(w_n^{-k})^i$
$\;\qquad=\sum\limits_{i=0}^{n-1}(\sum\limits_{j=0}^{n-1}a_j(w_n^j)^i(w_n^{-k})^i)$
$\;\qquad=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}a_j(w_n^j)^i(w_n^{-k})^i$
$\;\qquad=\sum\limits_{i=0}^{n-1}\sum\limits_{j=0}^{n-1}a_j(w_n^{j-k})^i$
$\;\qquad=\sum\limits_{j=0}^{n-1}a_j(\sum\limits_{i=0}^{n-1}(w_n^{j-k})^i)$

先 $hold$ 住，来看一看等比数列 $\sum\limits_{i=0}^{n-1}x^i$ 的性质：

---

考虑多项式 $S(x)=(1,1,\dots,1)$，即$S(x)=\sum\limits^n_{i=1}x^i$
将 $x=w_n^k$ 代入得：$S(w_n^k)=1+(w_n^k)+(w_n^k)^2+\dots(w_n^k)^{n-1}\quad(1)$
1. 当 $k\not = 0$ 时，两边同乘$w_n^k$得：

$\quad w_n^kS(w_n^k)=w_n^k+(w_n^k)^2+(w_n^k)^3+\dots(w_n^k)^{n}\quad (2)$

$\quad$然后 $(2)-(1)$ 得
$\quad w_n^kS(w_n^k)-S(w_n^k)=(w_n^k)^{n}-1$

$\,\,\qquad (w_n^k-1)S(w_n^k)=(w_n^k)^{n}-1$

$\quad\therefore\qquad\qquad\, S(w_n^k)=\dfrac{(w_n^k)^{n}-1}{w_n^k-1}$

$\qquad\qquad\qquad\;\;\;\,\qquad=\dfrac{(w_n^n)^{k}-1}{w_n^k-1}$

$\qquad\qquad\qquad\;\;\;\,\qquad=\dfrac{1-1}{w_n^k-1}$

$\qquad\qquad\qquad\;\;\;\,\qquad=0$
2. 当 $k=0$ 时
$S(w_n^k)=1+(w_n^k)+(w_n^k)^2+\dots(w_n^k)^{n-1}$
$\,\;\ \qquad=1+1+1^2+\dots+1^{n-1}$
$\,\;\ \qquad=n$

---

继续考虑刚才的柿子。 $c_k=\sum\limits_{j=0}^{n-1}a_j(\sum\limits_{i=0}^{n-1}(w_n^{j-k})^i)$
1. 当 $j\not=k$ 时，即 $j-k\not=0$，此时 $\sum\limits_{i=0}^{n-1}(w_n^{j-k})^i=0$，共有 $n-1$ 种情况
2. 当 $j=k$ 时，即 $j-k=0$，此时 $\sum\limits_{i=0}^{n-1}(w_n^{j-k})^i=n$，共有 $1$ 种情况。
$\therefore c_k=n\times a_k$

$\therefore \dfrac{c_k}n=a_k$

然后呢？做完啦！
先用 特别的 FFT求出 $(c_0,c_1,c_2,\dots,c_{n-1})$
然后再除以 $n$ 就好啦！
代码有很多重复的部分，因此可以弄多一个参数，表示做的是那一种FFT。
代码

void fast_fast_tle(int limit,complex *a,int type){
    if(limit==1)
        return ;
    complex a1[limit>>1],a2[limit>>1];
    for(int i=0;i<=limit;i+=2)
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fast_fast_tle(limit>>1,a1,type);
    fast_fast_tle(limit>>1,a2,type);
    //当type=1时，表示顺时针的FFT；当type=-1时，表示逆时针的FFT。 
    complex Wn=complex(cos(2.0*Pi/limit),type*sin(2.0*Pi/limit)),w=complex(1,0);
    for(int i=0;i<(limit>>1);i++,w=w*Wn)
        a[i]=a1[i]+w*a2[i],a[i+(limit>>1)]=a1[i]-w*a2[i];
}

执行完后还要处以 $n$，即：

for(int i=1;i<=limit;i++)
    a[i].x/=limit;

时空复杂度分析

令 $N$ 为大于 $n+m$ 的最小的 $2$ 的正整数次幂。
不难看出，FFT的时空复杂度均为 $O(不小的常数+Nlog_2N)$
下面是完整的Luogu P3803代码

#include<cmath>
#include<cstdio>
const int MAXN=2*1e6+10;
const double Pi=acos(-1.0);
struct complex {
    double x,y;
    complex (double xx=0,double yy=0) {
        x=xx,y=yy;
    }
} a[MAXN],b[MAXN];
complex operator+(complex a,complex b) {
    return complex(a.x+b.x,a.y+b.y);
}
complex operator-(complex a,complex b) {
    return complex(a.x-b.x,a.y-b.y);
}
complex operator*(complex a,complex b) {
    return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);
}
void fast_fast_tle(int limit,complex *a,int type){
    if(limit==1)
        return ;
    complex a1[limit>>1],a2[limit>>1];
    for(int i=0;i<=limit;i+=2)
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fast_fast_tle(limit>>1,a1,type);
    fast_fast_tle(limit>>1,a2,type);
    complex Wn=complex(cos(2.0*Pi/limit),type*sin(2.0*Pi/limit)),w=complex(1,0);
    for(int i=0;i<(limit>>1);i++,w=w*Wn)
        a[i]=a1[i]+w*a2[i],a[i+(limit>>1)]=a1[i]-w*a2[i];
}
int main() {
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=0; i<=n; i++)
        scanf("%lf",&a[i].x);
    for(int i=0; i<=m; i++)
        scanf("%lf",&b[i].x);
    int limit=1;
    while(limit<=n+m) limit<<=1;
    fast_fast_tle(limit,a,1);
    fast_fast_tle(limit,b,1);
    for(int i=0; i<=limit; i++)
        a[i]=a[i]*b[i];
    fast_fast_tle(limit,a,-1);
    for(int i=0; i<=n+m; i++)
        printf("%d ",(int)floor(a[i].x/limit+0.5));
        //由于FFT涉及到浮点数运算，因此需要考虑精度误差。
    return 0;
}

$But\ what\ is\ RE?$
注意到空间复杂度中有$O(Nlog_2N)$的空间是开在栈空间里的，因此可能会爆栈！所以有了下一小节。

迭代FFT

定义 $x$ 的 $l$ 位翻转为 $x$ 在 $l-1$ 在二进制位下的长度的翻转。
举个例子：$1$ 的 $8$ 位翻转为 $4$
$8-1$ 的二进制为 $111$，长度为 $3$。
$1$ 的长度为 $3$ 的二进制为 $001$。
前后翻转为 $100$，十进制下即为 $4$

观察一下原下标和新下标的二进制，发现了什么规律？
原下标为 $x$ 的新下标为 $x$ 的 $n-1$ 位翻转。设其为 $r[x]$。
若已经求出了 $r[i]$，则可以写出如下代码：

void fast_fast_tle(complex *A,int type) {
    for(int i=0;i<limit;i++)            //求出要迭代的序列
        if(i<r[i]) swap(A[i],A[r[i]]);
    for(int mid=1;mid<limit;mid<<=1) {  //待合并区间的长度(块的长度)
        complex Wn(cos(Pi/mid),type*sin(Pi/mid));//单位根
        for(int R=mid<<1,j=0;j<limit;j+=R) { //R是区间的右端点，j表示前已经到哪个位置了(枚举那一块)
            complex w(1,0);//幂
            for(int k=0;k<mid;k++,w=w*Wn) { //块内枚举
                complex x=A[j+k],y=w*A[j+mid+k];
                A[j+k]=x+y;
                A[j+mid+k]=x-y;
            }
        }
    }
}

那现在只剩下一个问题了：$r[i]$ 怎么求？

翻转序列

由于FFT的时间复杂度为 $O(Nlog_2N)$。
因此如果求翻转序列的复杂度比 $O(Nlog_2N)$ 还要高那就完了。

暴力

时间复杂度：$O(Nlog_2N)$
空间复杂度：$O(n)$
代码复杂度：$O(小)$
代码：下面的 $l=log_2 limit$，实现上可以在求 $limit$ 的同时求出。

for(int i=1;i<=n-1;i++){
    int t=i,ret=0;
    for(int j=1;j<=l;j++){
        ret=(ret<<1)|(t&1);
        t>>=1;
    }
    r[i]=ret;
}

线性算法

想不到吧，这种东西还有线性算法。
下面以 $184$ 的 $256$ 位翻转为例子。
我们把一个数的二进制分成两部分，设这个数的二进制长度为 $l$ 位。
第一部分是前 $l-1$ 位，第二部分是最后一位。
$\qquad1\quad0\quad1\quad1\quad1\quad0\quad0\quad|\quad0$
$184$ 的 $256$ 位翻转等价于第二部分接上第一部分的 $128$ 位翻转。即
$\qquad0\quad|\quad0\quad0\quad1\quad1\quad1\quad0\quad1$
那第一部分的 $128$ 位翻转怎么求呢？等价于第一部分的 $256$ 位翻转右移 $1$ 位。
第一部分的 $256$ 位翻转
$\qquad0\quad0\quad1\quad1\quad1\quad0\quad1\quad0$
右移一位，得：
$\;\;\quad\qquad0\quad0\quad1\quad1\quad1\quad0\quad1$
代码：

for(int i=1;i<limit;i++)
        r[i]=((r[i>>1]>>1)|((i&1)<<(l-1)));

时间复杂度：$O(n)$
空间复杂度：$O(n)$
代码复杂度：$O(更小)$

最终代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=2148576;
const double pi=acos(-1.0);
struct comp{
    double x,y;
    comp(double xx=0,double yy=0):x(xx),y(yy) {}
    friend comp operator+(const comp &x,const comp &y) {return comp(x.x+y.x,x.y+y.y);}
    friend comp operator-(const comp &x,const comp &y) {return comp(x.x-y.x,x.y-y.y);}
    friend comp operator*(const comp &a,const comp &b) {return comp(a.x*b.x-a.y*b.y,a.x*b.y+b.x*a.y);}
}a[maxn],b[maxn];
int limit=1,n,m,l=0,r[maxn];
void fft(comp *t,int ty){
    for(int i=0;i<limit;i++)
        if(i<r[i])
            swap(t[i],t[r[i]]);
    for(int mid=1;mid<limit;mid<<=1){
        comp wn(cos(pi/mid),ty*sin(pi/mid));
        for(int j=0,R=(mid<<1);j<limit;j+=R){
            comp w(1,0);
            for(int k=0;k<mid;k++,w=w*wn){
                comp x=t[j+k],y=w*t[j+k+mid];
                t[j+k]=x+y;
                t[j+k+mid]=x-y;
            }
        }
    }
}
int main(void)
{
    scanf("%d%d",&n,&m);
    while(limit<=n+m)
        limit<<=1,++l;
    for(int i=1;i<limit;i++)
        r[i]=((r[i>>1]>>1)|((i&1)<<(l-1)));
    for(int i=0;i<=n;++i)
        scanf("%lf",&a[i].x);
    for(int i=0;i<=m;++i)
        scanf("%lf",&b[i].x);
    fft(a,1);
    fft(b,1);
    for(int i=0;i<limit;i++)
        a[i]=a[i]*b[i];
    fft(a,-1);
    for(int i=0;i<=n+m;i++)
        printf("%d ",(int)(a[i].x/limit+0.5));
    return 0;
}

总结

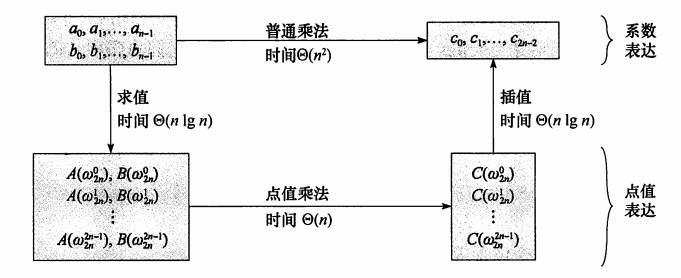
恭喜完成一万字阅读。

题表(坑)

题目	来源	题解
A$\times$B Problem	Luogu 1919	构造
[MUTC2013]idiots	BZOJ3513	容斥原理