无线信道参数估计算法

对通信系统分析之前，首先需要建立一个能够完整反映该系统的传输信道的模型，其模型中的参数包括接收端接收信号的时延，发射端和接收端的联合方向分布等，获取这些参数的过程就是无线信道参数估计的过程。

方法可以大致分为三类：
- 谱估计算法：多重信号分类法
- 参数子空间估计算法：旋转不变技术估计信号参数算法
- 确定性参数估计算法：期望最大算法以及演进的空间交替广义期望最大算法

0. 前言

阵列信号处理基础本质上属于参数估计问题，和信道估计知识基本上别无二致。末学在这里整理了阵列信号处理的基础知识，包括公式推导，以及代码。一方面为了节省同行人士寻找资料和整理吸收的时间，开方便之门。另一方面为了和大家多多交流这方面的知识，寻找研究灵感。

如果有任何问题或者有相关的 MATLAB 代码，本着交流的态度请分享到我的邮箱：[email protected]。

愿以此功德，庄严佛净土。上报四重恩，下济三途苦。
若有见闻者，悉发菩提心。尽此一报身，同生极乐国。

2. 旋转不变性子空间法

ESPRIT 算法原理

基于子空间的 DOA 估计算法包括两大类：MUSIC 类算法及 ESPRIT 类算法。旋转不变性子空间（ESPRIT）类算法和前面讲述的 MUSIC 类算法一样也需要对阵列接收数据协方差矩阵进行特征分解。但两者也有明显的不同点：其中 MUSIC 类算法是利用接收数据协方差矩阵的噪声子空间的正交性，而 ESPRIT 类算法是利用接收数据协方差矩阵的信号子空间的旋转不变性。

与 MUSIC 算法相比，ESPRIT 类算法优点在于计算量小，不需要在空间中不断的进行搜索谱峰。与 ROOT-MUSIC 算法相比，ESPRIT 类算法是利用各子阵的信号子空间之间的旋转不变性求出信号的入射角信息，而 ROOT-MUSIC 算法则是利用导向矢量与噪声子空间的正交性构造多项式并通过对多项式的求解来实现估计。

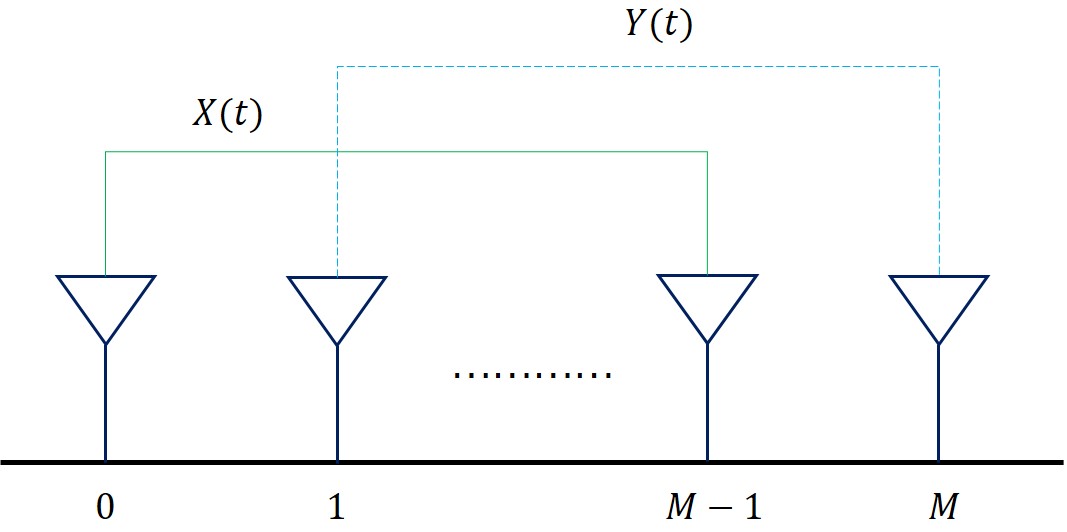
考虑一个有 $M$ 个阵元的平面阵列结构，其元素被恒定位移矢量 $\Delta$ 分离。该阵列由两个完全相同的子阵构成，阵元数目均为 $(M −1)$ 个。其中子阵 1 由前 $(M − 1)$ 个阵元组成，子阵 2 由后 $(M-1)$ 个阵元组成。假设子阵 1 向 $x$ 轴正方向移动 $Δ$ 时与子阵 2 重合。

假设位于远场的具有相同波长的 $d \ (d \leq (M-1))$ 个统计独立的窄带信号 $s_i(t),\ i=1,2,\cdots,d$ ，从方位方向 $\theta_i\ (i=1,2,\cdots,d)$ 入射到阵列。分别用 $X,Y$ 表示子阵 1，2 的接收的来波信号矩阵。子阵 1，2 的输出噪声为 $N_1,N_2$ ，假设它们为零均值且方差为 $\sigma^2$ 的统计独立的高斯白噪声，且与信号矩阵不相关。

则对子阵 1、2 所接收的来波信号矩阵为：

\begin{aligned} X & = A_{1} S + N_{1} \\ = A S + N_{1} \\ = [a (θ_{1}), \dots, a (θ_{d})] {[s_{1} (t), \dots, s_{d} (t)]}^{T} + N_{1} \\ = {[x_{1} (t), x_{2} (t), \dots, x_{M - 1} (t)]}^{T} \\ Y & = A_{2} S + N_{2} \\ = A Φ S + N_{2} \\ = [a (θ_{1}), \dots, a (θ_{d})] diag [e^{j ϕ_{1}}, \dots, e^{j ϕ_{d}}] S + N_{2} \\ = [a (θ_{1}) e^{j ϕ_{1}}, \dots, a (θ_{d}) e^{j ϕ_{d}}] S + N_{2} \\ = {[y_{1} (t), y_{2} (t), \dots, y_{M - 1} (t)]}^{T} \end{aligned}

$\begin{align*} X &= A_1S+N_1 \\ &=AS+N_1 \\ &= \left[a(\theta_1),\cdots,a(\theta_d)\right]\left[s_1(t),\cdots,s_d(t)\right]^T+N_1 \\ &= \left[x_1(t),x_2(t),\cdots,x_{M-1}(t)\right]^T \\ Y &= A_2S+N_2 \\ &=A\Phi S+N_2 \\ &= \left[a(\theta_1),\cdots,a(\theta_d)\right] \text{diag}\left[e^{j\phi_1},\cdots,e^{j\phi_d}\right]S+N_2 \\ &= \left[a(\theta_1)e^{j\phi_1},\cdots,a(\theta_d)e^{j\phi_d}\right] S+N_2 \\ &= \left[y_1(t),y_2(t),\cdots,y_{M-1}(t)\right]^T \end{align*}$

其中， $a(\theta_i) = \left[a_1(\theta_i),\cdots,a_{M-1}(\theta_i)\right]^T$ ， $\Phi$ 为两阵列间的延迟相位， $\phi_i=\frac{2\pi \Delta}{\lambda}\sin \theta_i$ 。由上式可知， $Y$ 是由 $X$ 旋转得到的。因此可以联立两个子阵的模型得到：

\begin{aligned} Z & = [\begin{matrix} X \\ Y \end{matrix}] = [\begin{matrix} A S + N_{1} \\ A Φ S + N_{2} \end{matrix}] \\ = [\begin{matrix} A \\ A Φ \end{matrix}] S + [\begin{matrix} N_{1} \\ N_{2} \end{matrix}] \\ = \bar{A} S + N \end{aligned}

$\begin{align*} Z &=\begin{bmatrix} X \\ Y \end{bmatrix} =\begin{bmatrix} AS+N_1 \\ A\Phi S+N_2 \end{bmatrix} \\ &=\begin{bmatrix} A \\ A\Phi \end{bmatrix}S+\begin{bmatrix} N_1 \\ N_2 \end{bmatrix} \\ &=\bar{A}S+N \end{align*}$
这里可得到协方差矩阵

\begin{aligned} R & = E (Z Z^{H}) \\ = E (\bar{A} S S^{H} {\bar{A}}^{H} + \bar{A} S N^{H} + N S^{H} {\bar{A}}^{H} + N N^{H}) \\ = E (\bar{A} S S^{H} {\bar{A}}^{H} + N N^{H}) \\ = \bar{A} E (S S^{H}) {\bar{A}}^{H} + E (N N^{H}) \\ = \bar{A} R_{S} {\bar{A}}^{H} + R_{N} = \bar{A} R_{S} {\bar{A}}^{H} + σ^{2} I \end{aligned}

$\begin{align*} R &= \mathbb{E}(ZZ^H) \\ &=\mathbb{E}(\bar{A}SS^H\bar{A}^H+\bar{A}SN^H+NS^H\bar{A}^H+NN^H) \\ &=\mathbb{E}(\bar{A}SS^H\bar{A}^H+NN^H) \\ &=\bar{A} \mathbb{E}(SS^H)\bar{A}^H +\mathbb{E}(NN^H) \\ &=\bar{A} R_S\bar{A}^H + R_N = \bar{A} R_S\bar{A}^H + \sigma^2 I \end{align*}$
取

K

$K$ 个时刻的快拍数据，得：

Z (k) = \bar{A} (θ) S (k) + N (k), k = 1, 2, \dots, K

$\boxed{\begin{equation} Z(k)=\bar{A}(\theta)S(k)+N(k),\ \ k=1,2,\cdots,K \end{equation}}$
假设各到达角互不相同，即矩阵

\bar{A}

$\bar A$ 的列向量之间线性独立（ 列满秩）。实际中，只能利用输出采样值估计

R

$R$ ，对协方差矩阵做特征分解：

\begin{aligned} \hat{R} & = \frac{1}{K} \sum_{t = 1}^{K} Z (t) Z (t)^{H}, \\ \hat{R} & = U_{S} Λ_{S} U_{S}^{H} + U_{N} Λ_{N} U_{N}^{H} . \end{aligned}

$\begin{align*} \hat{R} &= \frac{1}{K} \sum_{t=1}^{K}Z(t)Z(t)^H, \\ \hat{R} &= U_S\Lambda_S U_S^H + U_N\Lambda_N U_N^H. \end{align*}$
其中，

Z

$Z$ 的规模是

2 (M - 1) \times 1

$2(M-1)\times 1$ ，因此

\hat{R}

$\hat{R}$ 是

2 (M - 1) \times 2 (M - 1)

$2(M-1)\times 2(M-1)$ 的，

U_{S}

$U_S$ 是

2 (M - 1) \times d

$2(M-1)\times d$ 的。由之前的性质知道

\bar{A}

$\bar{A}$ 与

U_{S}

$U_S$ 张成的子空间一致，则一定存在唯一的非奇异矩阵

T

$T$ ，使得

U_{S} = \bar{A} T

$U_S=\bar AT$ 。则可以分解为

U_{S} = [\begin{matrix} U_{X} \\ U_{Y} \end{matrix}] = [\begin{matrix} A \\ A Φ \end{matrix}] T

$U_S = \begin{bmatrix} U_X \\U_Y \end{bmatrix} =\begin{bmatrix} A \\ A\Phi \end{bmatrix}T$
从上式可立即得到

U_{Y} = A Φ T = U_{X} T^{- 1} Φ T = U_{X} Ψ

$U_Y = A\Phi T = U_X T^{-1}\Phi T = U_X \Psi$ ，其中

Ψ = T^{- 1} Φ T

$\Psi = T^{-1}\Phi T$ 。一旦求出矩阵

Ψ

$\Psi$ ，就可以得到 旋转矩阵：

Φ = T Ψ T^{- 1} = diag [e^{j ϕ_{1}}, \dots, e^{j ϕ_{d}}], ϕ_{i} = \frac{2 π Δ}{λ} \sin θ_{i} ⟹ \hat{θ_{i}} = \arcsin (ϕ_{i} \times \frac{λ}{2 π Δ}) .

$\Phi = T\Psi T^{-1}=\text{diag}\left[e^{j\phi_1},\cdots,e^{j\phi_d}\right],\\ \phi_i=\frac{2\pi \Delta}{\lambda}\sin \theta_i \Longrightarrow \hat{\theta_i} = \arcsin\left( \phi_i \times \frac{\lambda}{2\pi \Delta}\right).$
入射角度就可以通过上面的关系求得。从以上推导可知有如下关键信息：

\begin{aligned} [\begin{matrix} U_{X} \\ U_{Y} \end{matrix}] & = [\begin{matrix} A T \\ A Φ T \end{matrix}] ⟹ \\ span {A} & = span {U_{X}} = span {U_{Y}}, \\ U_{Y} & = U_{X} Ψ ⟹ Ψ = U_{X}^{†} U_{Y} . \end{aligned}

$\begin{align*} \begin{bmatrix} U_X \\U_Y \end{bmatrix} &=\begin{bmatrix} AT \\ A\Phi T \end{bmatrix} \Longrightarrow \\ \text{span}\{A\} &= \text{span}\{U_X\} = \text{span}\{U_Y\}, \\ U_Y &= U_X \Psi \Longrightarrow \Psi = U_X^\dagger U_Y. \end{align*}$
但实际应用中，我们只能得到有限的有噪声的测量数据去估计

span {U_{S}}

$\text{span}\{U_S\}$ ，从而

span {U_{S}} \neq span {\bar{A}}

$\text{span}\{U_S\} \neq \text{span}\{\bar{A}\}$ ，甚至

span {U_{X}} \neq span {U_{Y}}

$\text{span}\{U_X\} \neq \text{span}\{U_Y\}$ 。所以这时我们无法找到

Ψ

$\Psi$ 使得

U_{Y} = U_{X} Ψ

$U_Y = U_X \Psi$ 。必须寻找一个准则以获得

Ψ

$\Psi$ 的合适估计，通常情况下应用的是最小二乘 (LS) 估计。

TLS-ESPRIT 步骤

假设模型 $AX=B$ 中， $A$ 已知且误差由 $B$ 引起，若要获得 $X$ 的估计通常应用标准的 LS 准则。这里容易证明 $A$ 和 $B$ 中同样存在噪声，那么 LS 准则只考虑了 $U_Y$ 的噪声扰动，即 $U_Y+\Delta U_Y = U_X \Psi$ 就是不合适的。

考虑 $A$ 和 $B$ 都有噪声存在的准则是：整体最小二乘法 (TLS)。其思想是同时扰动 $U_Y、U_X$ ，同时矫正 $U_Y、U_X$ 中存在的噪声：

\begin{aligned} (U_{X} + Δ U_{X}) Ψ & = U_{Y} + Δ U_{Y} ⟹ \\ [- U_{Y} - Δ U_{Y}, U_{X} + Δ U_{X}] [\begin{matrix} 1 \\ Ψ \end{matrix}] \\ = ([- Δ U_{Y}, Δ U_{X}] + [- U_{Y}, U_{X}]) [\begin{matrix} 1 \\ Ψ \end{matrix}] \\ = (Δ U + U) z = 0 \end{aligned}

$\begin{align*} \left(U_X+\Delta U_X \right)\Psi &= U_Y+\Delta U_Y \Longrightarrow \\ &\left[-U_Y-\Delta U_Y,U_X+\Delta U_X\right]\begin{bmatrix} 1 \\ \Psi \end{bmatrix} \\ &= \left(\left[-\Delta U_Y,\Delta U_X\right]+\left[-U_Y,U_X\right]\right) \begin{bmatrix} 1 \\ \Psi \end{bmatrix} \\ &= \left(\Delta U+U \right)z=0 \end{align*}$
于是 TLS 的解等价于

min ‖ Δ U ‖^{2} s . t . (Δ U + U) z = 0

$\min \Vert\Delta U\Vert^2 \\ s.t. \quad \left(\Delta U+U \right)z=0$
上面的问题通过下面的最小化问题得到

Ψ

$\Psi$ 的最小二乘解。记

U_{S T} = [U_{X} | U_{Y}]

$U_{ST} = \left[ U_X\vert U_Y\right]$ ，寻找一个酉矩阵

F

$F$ 。上面的 TLS 问题转化为

min ‖ U_{S T} F ‖_{F}^{2} s . t . F^{H} F = I

$\min \Vert U_{ST}F \Vert^2_F \\ s.t. \quad F^HF=I$
我们发现只要使得

F

$F$ 与

U_{X}

$U_X$ 和

U_{Y}

$U_Y$ 都正交即可，则

F

$F$ 可以从

U_{S T}^{H} U_{S T}

$U_{ST}^HU_{ST}$ 的特征分解中得到。因为

\begin{aligned} U_{S T} F & = [U_{X} | U_{Y}] [\begin{matrix} F_{X} \\ F_{Y} \end{matrix}] \\ = A T F_{X} + A Φ T F_{Y} = 0 \\ ⟹ Ψ = - F_{X} F_{Y}^{- 1} \\ U_{S T}^{H} U_{S T} & = E Σ E^{H} \\ = [\begin{matrix} E_{S} & E_{N} \end{matrix}] [\begin{matrix} Λ_{S} \\ Λ_{N} \end{matrix}] [\begin{matrix} E_{S}^{H} \\ E_{N}^{H} \end{matrix}] \end{aligned}

$\begin{align*} U_{ST} F&= \left[ U_X\vert U_Y\right]\begin{bmatrix} F_X \\ F_Y \end{bmatrix}\\ & = ATF_X+A\Phi T F_Y =0\\ & \Longrightarrow \Psi = -F_XF_Y^{-1} \\ U_{ST}^HU_{ST} &= E\Sigma E^H \\ &= \begin{bmatrix} E_S & E_N \end{bmatrix} \begin{bmatrix} \Lambda_S & \\ & \Lambda_N \end{bmatrix} \begin{bmatrix} E_S^H \\ E_N^H \end{bmatrix} \\ \end{align*}$
其中

Σ

$\Sigma$ 是从大到小排列的特征值构成的对角矩阵，由

U_{S T} [w_{1}, w_{2}, \dots, w_{n}] = [w_{1}, w_{2}, \dots, w_{n}] diag (λ)

$U_{ST} \left[ w_1,w_2,\cdots,w_{n}\right]=\left[ w_1,w_2,\cdots,w_{n}\right]\text{diag}(\lambda)$ ，

F

$F$ 应该取后面的噪声子空间

E_{N}

$E_N$ ，对应的

Λ_{N} = 0

$\Lambda_N=\mathbf{0}$ ，可以达到最小化的目的。于是有

F = [\begin{matrix} F_{X} \\ F_{Y} \end{matrix}] = [\begin{matrix} E_{12} \\ E_{22} \end{matrix}] = E_{N}

$F= \begin{bmatrix} F_X \\ F_Y \end{bmatrix} = \begin{bmatrix} E_{12} \\ E_{22} \end{bmatrix} =E_N$
其中，我们对矩阵

E

$E$ 做了划分：

E = [\begin{matrix} E_{11} & E_{12} \\ E_{21} & E_{22} \end{matrix}]

$E = \begin{bmatrix} E_{11}& E_{12} \\ E_{21}& E_{22} \end{bmatrix}$
因此有

Ψ_{T L S} = - F_{X} F_{Y}^{- 1} = - E_{12} E_{22}^{- 1}

$\Psi _{TLS}= -F_XF_Y^{-1} = -E_{12} E_{22}^{-1}$ ，然后求特征值，得到对应的到达角。

ESPRIT 算法仿真

% TLS_ESPRIT ALOGRITHM
% DOA ESTIMATION BY TLS_ESPRIT ALOGRITHM
clear variables;
close all;  clc;

%信噪比(dB)
snr=-10:2:10;
lsnr = length(snr);
RMSE=zeros(1,lsnr);
test_num = 300;

source_number=1; % 信源数
sensor_number=8; % 原阵元数
m=7;             % 子阵元数
N_x=1024;        % 信号长度
snapshot_number=N_x; % 快拍数
w=pi/4;              % 信号频率
l=2*pi*3e8/w;        % 信号波长  
d=0.5*l;             % 阵元间距
array_distance=d;    % 两组阵元轴线方向的间距

source_a= 50;  % 两个信号的入射角度
source_doa= source_a *pi/180;  % 两个信号的入射角度
% 阵列流型
A=[exp(-1i*(0:sensor_number-1)*d*2*pi*sin(source_doa)/l)].';

for isnr = 1:lsnr
    RMSE_i = zeros(1, test_num);
    for iter = 1:test_num
        % 仿真信号
        s=sqrt(10.^(snr(isnr)/10))*exp(1i*w*[0:N_x-1]); 
        %x=awgn(s,snr);
        % 加了高斯白噪声后的阵列接收信号
        x=A*s+(1/sqrt(2))*(randn(sensor_number,N_x)+1i*randn(sensor_number,N_x));
        x1=x(1:m,:);     % 子阵1接受的数据矢量
        x2=x(2:(m+1),:); % 子阵2接受的数据矢量

        % 对两个子阵的模型进行合并
        X = [x1; x2];
        R=X*X'/snapshot_number;
        % 对R进行奇异值分解
        [U,S,V]=svd(R);
        R=R-S(2*m,2*m)*eye(2*m);
        [U,S,V]=svd(R);
        Us=U(:,1:source_number);
        % disp(Us);
        Us1=Us(1:m,:);
        Us2=Us((m+1):2*m,:);
        %Us12=[Us1 Us2];
        % 形成矩阵Us12
        Us12=[Us1,Us2];
        % 对“Us12'*Us12”进行特征分解，得到矩阵E
        [E,Sa,Va]=svd(Us12'*Us12);
        % disp('E');
        % disp(E);
        % disp(Sa);
        % 将 E_4x4 分解为四个小矩阵
        E11=E(1,1);
        E12=E(1,2);
        E21=E(2,1);
        E22=E(2,2);
        % 按照公式得到旋转不变矩阵M
        M=-(E12*(inv(E22)));
        % disp('M');
        % disp(M);
        % 对得到的旋转不变矩阵进行特征分解
        [Vm,Dm]=eig(M);
        % disp(Dm);
        Dm=(diag(Dm)).';
        doa=-asin(angle(Dm)/pi)*180/pi;
        disp(doa);
        RMSE_i(iter)=sqrt((doa-source_a)^2);
    end
    RMSE(isnr) = sum(RMSE_i)/test_num;
end

%% plot 
figure;
plot(snr,RMSE,'m-s');
%legend('elevation','azimuth');
xlabel('SNR (dB)');
ylabel('RMSE of(degree)');
%axis([-100 100 -40 60]);
%set(gca, 'XTick',[-100:20:100]);
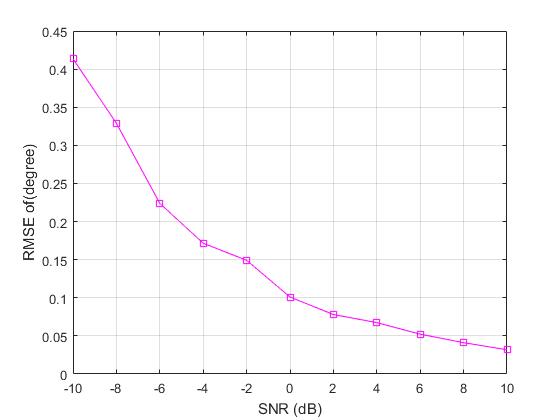
grid on;

运行效果如图：

esp

阵列信号基础之2：ESPRIT 算法