特征值和特征向量，PCA算法

第一部分：线性变换与特征值和特征向量之间的关系

线性变换

线性变换的定义：设V为线性空间，如果存在一个从V到V自身的对应法则 $\sigma$，使得对任意 $\alpha\in V$，有唯一的V中的元素（记为 $\sigma(\alpha)$）与之对应，而且 $\sigma$满足：
(1) 对任意 $\alpha,\beta \in V$，有 $\sigma(\alpha + \beta) = \sigma(\alpha) + \sigma(\beta)$。
(2) 对任意 $\alpha\in V$及 $\lambda \in R$，有 $\sigma(\lambda \alpha) = \lambda \sigma(\alpha)$。
则称 $\sigma$为线性空间V的一个线性变换， $\sigma(\alpha)$称为 $\alpha$的像， $\alpha$称为 $\sigma(\alpha)$的原像。

线性变换可以用方阵来表示，下面我们举几个例子：
例1：方阵 $\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}$将所有的（二维）向量都线性变换到它自身。即
$\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}\alpha = \alpha$

例2：方阵 $\begin{matrix} 0 & -1 \\ 1 & 0 \end{matrix}$将所有的（二维）向量都逆时针旋转90 度。（该方阵的特征值是 $\pm i$，不是实数的例子。）

例3：方阵 $\begin{matrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{matrix}$将所有的（二维）向量都逆时针旋转 $\theta$ 度。

例4：针对x轴反射： $\begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix}$

例5：在所有方向上放大2 倍： $\begin{matrix} 2 & 0 \\ 0 & 2 \end{matrix}$

例6：垂直错切： $\begin{matrix} 1 & m \\ 0 & 1 \end{matrix}$

例7：挤压： $\begin{matrix} k & 0 \\ 0 & 1/k \end{matrix}$

例8：向y轴投影： $\begin{matrix} 0 & 0 \\ 0 & 1 \end{matrix}$

对于线性变换我们有以下的结论：线性变换是在某些方向上做伸缩操作（特征值是实数）；或者沿着某些方向做旋转操作（特征值是虚数）。所以线性变换由“方向”和“比例”来决定。

特征值和特征向量的定义

先看方阵的特征值和特征向量的定义：

设A是n阶方阵，如果数λ和n维非零列向量α使关系式
$Aα = λα$
成立，则数λ称为矩阵A的特征值，非零向量α称为A的对应于特征值λ的特征向量。

这个关系式的意义是什么呢？

如第一节所述，线性变换可以用方阵来表示，如果我们将上面的方阵A看作一个线性变换，则上述关系式的意义是：该线性变换将其特征向量 $\alpha$保持方向不变，而将其长度伸缩 $\lambda$倍（ $\lambda$是实数的情形，如果 $\lambda$是虚数，则是旋转操作）。

对角阵的特征值和特征变量

我们举几个例子来考察一下对角阵的特征值和特征变量的性质。

例1

单位矩阵 $\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}$
由特征方程
$\begin{vmatrix} \lambda-1 & 0 \\ 0 & \lambda-1 \end{vmatrix} = 0$
得特征值 $\lambda_1=\lambda_2=1$
由方程
$(A-\lambda E) X= 0$
得任意向量都是该矩阵的特征向量。
实际上，单位矩阵 $\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}$所表示的线性变换为恒等变换，也就是说，它把所有的向量都变换为该向量本身。这跟我们所得到的关于该矩阵的特征值和特征向量的性质的结论是一致的。

例2

对角阵 $\begin{matrix} 1 & 0 \\ 0 & 3 \end{matrix}$
由特征方程
$\begin{vmatrix} \lambda-1 & 0 \\ 0 & \lambda-3 \end{vmatrix} = 0$
得特征值 $\lambda_1=1，\lambda_2=3$
将 $\lambda_1=1$带入方程
$(A-\lambda E) X= 0$
得到其特征向量是 $k\begin{vmatrix} 1 \\ 0 \end{vmatrix}$，也就是说，该矩阵所表示的线性变换将所有x轴上的向量都做恒等变换。
将 $\lambda_2=3$带入方程
$(A-\lambda E) X= 0$
得到其特征向量是 $k\begin{vmatrix} 0 \\ 1 \end{vmatrix}$，也就是说，该矩阵所表示的线性变换将所有y轴上的向量都加长3倍。
对于其它的任意向量，则保持其x轴上的长度不变，y轴上的长度都加长3倍。

例3

对角阵 $\begin{matrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{matrix}$
通过与上面完全类似的计算可以得到该矩阵的特征值为 $\lambda_1=1，\lambda_2=\lambda_3=3$
对应特征值 $\lambda_1=1$的特征向量是 $k\begin{vmatrix} 1 \\ 0 \\ 0 \end{vmatrix}$，也就是说，该矩阵所表示的线性变换将所有x轴上的向量都做恒等变换。
对应特征值 $\lambda_2=\lambda_3=3$的两个线性无关的特征向量是 $k\begin{vmatrix} 0 \\ 1 \\ 0 \end{vmatrix}和k\begin{vmatrix} 0 \\ 0 \\ 1 \end{vmatrix}$，根据特征向量的性质，所有的向量 $k_1\begin{vmatrix} 0 \\ 1 \\ 0 \end{vmatrix}+k_2\begin{vmatrix} 0 \\ 0 \\ 1 \end{vmatrix}$都是其特征向量，也就是说，该矩阵所表示的线性变换将所有与x轴垂直的平面上的向量都加长3倍。

关于对角阵的特征值和特征向量，我们有以下的重要结论：对角阵的特征向量都是沿着基的方向。

实对称矩阵的特征值和特征向量的性质

例1

实对称矩阵A= $\begin{matrix} 1 & 1 \\ 1 & 1 \end{matrix}$
的特征值是 $\lambda_1=0，\lambda_2=2$
特征值 $\lambda_1=0$对应的特征向量是k $\begin{matrix} 1 \\ -1 \end{matrix}$，特征值 $\lambda_1=2$对应的特征向量是k $\begin{matrix} 1 \\ 1 \end{matrix}$
也就是说，该实对称矩阵将所有的向量k $\begin{matrix} 1 \\ -1 \end{matrix}$（与x轴成145^∘角的向量）都线性变换为0向量，将所有的向量k $\begin{matrix} 1 \\ 1 \end{matrix}$（与x轴成45^∘角的向量）都加长2倍。

而对于任意的向量，该线性变换将它在与x轴成145^∘角的方向上的分量都清零，将它在与x轴成45^∘角的方向上的分量都加长2倍。

例2

实对称矩阵 $\begin{matrix} 1 & 2 \\ 2 & 1 \end{matrix}$
的特征值是 $\lambda_1=3，\lambda_2=-1$
特征值 $\lambda_1=3$对应的特征向量是k $\begin{matrix} 1 \\ 1 \end{matrix}$，特征值 $\lambda_1=-1$对应的特征向量是k $\begin{matrix} 1 \\ -1 \end{matrix}$
也就是说，该实对称矩阵将所有的向量k $\begin{matrix} 1 \\ 1 \end{matrix}$（与x轴成45^∘角的向量）都加长3倍，将所有的向量k $\begin{matrix} 1 \\ -1 \end{matrix}$（与x轴成145^∘角的向量）都反转方向且保持长度不变。

而对于任意的向量，该线性变换将它在与x轴成45^∘角的方向上的分量都加长3倍，将它在与x轴成145^∘角的方向上的分量都反转方向且保持长度不变。

到此我们已经可以得出关于线性变换与特征值和特征向量之间的关系的重要结论，即下面的谱定理：
Spectral Theorem:一个线性变换（用矩阵乘法表示）可表示为它的所有的特征向量的一个线性组合，其中的线性系数就是每一个向量对应的特征值。写成公式就是：
$T(v) = \lambda_1(v1\cdot v)v_1 + \lambda_2(v2\cdot v)v_2 + ...$

以下是关于实对称矩阵的特征值和特征向量的结论：

1. 实对称矩阵的特征值都是实数，特征向量都是实向量。
2. 实对称矩阵的不同特征值对应的特征向量是正交的。
3. n阶实对称矩阵A的一个k重的特征值 $\lambda$必有k个线性无关的特征向量。或者说必有秩 $r(\lambda E-A)=n-k$

相似矩阵

方阵相似的定义如下：
设A，B都是n阶方阵，若存在可逆矩阵P，使
$P^{-1}AP = B$
则称B是A的相似矩阵，或者说矩阵A与B相似。P称为把A变成B的相似变换矩阵。

相似矩阵的几何意义是：
如果一个线性变换在两组不同的基下的矩阵分别是A和B，则A和B相似。

以下是关于实对称矩阵的相似矩阵的结论：

实对称矩阵必与一个对角阵相似，并且相似对角阵上的元素即为矩阵本身的特征值，相似变换矩阵P是由所有线性无关的特征向量组成的。

第二部分：数据矩阵与特征值和特征向量之间的关系

特征值分解

一个方阵可以分解为下面的形式：
$A = Q\Sigma Q^{-1}$
其中Q是这个矩阵A的特征向量组成的矩阵， $\Sigma$是一个对角阵，每个对角线上的元素就是一个特征值。

奇异值分解(SVD)

对于任意的mn矩阵来说，则可以分解为以下的形式：
$A = U\Sigma V^{T}$
假设A是一个mn的矩阵，则得到的U是一个mm的方阵（里面的向量是正交的，称为左奇异向量）， $\Sigma$是一个mn的矩阵（除了对角线上的元素外都是0，对角线上的元素称为奇异值）， $V^T$是一个n*n的方阵（里面的向量是正交的，称为右奇异向量）。
那么奇异值，左奇异向量和右奇异向量是怎么得到的呢？
首先我们计算 $A^TA$（它是一个方阵）的特征值和特征向量：
$(A^TA)V_i = \lambda_iv_i$
这里得到的v就是上面的右奇异向量。接着我们计算：
$\sigma_i = \sqrt{\lambda_i}$
$u_i = \frac{1}{\sigma_i}Av_i$
这里的 $\sigma$就是奇异值，u就是左奇异向量。
奇异值 $\sigma$跟特征值类似，在矩阵 $\Sigma$中也是从大到小排列，而且 $\sigma$的减少特别的快，在很多情况下，前10%甚至1%的奇异值之和就占了全部奇异值之和的99%以上了。也就是说，我们可以用前r大的奇异值来近似第描述矩阵，这就是部分奇异值分解：
$A_{m*n}\approx U_{m*r}\Sigma_{r*r}V^T_{r*n}$
这里r要远小于m和n，右边的三个矩阵相乘的结果将会是一个接近于A的矩阵。r越接近于n，则相乘的结果越接近于A。而这三个矩阵的数据量之和要远远小于原始的矩阵A，我们如果想要压缩空间来表示原矩阵A，我们存下这里的三个矩阵：U、Σ、V就好了。
这里需要指出，奇异值的计算是一个难题，它是一个 $O(N^3)$的算法，在单机情况下，matlab在一秒钟内就可以算出1000 * 1000的矩阵的所有奇异值，但是当矩阵的规模增长的时候，计算的复杂度呈3次方增长，就需要并行计算参与了。目前已经有算法解决了这个难题。

第三部分：主成分分析（PCA-Principle Component Analysis）

在实际问题中往往需要研究很多个特征，而这些特征存在一定的相关性。主成分分析（PCA）的思路是，将多个特征综合为少数几个有代表性的特征，它们既能够代表原始特征的绝大多数信息，组合后的特征又不相关。这样，我们通过减少特征的数量（即降维）达到了降低问题复杂性，又尽可能少地减少数据的特征损失的目的，这就是主成分分析（PCA）。
那么我们怎么提取数据的“主成分”呢？
假定我们采集到下图所示的原始数据。

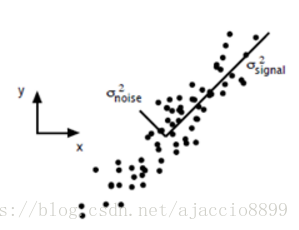
为了寻找样本的主方向，将所有的m个样本投影到某直线L上，得到m个位于直线L上的点，计算这m个投影点的方差，我们认为方差最大的直线方向是主方向。
（一般来说，方差大的方向是信号的方向，方差小的方向是噪声的方向，我们在数据挖掘中或者数字信号处理中，往往要提高信号与噪声的比例，也就是信噪比。对上图来说，如果我们只保留signal方向的数据，也可以对原数据进行不错的近似了。这也就是“降噪”的原理。）
PCA的全部工作简单点说，就是在原始的空间中顺序地找一组相互正交的坐标轴，第一个轴是使得方差最大的，第二个轴是在与第一个轴正交的平面中使得方差最大的，第三个轴是在与第1、2个轴正交的平面中方差最大的，这样假设在N维空间中，我们可以找到N个这样的坐标轴，我们取前r个去近似这个空间，就可以提取数据的前r个“主成分”了。

补充知识：矩阵与向量的乘积的几何意义

设矩阵
$A = \begin{matrix} a_{11} & a_{12} &... & a_{1n} \\ a_{21} & a_{22} &... & a_{2n} \\ ...\\ a_{m1} & a_{m2} &... & a_{mn} \end{matrix}$
矩阵可以看作是一个向量，该向量中的每一个元素又都是向量。即
$A = \begin{matrix} \alpha_1\\ \alpha_2 \\ ...\\ \alpha_m \end{matrix}$
其中
$\alpha_1 = (a_{11}, a_{12},... , a_{1n} )$
$\alpha_2 = (a_{21}, a_{22},... , a_{2n} )$
$...$
$\alpha_m = (a_{m1}, a_{m2},... , a_{mn} )$
所以，对于向量u
$Au = \begin{matrix} \alpha_1\\ \alpha_2 \\ ...\\ \alpha_m \end{matrix}u = \begin{matrix} \alpha_1 u\\ \alpha_2 u\\ ...\\ \alpha_m u \end{matrix}$

假定u是单位向量，则上述Au的结果是一个向量，其中的每一个分量 $\alpha_iu$是向量 $\alpha_i$在向量u方向上的投影的长度。这就是矩阵与向量的乘积的几何意义。

PCA的推导

我们的任务在于，对于一个有m个样本，每个样本有n个特征的数据组成的矩阵：

$A = \begin{matrix} a_{11} & a_{12} &... & a_{1n} \\ a_{21} & a_{22} &... & a_{2n} \\ ...\\ a_{m1} & a_{m2} &... & a_{mn} \end{matrix}$
要找到一个投影直线L，使得所有的数据投影到该直线上的方差最小。
设投影直线L方向上的单位向量为u，则根据上面的补充知识，Au这个向量的各个分量就是m个样本在L方向上的投影的长度。假定m个样本事先是去均值的，则向量Au的方差
$Var(Au) = (Au-E)^T(Au-E)=(Au)^T(Au)=u^TA^TAu$
所以目标函数
$J(u) = u^TA^TAu$
我们要求J(u)的最大值，约束条件为u是单位向量，即 $\begin{Vmatrix}u\end{Vmatrix}_2=1$，也就是 $u^Tu=1$。
求约束条件下的极值问题，我们直接用拉格朗日公式：
$L(u) = u^TA^TAu - \lambda(u^Tu-1)$
对其求u的导数：
$\frac{dL(u)}{du}=A^TAu-\lambda u$
令其为0，得到
$A^TAu=\lambda u$
由于 $A^TA$是一个方阵，所以上式的含义就是，u是方阵 $A^TA$的特征向量， $\lambda$是方阵 $A^TA$的特征值（它就是转置到u方向之后的方差）。
由于 $A^TA$与A的协方差矩阵只相差一个系数n-1，所以上述问题转化为求A的协方差矩阵的特征向量和特征值。
求出A的协方差矩阵（实对称阵）的特征向量和特征值之后，就可以用特征值分解的方法进行降维了。