一、特征向量
对于某个矩阵$A$,如果有$Ax=\lambda x$,则$x$是矩阵$A$的特征向量,$\lambda$是矩阵$A$的特征值,矩阵$A$可以作用于任何向量$x$,但我们感兴趣的是那些$x$向量,$Ax$之后的结果和$x$同向(平行于$x$),$\lambda$可以取0或者负值
解释:矩阵$A$作用于某向量$x$之后的结果(向量)与向量$x$同向(所谓同向就是平行,即可以方向相反),那么这些$x$就是矩阵$A$的特征向量
注意:如果矩阵$A$是不可逆矩阵,行或者列线性相关(咱先比如列线性相关),则肯定存在$Ax=0$的$x$向量($x$为相关性系数),即$A$可以把某个非零向量转化为零向量,那么$\lambda = 0$是一个特征值,但应该还有其他特征值
二、如何求得这些$x$和$\lambda$呢?
$Ax=\lambda x$,存在两个未知数,不像$Ax=b$方程只有一个未知数,所以不能用消元法求两个未知数
我们之前讲过投影矩阵,作用于$b$,可以将$b$投影于列空间内,那么投影矩阵的$x$和$lambda$是什么呢?
对于投影矩阵:$P$作用于$b$得到$p$,即$Pb=p$,但是$b$和$p$不同向,所以$b$不是投影矩阵的特征向量
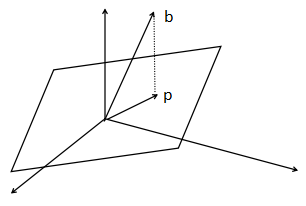
那么哪些$b$经过投影后得到的投影向量$p$,即哪些向量本身和自己的投影在相同的方向上呢?那就是正好落在平面上的向量,那么任意平面上的向量就是一个特征向量。
我们假设这个任意平面上的向量为$x$,经过投影后结果还是$x$,$Px=x$,那么此时$\lambda = 1$,如果$x$垂直于平面,经过投影后结果为0,即$Px=0$,则此时$\lambda = 0$
三、置换矩阵的特征值和特征向量
如:$A=\left[\begin{array}{ll}{0} & {1} \\ {1} & {0}\end{array}\right]$
$X=\left[\begin{array}{ll}{1} \\ {1}\end{array}\right]$,$\lambda=1$为一组
$X=\left[\begin{array}{ll}{-1} \\ {1}\end{array}\right]$,$\lambda=-1$为一组
四、特征值之和
矩阵$A$的特征值之和等于对角元素之和
五、求解特征值和特征向量
$Ax=\lambda x$ 推出$(A - \lambda I)x=0$,如果$x$有非零解,$(A - \lambda I)$一定是奇异的,$|A - \lambda I | = 0$,叫做特征方程
在三中,我们知道$A_1=\left[\begin{array}{ll}{0} & {1} \\ {1} & {0}\end{array}\right]$,则
$\lambda_1=1, X_1=\left[\begin{array}{ll}{1} \\ {1}\end{array}\right]$
$\lambda_2=-1, X_2=\left[\begin{array}{ll}{-1} \\ {1}\end{array}\right]$
我们现在看另外一个例子:$A_2=\left[\begin{array}{ll}{3} & {1} \\ {1} & {3}\end{array}\right]$,则
$|A - \lambda I | = \left|\begin{array}{ll}{3-\lambda} & {1} \\ {1} & {3-\lambda}\end{array}\right|=(3-\lambda)^2 - 1=\lambda ^ 2 - 6\lambda + 8$
其中6代表“迹”,8代表$A$的行列式
$\lambda_1=4, X_1=\left[\begin{array}{ll}{1} \\ {1}\end{array}\right]$
$\lambda_2=2, X_2=\left[\begin{array}{ll}{-1} \\ {1}\end{array}\right]$
通过对比发现:$A_2$比$A_1$增加了$3I$,即$A_1 + 3I = A_2$,相应的特征值也增加3,特征向量不变,即:
如果$Ax=\lambda x$,则$(A+3I)x=(\lambda + 3)x$,$x$为两个矩阵共同的特征向量
但这里要注意:如果$Ax=\lambda x$(知道$A$的特征值和特征向量),$B$有特征值$\alpha$,$(A+B)x=(\lambda + \alpha)x$不一定成立,只有$B=\alpha I$时才成立,因为$Ax$与$Bx$中的$x$不一定相同
六、旋转矩阵
90度的旋转矩阵:
$Q = \left[\begin{array}{ll}{cos \theta} & {-sin \theta} \\ {sin \theta} & {cos \theta}\end{array}\right]=\left[\begin{array}{ll}{0} & {-1} \\ {1} & {0}\end{array}\right]$
特征值之和,“迹”为0
特征值之积等于行列式
$det(Q-\lambda I) = \left|\begin{array}{ll}{-\lambda} & {-1} \\ {1} & {-\lambda}\end{array}\right|=\lambda^2 + 1=0$,那么$\lambda$不是实数
七、致谢
本文参考,感谢作者分享,知识共享,改变世界!