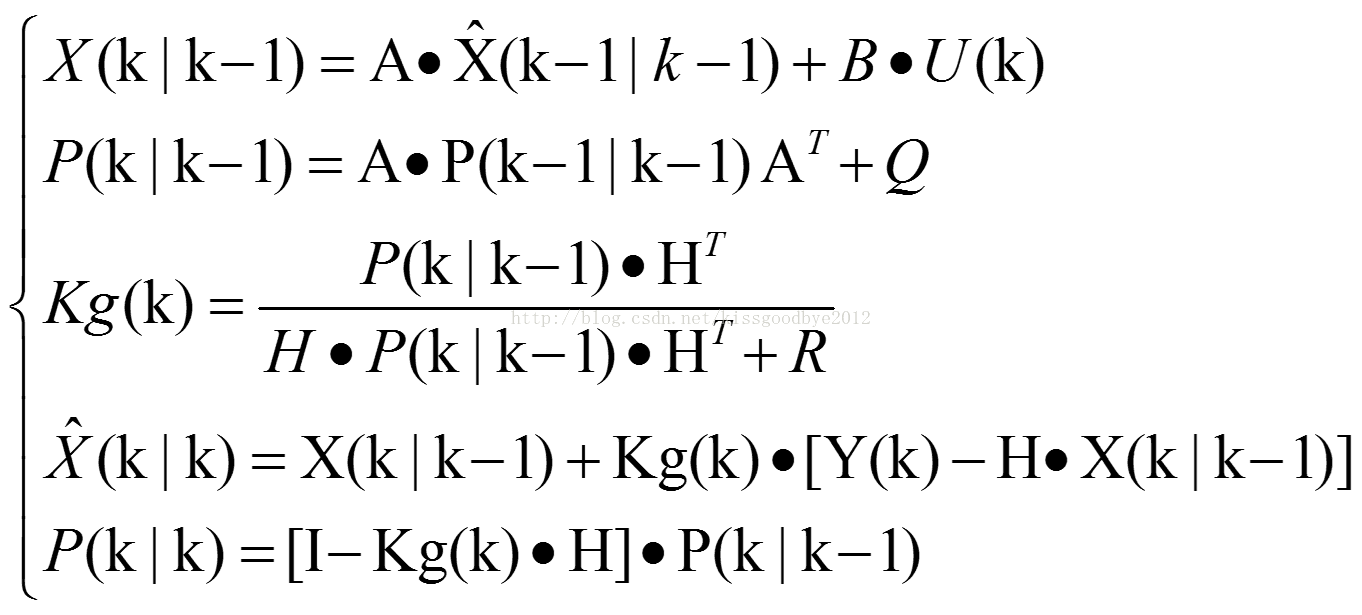前言:在看了R.E.Kalman关于线性滤波器的原文,以及网上关于Kalman滤波器的各种解释后,我来写写我理解的Kalman滤波器及工程上怎么应用它!
Kalman滤波器通俗解释:这个滤波器其实相当于一个信息融合方法。
我现在要知道时刻k系统的状态X(k),我可以建立一个模型,这个模型根据时刻k-1系统的状态估算出时刻k系统的状态X(k),当然这个状态并不准确(假定我们建立不了那么准确的模型,除非真的特别牛,建了一个特别厉害的模型!),我们假设估算得到的这个系统状态X(k)存在误差,服从高斯分布,也就是正态分布,且均值为0;
除了建立模型,我也可以利用传感器直接测量当前的状态,得到另一个时刻k系统的状态X(k),当然传感器也存在误差,我们假设它的误差也服从高斯分布,也就是正态分布,且均值为0;
重点:我们现在得到了两个或多个对系统时刻k的状态估计,那么怎么融合这些信息,得出最佳估计呢?答案是:将所有估计进行加权平均(是不是觉得怎么这么简单?对,难的是怎么确定这些权重)
首先讲怎么用Kalman滤波器:
你的系统需要是一个离散的控制过程系统——线性系统,不论是数学模型还是观测模型!(可忽略,反正只要公式形式和原理上差不多就行),可以建立如下的模型:
我先来解释一波:
(1)A,B,H都是你建立的数学模型和测量模型的参数,对任意时刻都是一样的。如果是多模型则A,B为矩阵,如果是多测量系统则H为矩阵;
—————:一般H比较难理解,就比如你要测环境的温度X(k),但实际你观测到的可能是输出的电压,输出的电流,这个电压和电流与温度之间是一个比例关系,也就是这里的H矩阵了!又比如你要测速度X(k),但观测到的是位移,又知道两个时刻k和k-1之间的时间差,于是这之间又有一个比例关系,这就是H矩阵!反正重点是:H矩阵代表状态X(k)如何转移成观测Y(k)!
(2)U(k)为时刻k的线性系统输入;
(3)w(k)~N(0,Q)和v(k)~N(0,R)都是服从均值为0的高斯分布(正态分布),他们的方差分别为Q(对应w(k))和R(对应v(k)),我们假定他俩的方差不会随时间改变(Q和R为定值);
放5个公式(核心):
看懂这五个公式了吗?不懂我下面会慢慢解释,会这五个公式,再加上一点初始条件的设置,你就可以用Kalman滤波了,开心吗?至于具体的原理,为什么是这个公式,如果想知道,请继续看下去,否则看懂这五个公式就足够了!(编程起来非常简单……)
1.基于数学模型进行预测:
解释一下:
(1)X(k|k-1)代表从k-1时刻估计的时刻k的状态;
(2)头上带尖角的说明它是最佳的估计值;
(3)头右上角的T说明是矩阵的转置(这个不会不知道吧);
(4)P(k|k-1)是最小均方误差矩阵;
(5)Q为数学模型预测的方差;
2.修正估计值:
解释一下:
(1)Kg(k)为卡尔曼增益(误差增益);
(2)R为观测模型误差的方差;
3.最小均方误差矩阵的更新
解释一下:
(1)I为单位阵(错看成1也没关系,本来就是一串对角1);
4.初始条件的设定
我们需要的初始条件有:
(1)首先那些系统参数你要知道:A,B,H,Q,R;
(2)时刻0的状态X(0|0)和P(0|0),这个没有先验条件下可以随便设,但是P(0|0)最好不要设为0,看公式就知道这样P就不能更新了,只会为0(物理意义上就认为X(0|0)最优);
5.总述说明
(1)设置好初始条件,根据五个公式就可以不断迭代下去,算法最终会收敛的,也就是越来越准!(这个可是当年Kalman发论文的核心——我证明了我的这个是最好的,算法最终会收敛!傲娇脸~~),想看证明的我之后会更新!
(2)其实Kalman滤波的关键就是那个Kg,他利用方差来判断相信数学模型还是观测模型多一点(这里涉及统计观点,所以学好概率论是多么重要!)。
Kalman滤波实际中存在的困难:
1.Kalman滤波发散
(1)很多时候两个方差P和R我们并不知道,或者本身P和R会随着时间变化;
(2)很多时候系统参数我们都不知道A,B,H;
………………………………写于2017年4月6日